ProdukČní funkce a mezní produkt
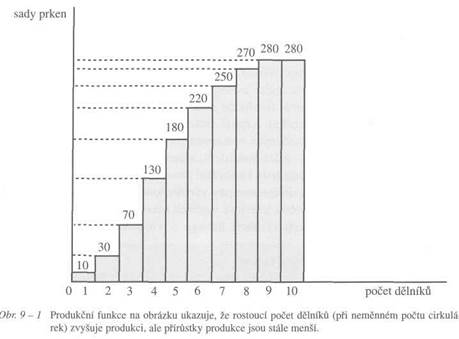
Produkční funkci jste poznali už ve 3. kapitole. Nyní se k ní vrátíme. Na obrázku 9-1 vidíte produkční funkci - funkci celkového produktu Součkovy pily, kdy dělníci jsou variabilním výrobním faktorem. Tvar křivky je dán působením zákona klesajících výnosů z variabilního faktoru.
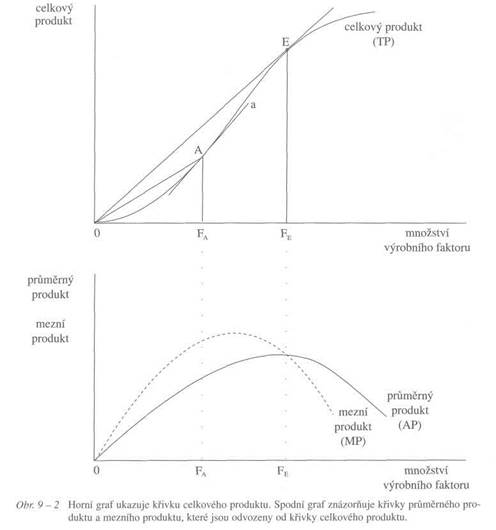
Funkce celkového produktu (TP) popisuje závislost celkového produktu na množství variabilního výrobního faktoru. Z funkce celkového produktu lze odvodit funkci průměrného produktu (průměrné produktivity) a funkci mezního produktu (mezní produktivity) výrobního faktoru.
Průměrný produkt výrobního faktoru (AP) získáme, když dělíme celkový produkt počtem jednotek výrobního faktoru.
Mezní produkt výrobního faktoru (MP) je přírůstek produkce, dosažený zvýšením daného faktoru o jednotku, při ostatních faktorech nezměněných.
|
|
| Produkční funkce a mezní produkt |
Obrázek 9-2 ukazuje odvození křivek průměrného produktu a mezního produktu určitého výrobního faktoru (při ostatních faktorech neměnných) z křivky celkového produktu. Na horním grafu je křivka celkového produktu. Jaký je průměrný produkt například v bodě A? Získáme jej jako podíl celkového produktu a množství výrobního faktoru. Celkový produkt je dán úsečkou AFA a množství výrobního faktoru je dáno úsečkou OFA. Průměrný produkt je tedy dán podílem AFA: OFA, čili sklonem úsečky OA (tangentou úhlu, který úsečka OA svírá s vodorovnou osou).
Jak velký je mezní produkt v bodě A? Při velmi malých jednotkách výrobního faktoru je mezní produkt dán sklonem tečny a ke křivce celkového produktu v bodě A.
Získané hodnoty průměrného a mezního produktu přenášíme na spodní graf obrázku. V bodě A je mezní produkt větší než průměrný produkt, protože sklon tečny a je

 Poptávka po výrobních faktorech
Poptávka po výrobních faktorech
větší než sklon úsečky OA. Nyní se podívejme na bod E. V tomto bodě je úsečka OE, znázorňující průměrný produkt, totožná s tečnou, znázorňující mezní produkt - neboli v bodě E je průměrný produkt stejný jako mezní produkt. Zároveň vidíme, že až do bodu E průměrný produkt roste a za tímto bodem začíná klesat. To znamená, že funkce průměrného a mezního produktu se protínají v bodě maxima průměrného produktu, jak to také vidíte na spodním grafu.
Nakonec si připomeňme, že produkční funkce byla zkonstruována za předpokladu ostatních výrobních faktorů neměnných. Kdyby se některý z ostatních faktorů zvětšil, vedlo by to ke zvýšení produkce a křivka celkového produktu na horním grafu i křivky průměrného a mezního produktu na dolním grafu by se posunuly vzhůru.
Musíme tedy odlišovat pohyb podél produkční funkce, k němuž dochází při zvětšování sledovaného variabilního faktoru (při ostatních faktorech neměnných), od posu nu produkční funkce, k němuž dochází při změně ostatních výrobních faktorů.