Метод парных сравнений
Московский государственный университет имени М. В. Ломоносова
Факультет психологии
Кафедра методологии психологии
Общий психологический практикум
Отчет на тему: «Метод парных сравнений»
Выполнила:
студентка 3-го курса
вечернего отделения
21 группы
Реутова А.П.
Преподаватель:
Сагова З.А.
Москва, 13 февраля 2013 г.
Метод парных сравнений
Метод парных сравнений основан на попарном сравнении альтернатив. Для каждой пары альтернатив эксперт указывает, какая из альтернатив предпочтительнее (лучше, важнее и т.д.). Существует ряд алгоритмов, реализующих метод парных сравнений: они различаются по количеству используемых экспертных оценок (индивидуальные и коллективные оценки), по шкалам сравнения альтернатив и т.д. Ниже рассматриваются два алгоритма, реализующие метод парных сравнений.
Каждое сравнение производится много раз. На основании этих сравнений для каждой пары определяется частота предпочтения одного стимула другому. Квадратная матрица частот представляет исходные данные
Последующий анализ заключается в переходе от матрицы частот к матрице вероятностей. Элемент этой матрицы,есть пропорция числа предпочтений i-го стимула j-му в общем числе сравнений этих двух стимулов.
Из матрицы вероятностей уже легко определить матрицу различий значение zi,j для соответствующей вероятности можно определить по таблице областей под единичной нормальной кривой. Для практического удобства матрицу Z следует перестроить таким образом, чтобы столбцы были упорядочены по величине.
Из матрицы Z' можно получить матрицу различий D между соседними парами столбцов, вычитая их поэлементно один из другого. В каждой j-й строке элемент этой матрицы будет равен (zj,i+1 - zj,i).
Далее (опуская некоторые нюанс которые будут подробно раскрыты ниже) вычисляем из полученных различий шкальные значения стимулов.
Цели и гипотезы
Цели:
1. Учебная цель задания является освоение метода парных сравнений.
3. Научиться преобразовывать, а главное понимать значение матриц.
2. Построение интервальной шкалы.
Методика исследования
Мы индивидуально работали с компьютерной программой для определения в данной работе расположения стимулов в некотором континууме, в данном случае по теплоте цвета. Затем мы объединялись в пары или тройки, усредняли значения матриц и далее работали с ними.
Стимульный материал: пары цветных квадратов.
Оборудование: Компьютер, предъявляющая стимулы программа.
Инструкция: Задача в каждом случае - выбрать наиболее теплый цвет из двух предъявляемых. Нажмите клавишу "=>", если правый цвет более теплый, нажмите клавишу "<=", если левый цвет более теплый.
Каждая пара будет предъявляться по 5 раз в случайном порядке, отвечать следует как можно быстрее, по первому ощущению.
Далее мы составляем матрицу частот F, элементом матрицы является частота, с которой в паре j,i стимул i оценивался более теплым, чем стимул j. Её следует усреднить с партнером по заданию. Количество номеров соответствует количеству стимулов.
После преобразуем матрицу F в матрицу вероятностей P путем деления каждого элемента на число предъявлений. Такая матрица отображает вероятность предпочтения каждого элемента.
Каждое значение вероятности из матрицы Р переводится далее с помощью таблицы в единицы стандартного отклонения нормальной кривой — zi,j, матрицы Z. Сразу выполняем преобразование в матрицу Z` оценок путем упорядочивания столбцов по возрастанию суммы. Заметим что Для вероятностей = 0 или 1 z не существет.
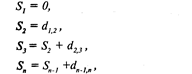Наконец переходим к матрице D, высчитывая разность между столбцами (их становится на один меньше). Пользуясь этими значениями (предварительно посчитав сумму по столбцам), и количеством получившихся стимулов вычисляем из полученных различий шкальные значения стимулов, приняв, что S1 = 0, следующим образом:
Сведения об испытуемых: Студенты академической группы 17 человек.
Дата и время: 9.02.13. около 11.00
Результаты и их обработка
В результате прохождения теста мы получили автоматический протокол:
Время работы общее: 1 м. 39 с.
Продолжительность чистая: 1 м. 39 с.
Экспериментальный план: теплота_цвета
Тип эксперимента: Предпочтение
Стимулы предъявлялись одновременно
Сравнение внутри одной группы
Количество сессий: 5
Стимулы по порядку:
1: 2.bmp 2: 3.bmp 3: 5.bmp 4: 6.bmp 5: 1.bmp
Статистика по результатам тестирования:
Stimul X=1 X=2 X=3 X=4 X=5
Y=1 0 5 3 3 4
Y=2 0 0 0 0 1
Y=3 2 5 0 2 5
Y=4 2 5 3 0 5
Y=5 1 4 0 0 0
Цифры в матрице означают, сколько раз элемент X (отсчитываются по
горизонтали) был предпочтен элементу Y (отсчитываются по вертикали)
Общая сумма предпочтений для каждой пары, очевидно, равна 5
Ответы "равно" не допускались
Привожу свои данные (м1) и данные матрицы партнера (м2)по заданию Алиева Исмаила:
м1 м2
| № | 1 | 2 | 3 | 4 | 5 |
| 1 | 5 | 3 | 3 | 4 | |
| 2 | 0 | 0 | 0 | 1 | |
| 3 | 2 | 5 | 2 | 5 | |
| 4 | 2 | 5 | 3 | 5 | |
| 5 | 1 | 4 | 0 | 0 |
| № | 1 | 2 | 3 | 4 | 5 |
| 1 | 2 | 0 | 0 | 0 | |
| 2 | 3 | 0 | 1 | 0 | |
| 3 | 5 | 5 | 5 | 3 | |
| 4 | 5 | 4 | 0 | 0 | |
| 5 | 5 | 5 | 2 | 5 |
Усредненная матрица частот F:
| № | 1 | 2 | 3 | 4 | 5 |
| 1 | 3,5 | 1,5 | 1,5 | 2 | |
| 2 | 1,5 | 0 | 0,5 | 0,5 | |
| 3 | 3,5 | 5 | 3,5 | 4 | |
| 4 | 3,5 | 4,5 | 1,5 | 2,5 | |
| 5 | 3 | 4,5 | 1 | 2,5 |
Матрица вероятностей Р:
| № | 1 | 2 | 3 | 4 | 5 |
| 1 | 0.5 | 0,7 | 0,3 | 0,3 | 0,4 |
| 2 | 0,3 | 0.5 | 0 | 0,1 | 0,1 |
| 3 | 0,7 | 1 | 0.5 | 0,7 | 0,8 |
| 4 | 0,7 | 0,9 | 0,3 | 0.5 | 0,5 |
| 5 | 0,6 | 0,9 | 0,2 | 0,5 | 0.5 |
n = 5 (число предъявлений)
Матрица различий Z:
| № | 1 | 2 | 3 | 4 | 5 | |
| 1 | 0 | 0,52 | -0,52 | -0,52 | -0,25 | |
| 2 | -0,52 | 0 | - | -1,28 | -1,28 | |
| 3 | 0,52 | - | 0 | 0,52 | 0,84 | |
| 4 | 0,52 | 1,28 | -0,52 | 0 | 0 | |
| 5 | 0,25 | 1,28 | -0,84 | 0 | 0 | |
| сумма | 0,77 | 3,08 | -1,88 | -1,28 | -0,69 | |
Для вероятностей равных 0 или 1 z не существует.
Матрица различий Z`:
| № | 3 | 4 | 5 | 1 | 2 | ||||
| 1 | -0,52 | -0,52 | -0,25 | 0 | 0,52 | ||||
| 2 | - | -1,28 | -1,28 | -0,52 | 0 | ||||
| 3 | 0 | 0,52 | 0,84 | 0,52 | - | ||||
| 4 | -0,52 | 0 | 0 | 0,52 | 1,28 | ||||
| 5 | -0,84 | 0 | 0 | 0,25 | 1,28 | ||||
| сумма | -1,88 | -1,28 | -0,69 | 0,77 | 3,08 | ||||
Матрица разностей между столбцами D:
| № | d43 | d54 | d15 | d21 | |
| 1 | 0 | 0,27 | 0,25 | -0,52 | |
| 2 | - | 0 | 0,76 | 0,52 | |
| 3 | 0,52 | 0,32 | -0,32 | - | |
| 4 | 0,52 | 0 | -0,52 | 0,76 | |
| 5 | 0,84 | 0 | -0,52 | 1,03 | |
| сумма | 1,88 | 0,59 | -0,35 | 1,79 | |
| Число элементов | 4 | 5 | 5 | 4 | |
| значения | 0,47 | 0,12 | -0,07 | 0,45 | |
Вычисляем из полученных различий шкальные значения стимулов, приняв, что S2 = 0:
S2 = 0
S3 = 0 + 0,47 = 0,47
S4 = 0,47 + 0,12 = 0,59
S5 = 0,59 - 0,07 = 0,52
S1 =0,52+0,45 = 0,97
Недостающие элементы матрицы компенсируются наличием внутренней связи между элементами столбца, что позволяет рассматривать разность между столбцами матрицы как результат алгебраической интерполяции отсутствующих элементов в столбце.
Матрицы просчитаны двумя людьми, что повышает вероятность верности расчетов.
Обсуждение результатов
На основание полученных результатов располагаем стимулы теплоты цвета в континууме: 0; 0,47; 0,52; 0,59; 0,97 то есть у нас получается следующий порядок S2; S3; S5; S4; S1. Собственно это и является нашей интервальной шкалой.
К сожалению, у нас было всего 5 предъявлений вместо положенных 50 (по Гусеву), что с другой стороны значительно сократило выполнение задания и сэкономило время занятия.
Обсуждений результатов мало из-за отсутствия гипотезы, но в целом задание получилось объемным и интересным.
Даже после построения интервальной она мало что говорит, наверное стоит прилагать к материалам цветовые образцы, было бы интересно посмотреть почему стимул номер один стоит от стимула 2 на таком большом расстояние, и если матрицы рассчитаны верно то любопытно все же к каким цветам принадлежат кодовые значения S1…S5
Выводы
1. Освоение метод парных сравнений.
2. Построена интервальной шкалы.
Литература
1. Гусев А. Н., Измайлов Ч.А., Михалевская М.Б. Измерение в психологии: общий психологический практикум.