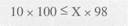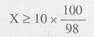ÚROK A MÍRA ČASOVÉ PREFERENCE
Úrok je nájemní cenou zapůjčitelných fondů. Platí jej ti, kdo chtějí investovat, těm, kdo spoří. Jak velký úrok požaduje ten, kdo spoří? Jak velký úrok musí dostat, aby odkládal svou spotřebu? A musí vůbec dostat nějaký úrok? Lidé přece spoří na horší časy - cožpak nebudou spořit i při nulovém úroku?
Úrok a míra časové preference
Spoření znamená odložení dnešní spotřeby do budoucna, či jinak řečeno, zřeknutí se dnešních statků ve prospěch budoucích statků. Představte si, že byste vyhráli nové auto a že byste dostali na vybranou: dostat jej dnes nebo až za rok. Jistě byste řekli, že jej chcete dnes. Ale proč vám není lhostejné, dostanete-li jej už dnes nebo až za rok? Protože jste netrpěliví— nemůžete se dočkat, až s ním budete jezdit. Skutečně, většina lidí má tuto vlastnost - netrpělivost ve spotřebě. Tím lze vysvětlit, proč preferují dnešní statky před budoucími statky. Této preferenci dnešních statků před budoucími statky říkáme též časová preference. Existence časové preference je příčinou toho, že lidé musí dostávat úrok, mají-li odkládat spotřebu do budoucna.
Autorem této teorie kapitálu a úroku byl Rakušan Eugen Bohm-Bawerk (Pozitivní teorie kapitálu, 1889). Dále ji rozpracoval Američan Irwing Fisher (Teorie úroku, 1930), který též zavedl pojem časová preference.
Ukažme si nejprve na jednoduchém příkladu vztah mezi úrokem a časovou preferencí.
Půjčka obilí
Pan Svoboda měl dobrou sklizeň obilí. Jeho soused však měl sklizeň horší, a proto jej přišel požádat o půjčku deseti pytlů obilí, kterou slibuje vrátit za rok.
Pan Svoboda však preferuje dnešní obilí před budoucím obilím. Dnešní obilí pro něho představuje dnešní spotřebu - kdyby prodal 10 pytlů obilí na trhu, mohl by si koupit nový televizor, kdežto půjčí-li obilí sousedovi, bude si moci koupit televizor až za rok. Předpokládejme, že pan Svoboda dokáže ocenit užitky dnešního i budoucího obilí určitými čísly. Dnešní pytel obilí ocení číslem 100 a budoucí pytel obilí ocení číslem 98. Jinak řečeno, pro pana Svobodu je pytel obilí za rok o zhruba dvě procenta méně užitečný než dnešní pytel obilí. Toto jeho ocenění dnešního a budoucího obilí odráží jeho „časovou preferenci", která je založena na netrpělivosti spotřeby.
|
|
| Nechce-li být pan Svoboda půjčkou poškozen, musí být pro něho užitek budoucích X pytlů obilí, které mu soused za rok vrátí, větší nebo alespoň stejný jako užitek dnešních deseti pytlů obilí: |
|
|
Pan Svoboda nevymění větší užitek za menší - nedá dnešní obilí za stejné množství obilí budoucího. Bude chtít přinejmenším vyrovnat užitky dnešního a budoucího obilí - bude proto od souseda požadovat, aby mu za rok vrátil větší množství obilí, než jaké mu dnes půjčuje. O kolik větší? To nám ukazuje následující nerovnice, jejíž levá strana udává, jak pan Svoboda oceňuje dnešní obilí, a pravá strana udává, jak oceňuje budoucí obilí. X je počet budoucích pytlů obilí, které bude chtít pan Svoboda za rok vrátit:
Kapitál a úrok
Řešením nerovnice pan Svoboda dojde k závěru, že počet za rok vrácených pytlů musí být alespoň 10,2. Jinak odmítne půjčku poskytnout. Oněch 0,2 pytle obilí je úrok. Jinak řečeno, pan Svoboda je ochoten půjčit sousedovi obilí na roční úrokovou míru 2 %.
V našem příkladě je míra časové preference pana Svobody 1,02 a úroková míra, kterou požaduje, je 0,02 neboli 2 %.
Příklad nám ukazuje rozhodování člověka, který spoří a půjčuje. Jeho rozhodování začíná oceněním současných a budoucích statků a porovnáním těchto ocenění. Ocení-li současné statky číslem A a tytéž, ovšem budoucí, statky ocení číslem B, pak poměr A : B udává jeho míru časové preference. Obecně řečeno, míra časové preference udává, kolikrát oceňuje člověk dnešní statky více než statky budoucí.
Úroková míra je určena mírou časové preference:
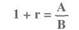
kde A/B je míra časové preference a r je úroková míra.
13.3