Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует.
Рассмотрим, например, такое неравенство
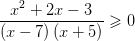
Метод интервалов позволяет решить его за пару минут.
В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.
Метод интервалов основан на следующем свойстве дробно-рациональной функции.
Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует.
Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. (Если вы не помните, что такое нули функции и знак функции на промежутке – смотрите статью «Исследование графика функции»).
Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида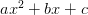 
.
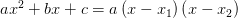, где 
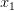и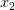 
— корни квадратного уравнения 
.
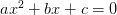Получим:
Рисуем ось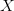 
и расставляем точки, в которых числитель и знаменатель обращаются в нуль.
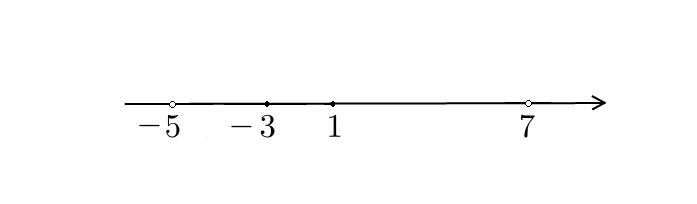
Нули знаменателя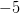 
и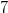 
- выколотые точки, так как в этих точках функция в левой части неравенства не определена (на нуль делить нельзя). Нули числителя 
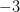и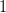 
- закрашены, так как неравенство нестрогое. Пр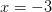и 
и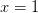 
наше неравенство выполняется, так как обе его части равны нулю.
Эти точки разбивают ось 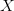на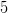 
промежутков.
Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным - либо "плюс", либо "минус".
И поэтому для определения знака функции на каждом таком промежутке мы берем любую точку, принадлежащую этому промежутку. Ту, которая нам удобна.
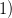
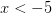. Возьмем, например, 
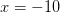и проверим знак выражения в левой части неравенства. Каждая из "скобок" отрицательная. Левая часть имеет знак 
.
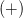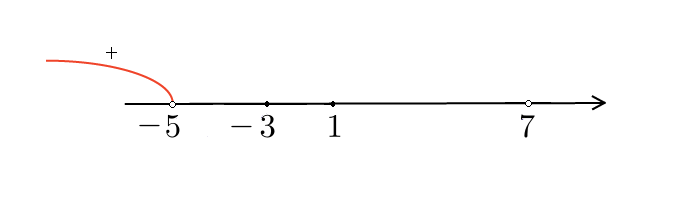
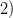Следующий промежуток: 
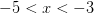. Проверим знак при 
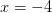. Получаем, что левая часть поменяла знак на 
.
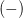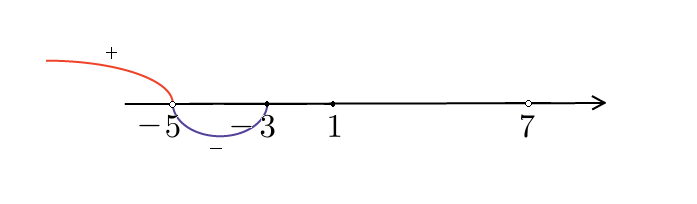
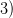
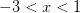. Возьмем 
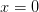. При 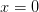выражение положительно - следовательно, оно положительно на всем промежутке от 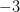до .
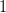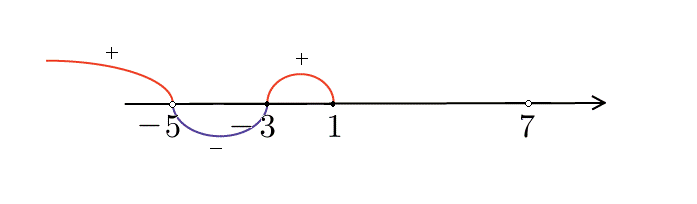
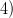При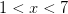 
левая часть неравенства отрицательна.
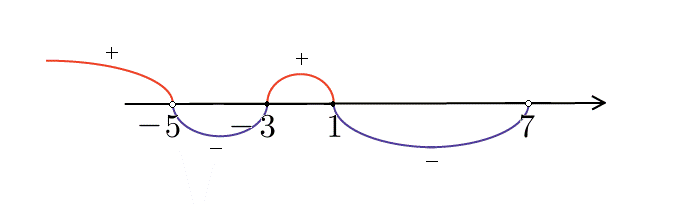
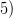И, наконец, 
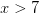. Подставим 
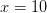и проверим знак выражения в левой части неравенства. Каждая "скобочка" положительна. Следовательно, левая часть имеет знак .
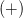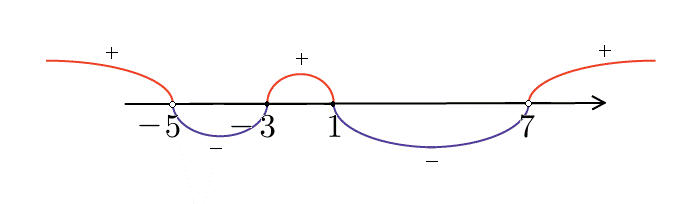
Мы нашли, на каких промежутках выражение положительно. Осталось записать ответ:
Ответ: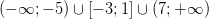 
.
Обратите внимание: знаки на промежутках чередуются. Это произошло потому, что при переходе через каждую точку ровно один из линейных множителей поменял знак, а остальные сохранили его неизменным.