Далее установим соотношение между и e. Барабан катится без скольжения по неподвижной плоскости, поэтому (см. рис. Д5), следовательно, точка B является мгновенным центром скоростей барабана. Тогда
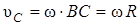 ,
, 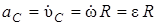 , или
, или
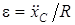 (5)
(5)
Подставляя кинематические уравнения (4), (5) в систему (1)-(3) и разделив уравнение (3) на R, получим
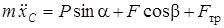 ; (6)
; (6)
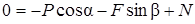 ; (7)
; (7)
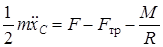 . (8)
. (8)
В уравнениях (6)-(8) остались три неизвестные 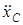 , N,
, N, 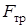 .
.
1) Определяем закона движения центра масс 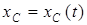 .
.
Сначала найдем 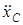 . Для этого сложим почленно равенства (6) и (8), тем самым исключив неизвестную
. Для этого сложим почленно равенства (6) и (8), тем самым исключив неизвестную 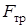 :
:
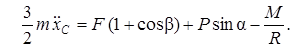
Подставляя численные значения, найдем
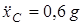 . (9)
. (9)
Интегрируя уравнение (9), получим
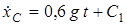 ; (10)
; (10)
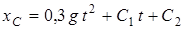 . (11)
. (11)
Начальные условия: 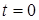 ,
, 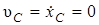 (так как движение начинается из состояния покоя),
(так как движение начинается из состояния покоя), 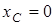 (так как ось y проходит через начальное положение точки
(так как ось y проходит через начальное положение точки 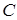 ). Подставляя эти начальные условия в (10) и (11), получим:
). Подставляя эти начальные условия в (10) и (11), получим: 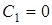 ,
, 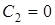 . Окончательно находим следующий закон движения центра масс
. Окончательно находим следующий закон движения центра масс 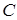 :
:
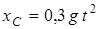 .
.
2) Определение минимального коэффициента трения 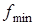 , при котором возможно качение барабана без скольжения.
, при котором возможно качение барабана без скольжения.
Сила трения должна удовлетворять условию
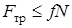 . (12)
. (12)
Найдем нормальную реакцию N из уравнения (7):
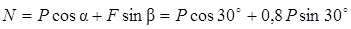 .
.
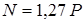 . (13)
. (13)
Значение 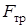 проще всего найти из уравнения (8), заменив в нем
проще всего найти из уравнения (8), заменив в нем 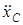 его значением (9). Получим
его значением (9). Получим
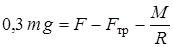 .
.
Отсюда
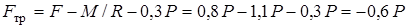 . (14)
. (14)
Знак указывает, что направление силы 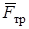 противоположно показанному на рисунке. Подставляя модуль значения
противоположно показанному на рисунке. Подставляя модуль значения 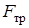 из (14) и значение
из (14) и значение 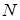 из (13) в неравенство (12), получим
из (13) в неравенство (12), получим
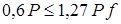 ,
,
откуда находим, что
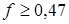 .
.
Следовательно, наименьший коэффициент трения, при котором возможно качение барабана без скольжения, равен 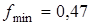 .
.
Ответ : 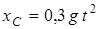 ,
, 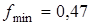 .
.
Задача Д 6
(тема: “ Принцип Даламбера для механической системы ”)
Вертикальный вал  (рис. Д6.0-Д6.9, табл. Д6), вращается с постоянной угловой скоростью
(рис. Д6.0-Д6.9, табл. Д6), вращается с постоянной угловой скоростью 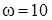 с-1. Вал имеет две опоры: подпятник в точке А и цилиндрический подшипник в точке, указанной в табл. Д6 (
с-1. Вал имеет две опоры: подпятник в точке А и цилиндрический подшипник в точке, указанной в табл. Д6 ( 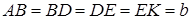 ). К валу жестко прикреплены невесомый стержень 1 длиной
). К валу жестко прикреплены невесомый стержень 1 длиной 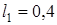 м с точечной массой
м с точечной массой 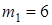 кг на конце и однородный стержень 2 длиной
кг на конце и однородный стержень 2 длиной 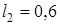 м, имеющий массу
м, имеющий массу 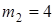 кг; оба стержня лежат в одной плоскости. Точки крепления стержней к валу и углы α и β указаны в таблице. Пренебрегая весом вала, определить реакции подпятника и подшипника. При окончательных подсчетах принять
кг; оба стержня лежат в одной плоскости. Точки крепления стержней к валу и углы α и β указаны в таблице. Пренебрегая весом вала, определить реакции подпятника и подшипника. При окончательных подсчетах принять 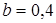 м.
м.
Перед выполнением задания прочтите по учебнику тему: «Принцип Даламбера». Ответьте на вопросы:
1. Сформулируйте принцип Даламбера для точки.
2. Как определяется модуль и направление силы инерции для точки? В каких случаях сила инерции равна нулю?
3. Сформулируйте принцип Даламбера для системы.
4. Чему равны главный вектор и главный момент сил инерции системы?
5. Запишите уравнения равновесия произвольной системы сил и плоской системы сил в координатной форме (вспомнив соответствующие уравнения статики).








