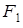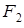Система приходит в движение из состояния покоя под действием силы , зависящей от перемещения s точки ее приложения. На шкив 3 при движении действует постоянный момент М сил сопротивления.
Дано: m1 = 8 кг, m2 = 0, m3 = 4 кг, m4 = 0, m5 = 10 кг, R3 = 0,3 м, r3 = 0,1 м, 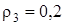 м, f = 0,1, с = 240 Н / м, М = 0,6 Н × м, F = 20 (3+2s) Н, s1 = 0,2м.
м, f = 0,1, с = 240 Н / м, М = 0,6 Н × м, F = 20 (3+2s) Н, s1 = 0,2м.
Определить: угловую скорость 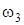 в тот момент времени, когда s = s1, где s1 – перемещение центра масс катка 1.
в тот момент времени, когда s = s1, где s1 – перемещение центра масс катка 1.
| 
| ||
| Рис. Д4 | |||
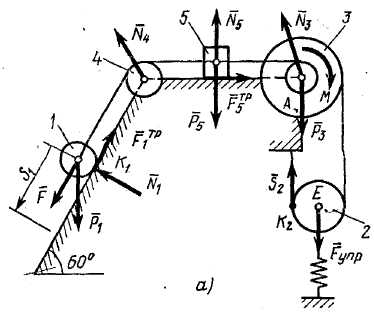
Решение. 1. Рассмотрим движение механической системы, состоящей из весомых тел 1, 3, 5 и невесомых тел 2, 4, соединенных нитями (рис. Д4а).
Для определения искомой угловой скорости 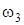 воспользуемся теоремой об изменении кинетической энергии системы в интегральной (конечной) форме:
воспользуемся теоремой об изменении кинетической энергии системы в интегральной (конечной) форме:
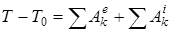 , (1)
, (1)
где 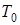 и
и 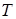 – кинетическая энергия системы в начальном и конечном положениях,
– кинетическая энергия системы в начальном и конечном положениях, 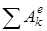 и
и 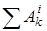 – алгебраические суммы работ действующих на систему внешних и внутренних сил при перемещении системы из начального положения в конечное.
– алгебраические суммы работ действующих на систему внешних и внутренних сил при перемещении системы из начального положения в конечное.
Сразу отметим в (1) равные нулю слагаемые. В начальный момент система находилась в покое, поэтому начальная кинетическая энергия равна нулю (Т0=0). Далее, так как система является неизменяемой, то 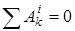 . Поэтому на рисунке изображены только внешние силы, действующие на тела системы, а внутренние силы не показаны.
. Поэтому на рисунке изображены только внешние силы, действующие на тела системы, а внутренние силы не показаны.
2. Определяем кинетическую энергию системы Т в конечном положении (левая часть уравнения (1)). Величина Т равна сумме кинетических энергий всех тел системы:
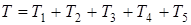 . (2)
. (2)
Так как по условию задачи массы тел 2 и 4 равны нулю, эти тела не обладают кинетической энергией, однако для общности изложения мы проведем здесь вычисление кинетической энергии этих тел (но при решении своей задачи следует сразу полагать кинетическую энергию тел, массами которых пренебрегаем, равной нулю).
Кинетическая энергия катка 1, совершающего плоское (сложное) движение, равна
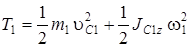 , (3)
, (3)
где 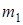 – масса катка 1,
– масса катка 1,
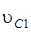 – скорость его центра масс
– скорость его центра масс 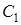 ,
,
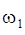 – угловая скорость катка 1,
– угловая скорость катка 1,
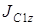 – момент инерции катка относительно оси, проходящей через его центр масс перпендикулярно плоскости катка. Так как каток 1 является однородным цилиндром, то
– момент инерции катка относительно оси, проходящей через его центр масс перпендикулярно плоскости катка. Так как каток 1 является однородным цилиндром, то
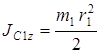 . (4)
. (4)
Кинетическая энергия блока 4, совершающего вращательное движение, равна
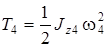 , (5)
, (5)
где 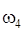 – угловая скорость блока 4,
– угловая скорость блока 4,
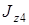 – момент инерции блока относительно оси, проходящей через его центр масс перпендикулярно плоскости блока. Если блок 4 является однородным диском, то
– момент инерции блока относительно оси, проходящей через его центр масс перпендикулярно плоскости блока. Если блок 4 является однородным диском, то 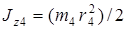 . Так как
. Так как 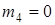 , то
, то 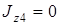 и, следовательно,
и, следовательно, 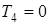 .
.
Кинетическая энергия груза 5, совершающего поступательное движение, равна
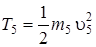 , (6)
, (6)
где 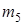 – масса груза 5,
– масса груза 5, 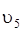 – его скорость.
– его скорость.
Кинетическая энергия блока 3, совершающего вращательное движение, равна
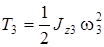 , (7)
, (7)
где 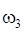 – угловая скорость блока 3,
– угловая скорость блока 3,
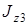 – момент инерции блока относительно оси, проходящей через его центр масс перпендикулярно плоскости блока. Так как блок 3 является ступенчатым, и для него заданы масса
– момент инерции блока относительно оси, проходящей через его центр масс перпендикулярно плоскости блока. Так как блок 3 является ступенчатым, и для него заданы масса 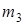 и радиус инерции
и радиус инерции 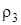 , то его момент инерции
, то его момент инерции 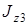 вычисляется по формуле:
вычисляется по формуле:
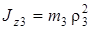 . (8)
. (8)
Кинетическая энергия подвижного блока 2, совершающего плоское (сложное) движение, равна
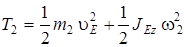 , (9)
, (9)
где 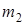 – масса подвижного блока 2,
– масса подвижного блока 2,
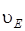 – скорость его центра масс
– скорость его центра масс 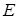 ,
,
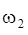 – угловая скорость подвижного блока 2,
– угловая скорость подвижного блока 2,
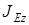 – момент инерции блока относительно оси, проходящей через его центр масс Е перпендикулярно плоскости блока. Если блок 2 является однородным диском, то
– момент инерции блока относительно оси, проходящей через его центр масс Е перпендикулярно плоскости блока. Если блок 2 является однородным диском, то 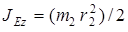 . Так как
. Так как 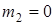 , то
, то 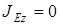 и, следовательно,
и, следовательно, 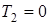 .
.
Таким образом, с учетом выражений (3)-(9) кинетическую энергию системы можно записать в виде:
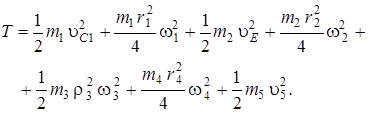 (10)
(10)
3. Выполняем кинематический расчет системы, т.е. выражаем все входящие в (10) линейные и угловые скорости ( 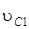 ,
, 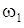 ,
, 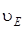 ,
, 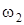 ,
, 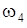 ,
, 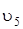 ) через искомую угловую скорость
) через искомую угловую скорость 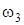 .
.
Каток 1 катится без скольжения по наклонной неподвижной плоскости, следовательно, абсолютная скорость точки K1 касания катка с плоскостью равна нулю. Поэтому точка K1 является мгновенным центром скоростей катка 1, откуда следует:
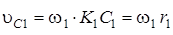 . (11)
. (11)
Первая нить, перекинутая через блок 4, соединяет центр катка С1 с грузом 5. Принимая во внимание, что нить нерастяжима и не скользит по блоку 4, получим
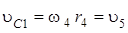 . (12)
. (12)
Вторая нить одним концом привязана к грузу 5, а другой ее конец намотан на малый барабан радиуса 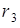 ступенчатого блока 3, поэтому
ступенчатого блока 3, поэтому
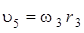 . (13)
. (13)
Из сравнения выражений (11)-(13) получаем:
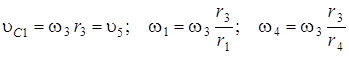 . (14)
. (14)
Третья нить одним концом привязана к неподвижной точке 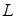 , а другой ее конец, огибая подвижный блок 2, намотан на большой барабан радиуса
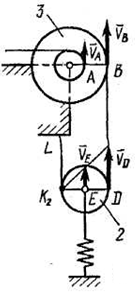
, а другой ее конец, огибая подвижный блок 2, намотан на большой барабан радиуса 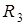 ступенчатого блока 3 (см. рис. Д4б). Участок нити
ступенчатого блока 3 (см. рис. Д4б). Участок нити 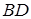 не скользит по блокам 2 и 3, поэтому
не скользит по блокам 2 и 3, поэтому
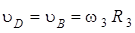 . (15)
. (15)
Подвижный блок 2 совершает плоское движение. Точка 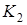 , в которой с блока 2 сходит неподвижный участок нити
, в которой с блока 2 сходит неподвижный участок нити 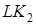 , является мгновенным центром скоростей для блока 2 (он как бы катится по участку нити
, является мгновенным центром скоростей для блока 2 (он как бы катится по участку нити 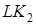 ). Отсюда следует:
). Отсюда следует:
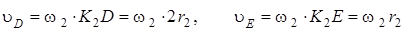 . (16)
. (16)
Из сравнения выражений (15) и (16) получаем:
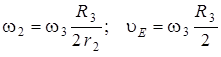 . (17)
. (17)
Подставив результаты кинематического расчета (14) и (17) в выражение для кинетической энергии (10), с учетом невесомости блоков 2 и 4 получаем окончательно:
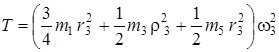 . (18)
. (18)
4. Вычисление работ сил. Укажем на рисунке все внешние силы (активные и реакции связей), действующие на точки системы (последовательно по рисунку рассматривая тела системы, начиная с катка 1): 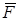 ,
, 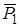 ,
, 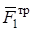 ,
, 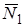 ,
, 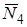 ,
, 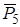 ,
, 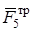 ,
, 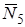 ,
, 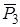 , М,
, М, 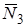 ,
, 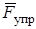 ,
, 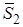 . Здесь учтено, что
. Здесь учтено, что 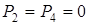 . Теперь найдем сумму работ всех действующих внешних сил при том перемещении, которое будет иметь система, когда центр С1 катка 1 пройдет путь s1.
. Теперь найдем сумму работ всех действующих внешних сил при том перемещении, которое будет иметь система, когда центр С1 катка 1 пройдет путь s1.
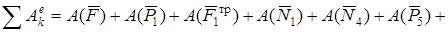
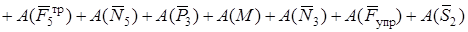 .
.
Отметим в этом выражении равные нулю слагаемые (последовательно по рисунку рассматривая тела системы, начиная с катка 1).
Каток 1 .
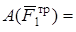
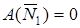 , так как скорость точки
, так как скорость точки 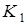 приложения этих сил равна нулю (качение без скольжения). Следует отметить, что модуль силы трения
приложения этих сил равна нулю (качение без скольжения). Следует отметить, что модуль силы трения 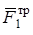 не равен произведению коэффициента трения на нормальную реакцию. При качении без скольжения сила трения должна лишь удовлетворять неравенству
не равен произведению коэффициента трения на нормальную реакцию. При качении без скольжения сила трения должна лишь удовлетворять неравенству 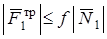 (определение силы трения при качении рассмотрено в задаче Д5). Работы
(определение силы трения при качении рассмотрено в задаче Д5). Работы 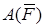 и
и 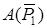 будут вычислены ниже.
будут вычислены ниже.
Блок 4 .
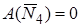 , так как реакция
, так как реакция 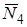 приложена к точке, лежащей на неподвижной оси блока 4.
приложена к точке, лежащей на неподвижной оси блока 4.
Груз 5 .
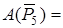
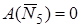 , так как силы перпендикулярны скоростям точек, в которых они приложены. Работа
, так как силы перпендикулярны скоростям точек, в которых они приложены. Работа 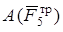 будет вычислена ниже.
будет вычислена ниже.
Шкив 3 .
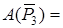
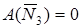 , так как силы приложены к точке, лежащей на неподвижной оси блока 3. Работа
, так как силы приложены к точке, лежащей на неподвижной оси блока 3. Работа 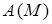 будет вычислена ниже.
будет вычислена ниже.
Подвижный блок 2 .
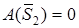 , так как скорость точки
, так как скорость точки 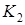 приложения реакция
приложения реакция 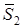 равна нулю (блок 2 катится без скольжения по неподвижной части нити, подобно тому, как каток 1 катится по неподвижной плоскости). Работа
равна нулю (блок 2 катится без скольжения по неподвижной части нити, подобно тому, как каток 1 катится по неподвижной плоскости). Работа 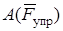 будет вычислена ниже.
будет вычислена ниже.
Таким образом, сумма работ всех действующих внешних сил
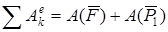
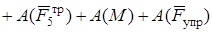 .
.
Вычислим каждое из этих слагаемых (последовательно по рисунку рассматривая тела системы, начиная с катка 1).
Каток 1.
Вычислим 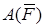 . Так как сила
. Так как сила 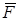 зависит от переменной s, то работа силы
зависит от переменной s, то работа силы 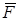 на конечном перемещении определяется выражением:
на конечном перемещении определяется выражением:
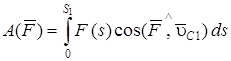 .
.
Сила 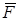 совпадает по направлению со скоростью
совпадает по направлению со скоростью 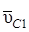 центра катка 1,
центра катка 1, 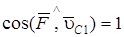 , тогда
, тогда
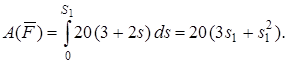 (19)
(19)
Вычислим 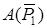 . Сила тяжести
. Сила тяжести 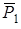 постоянна и образует со скоростью
постоянна и образует со скоростью 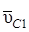 угол
угол 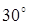 . Работа силы
. Работа силы 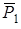 :
:
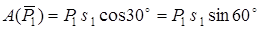 (20)
(20)
Груз 5 .
Вычислим работу 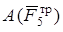 . Сначала найдем величину
. Сначала найдем величину 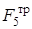 силы трения. Она определяется аналогично тому, как это было сделано в задаче Д1. Выделим из системы груз 5. На него действуют силы:
силы трения. Она определяется аналогично тому, как это было сделано в задаче Д1. Выделим из системы груз 5. На него действуют силы: 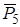 ,
, 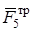 ,
, 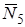 ,
, 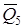 , где
, где 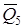 – суммарная реакция левой и правой частей нити. Уравнение движения груза 5 имеет вид:
– суммарная реакция левой и правой частей нити. Уравнение движения груза 5 имеет вид:
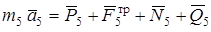 ,
,
где 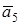 – ускорение груза 5, совпадающее по направлению с его скоростью
– ускорение груза 5, совпадающее по направлению с его скоростью 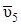 . Спроектируем это уравнение на ось у, перпендикулярную направлению движения груза 5 (см. рис. Д1 и пример решения задачи Д1):
. Спроектируем это уравнение на ось у, перпендикулярную направлению движения груза 5 (см. рис. Д1 и пример решения задачи Д1):
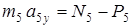 ,
,
Так как 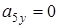 , то
, то 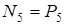 и
и 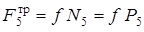 . В случае движения груза по наклонной плоскости следует ось y выбрать перпендикулярно плоскости движения груза. Сила трения
. В случае движения груза по наклонной плоскости следует ось y выбрать перпендикулярно плоскости движения груза. Сила трения 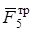 направлена противоположно скорости груза
направлена противоположно скорости груза 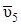 ,
, 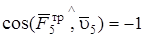 , поэтому работа силы трения отрицательна:
, поэтому работа силы трения отрицательна:
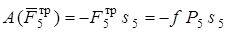 . (21)
. (21)
Шкив 3.
Вычислим работу 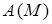 . Момент сопротивления М направлен противоположно направлению вращения блока, поэтому его работа отрицательна:
. Момент сопротивления М направлен противоположно направлению вращения блока, поэтому его работа отрицательна:
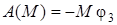 . (22)
. (22)
Подвижный блок 2 .
Вычислим работу 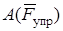 . Работа силы упругости пружины
. Работа силы упругости пружины 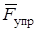 равна:
равна:
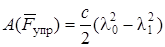 ,
,
где с – жесткость пружины, 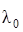 и
и 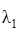 – начальное и конечное удлинения пружины.
– начальное и конечное удлинения пружины.
По условию задачи начальная деформация пружины отсутствует, 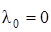 . Конечное удлинение пружины равно перемещению
. Конечное удлинение пружины равно перемещению 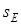 конца пружины
конца пружины 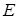 , совпадающего с центром блока 2, тогда:
, совпадающего с центром блока 2, тогда:
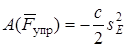 , (23)
, (23)
Таким образом, сумма работ внешних сил, действующих на точки системы, равна:
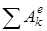
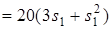
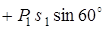
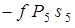
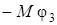
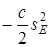 (24)
(24)
5. Так как зависимость между линейными и угловыми перемещениями такая же, как между соответствующими скоростями, с помощью результатов кинематического расчета (14) и (17) выразим входящие в выражение (24) перемещения 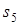 ,
, 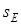 и угол поворота
и угол поворота 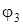 через перемещение s1:
через перемещение s1:
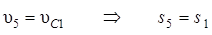 ;
;
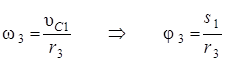 ;
;
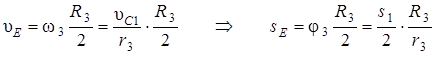 .
.
Подставляя эти соотношения в (24), выразим сумму работ внешних сил через заданное перемещение s1 тела 1:
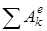
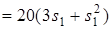
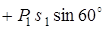
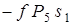
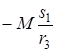
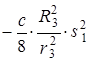 . (25)
. (25)
5. Подставив выражения кинетической энергии (18) и и суммы работ внешних сил (25) в уравнение (1) и учитывая, что T0 = 0 и 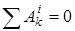 , приходим к равенству:
, приходим к равенству:
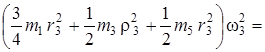
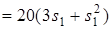
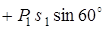
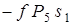
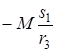
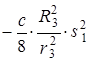 .
. 
Подставляя в это равенство числовые значения, которые имеют заданные величины, находим искомую угловую скорость 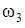 .
.
Ответ: 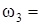 8,1 с -1.
8,1 с -1.
Задача Д 5
(тема: “Динамика плоскопараллельного движения твердого тела ”)
Барабан радиуса 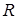 весом
весом 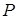 имеет выточку (как у катушки) радиуса
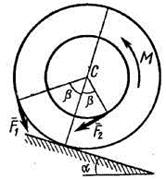
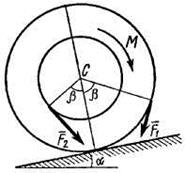
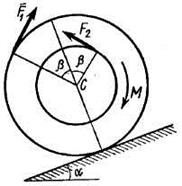
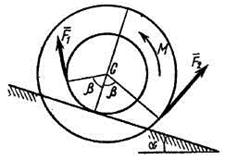
имеет выточку (как у катушки) радиуса 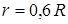 (рис. Д5.0-Д5.9, табл. Д5). К концам намотанных на барабан нитей приложены постоянные силы
(рис. Д5.0-Д5.9, табл. Д5). К концам намотанных на барабан нитей приложены постоянные силы 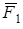 и
и 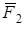 , направления которых определяются углом
, направления которых определяются углом 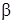 ; кроме сил на барабан действует пара с моментом
; кроме сил на барабан действует пара с моментом 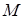 ; когда в таблице
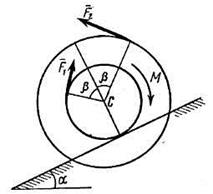
; когда в таблице 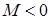 , направление момента противоположно показанному на рисунке. При движении, начинающемся из состояния покоя, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона α так, как показано на рисунках.
, направление момента противоположно показанному на рисунке. При движении, начинающемся из состояния покоя, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона α так, как показано на рисунках.
Пренебрегая сопротивлением качению, определить закон движения центра масс 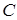 барабана, т.е.
барабана, т.е. 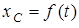 , и наименьшее значение коэффициента трения
, и наименьшее значение коэффициента трения 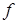 о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса
о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса 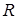 .
.
Перед выполнением задания прочтите по учебнику тему: «Дифференциальные уравнения плоского движения твердого тела».
Ответьте на вопросы:
1. Запишите дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси.
2. В каком случае дифференциальное уравнение вращательного движения вокруг подвижной оси имеет тот же вид, что и уравнение вращательного движения относительно неподвижной оси?
3. На какие простые движения и как раскладывается плоскопараллельное движение тела (кинематика)?
4. Запишите дифференциальные уравнения плоскопараллельного движения твердого тела.
5. Какое соотношение связывает угловую скорость катящегося тела и скорость его центра масс при качении без скольжения?
6. В каких пределах может изменяться сила трения при качении тела?
| 
|
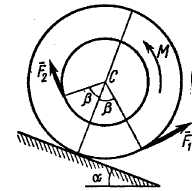
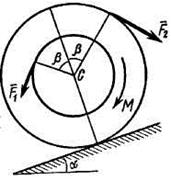
| Рис. Д5.0 | Рис. Д5.1 |
| 
|
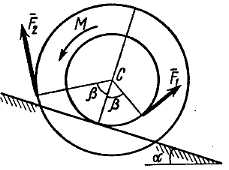
| Рис. Д5.2 | Рис. Д5.3 |
| 
|
| Рис. Д5.4 | Рис. Д5.5 |
| 
|
| Рис. Д5.6 | Рис. Д5.7 |
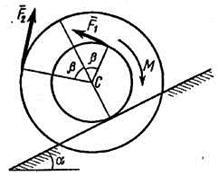
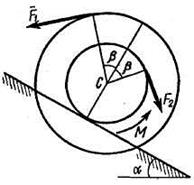
| 
|
| Рис. Д5.8 | Рис. Д5.9 |
Таблица Д5
| Номер условия | α | 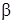
|
|
|
|
| град | |||||
| 0 | 30 | 60 | 0 | 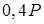
| 0 |
| 1 | 30 | 30 | 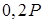
| 0 | 0 |
| 2 | 0 | 30 | 0 | 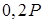
| 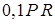
|
| 3 | 30 | – | 0 | 0 | 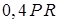
|
| 4 | 30 | 90 | 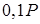
| 0 | 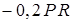
|
| 5 | 0 | 60 | 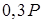
| 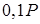
| 0 |
| 6 | 30 | 0 | 0 | 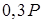
| 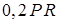
|
| 7 | 0 | 60 | 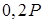
| 0 | 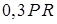
|
| 8 | 30 | 90 | 0 | 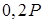
| 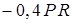
|
| 9 | 30 | 60 | 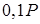
| 0 | 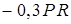
|
Динамика плоскопараллельного движения твердого тела
(краткие сведения из теории)
Плоскопараллельное движение твердого тела – это составное движение. Выбирая за полюс центр масс C тела, раскладываем плоскопараллельное движение на переносное поступательное, при котором все точки движутся как полюс C, и относительное вращательное вокруг оси Cz, проходящей через C перпендикулярно плоскости сечения тела.
Дифференциальные уравнения плоскопараллельного движения твердого тела представляют собой систему уравнений: уравнение (1) движения центра масс и уравнение (2) вращательного движения твердого тела вокруг оси Cz, проходящей через центр масс тела и движущейся поступательно вместе с центром масс. Поэтому второе уравнение совпадает с уравнением вращательного движения тела вокруг неподвижной оси.
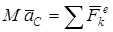 , (1) , (1)
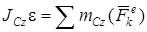 . (2)
Проектируя векторное уравнение (1) на взаимно перпендикулярные оси x и y, параллельные плоскости сечения тела, получим уравнения движения тела в координатной (алгебраической форме): . (2)
Проектируя векторное уравнение (1) на взаимно перпендикулярные оси x и y, параллельные плоскости сечения тела, получим уравнения движения тела в координатной (алгебраической форме):
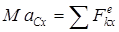 , ,
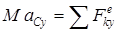 , ,
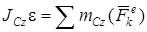 .
Эти уравнения обычно дополняются кинематическими уравнениями, дающими, в частности, соотношение между угловым ускорением e тела и ускорением .
Эти уравнения обычно дополняются кинематическими уравнениями, дающими, в частности, соотношение между угловым ускорением e тела и ускорением 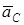 центра масс тела. Решая эту полученную систему динамических и кинематических уравнений, можно находить как ускорения, так и силы, в зависимости от условий и вопросов задачи (первая и вторая задачи динамики). центра масс тела. Решая эту полученную систему динамических и кинематических уравнений, можно находить как ускорения, так и силы, в зависимости от условий и вопросов задачи (первая и вторая задачи динамики).
|
Указания. Задача Д5 – на применение дифференциальных уравнений плоскопараллельного движения твердого тела. При составлении уравнений следует, во избежание ошибок в знаках, направить координатную ось x в ту сторону, куда предполагается направленным движение центра 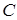 барабана, и считать тогда все моменты положительными, когда они направлены в сторону вращения барабана. Если фактически направление движения центра другое, то в ответе получится
барабана, и считать тогда все моменты положительными, когда они направлены в сторону вращения барабана. Если фактически направление движения центра другое, то в ответе получится 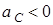 , но найденное значение
, но найденное значение 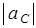 будет верным. Силу трения, когда неясно, куда она направлена, можно направлять в любую сторону (результат от этого не зависит).
будет верным. Силу трения, когда неясно, куда она направлена, можно направлять в любую сторону (результат от этого не зависит).
Составленные динамические уравнения следует дополнить кинематическими, дающими, в частности, соотношение между 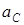 и угловым ускорением e тела.
и угловым ускорением e тела.
Определяя наименьшее значения коэффициента трения, при котором возможно качение без скольжения, учесть, что сила трения не может быть больше предельной, т.е. что 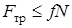 , откуда
, откуда 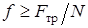 . Следовательно,
. Следовательно, 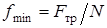 . Если при расчетах получится
. Если при расчетах получится 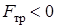 , то это означает, что сила
, то это означает, что сила 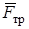 направлена в другую сторону и
направлена в другую сторону и 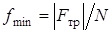 ; в остальном весь расчет будет верен (N в данной задаче не может получиться <0, так как барабан не отрывается от поверхности).
; в остальном весь расчет будет верен (N в данной задаче не может получиться <0, так как барабан не отрывается от поверхности).
Пример Д5. Барабан (сплошной однородный цилиндр) радиуса 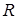 и весом
и весом 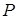 начинает катиться без скольжения из состояния покоя по наклонной плоскости с углом наклона α, на барабан действуют сила
начинает катиться без скольжения из состояния покоя по наклонной плоскости с углом наклона α, на барабан действуют сила 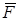 , направление которой определяется углом
, направление которой определяется углом 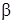 , и пара сил с моментом
, и пара сил с моментом 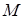 (рис. Д5).
(рис. Д5).
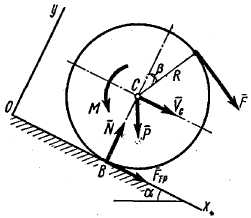 Рис . Д5
Рис . Д5
| Дано: 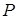 , , 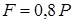 , , 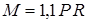 , ,
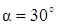 , , 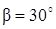 .
Определить:
1) .
Определить:
1) 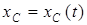 – закон движения центра масс барабана;
2) – закон движения центра масс барабана;
2) 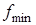 – наименьший коэффициент трения, при котором возможно качение без скольжения. – наименьший коэффициент трения, при котором возможно качение без скольжения.
|
Решение. Барабан совершает плоскопараллельное движение под действием сил 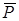 ,
, 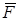 ,
, 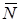 ,
, 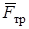 и пары сил, момент которой равен
и пары сил, момент которой равен 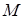 . Так как направление силы трения
. Так как направление силы трения 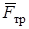 заранее неизвестно, выбираем его произвольно. Ось x проводим вдоль наклонной плоскости вниз, ось
заранее неизвестно, выбираем его произвольно. Ось x проводим вдоль наклонной плоскости вниз, ось 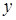 проводим перпендикулярно наклонной плоскости так, чтобы начальное положение центра масс находилось на оси y.
проводим перпендикулярно наклонной плоскости так, чтобы начальное положение центра масс находилось на оси y.
Составляем дифференциальные уравнения плоскопараллельного движения барабана:
– дифференциальное уравнение движения центра масс в векторной форме:
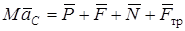 ;
;
– дифференциальные уравнения движения центра масс в проекциях на оси:
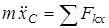 ;
; 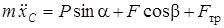 ; (1)
; (1)
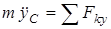 ;
; 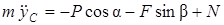 ; (2)
; (2)
– дифференциальное уравнение вращательного движения барабана относительно подвижной оси 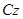 , проходящей через центр масс и движущейся поступательно вместе с центром масс барабана:
, проходящей через центр масс и движущейся поступательно вместе с центром масс барабана:
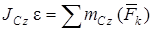 ;
; 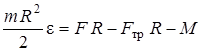 . (3)
. (3)
За положительное направление для моментов сил принято направление в ту сторону, куда будет вращаться барабан при движении центра от оси 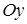 .
.
В систему уравнений (1)-(3) входят пять неизвестных: 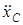 ,
, 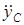 , e, N,
, e, N, 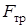 . Дополним эту систему двумя кинематическими уравнениями; для этого выполним кинематические расчеты. Так как в задаче
. Дополним эту систему двумя кинематическими уравнениями; для этого выполним кинематические расчеты. Так как в задаче 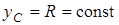 , то
, то
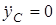 . (4)
. (4)