Подставив это значение в уравнение (9), определим искомую зависимость N от t.
Подставляя эти выражения в формулу (10) и учитывая заданные зависимости 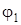 и
и 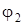 от t, получим
от t, получим
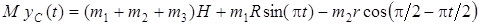
или 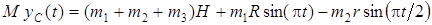 .
.
Продифференцировав обе части этого равенства два раза по времени, найдем 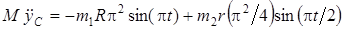 .
.
Подставив это значение 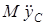 в уравнение (9), определим искомую зависимость N от t.
в уравнение (9), определим искомую зависимость N от t.
Ответ : 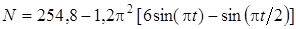 , где t – в секундах, N – в ньютонах.
, где t – в секундах, N – в ньютонах.
Задача Д3
(тема : “Теорема об изменении кинетического момента
системы относительно оси ”)
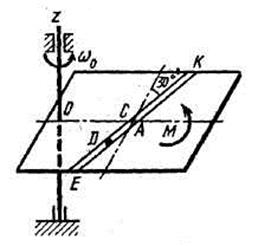
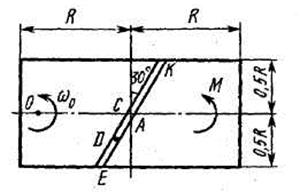
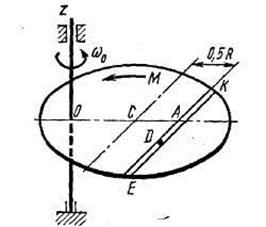
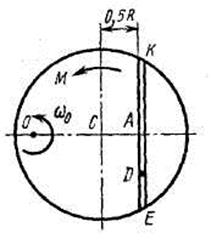
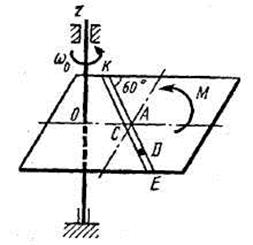
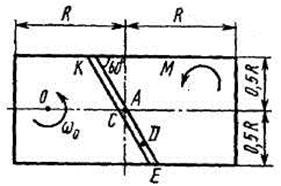
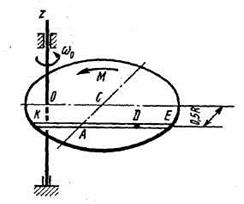
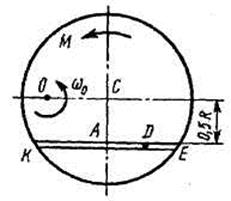
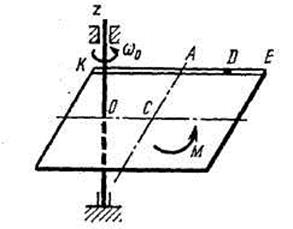
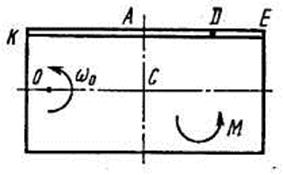
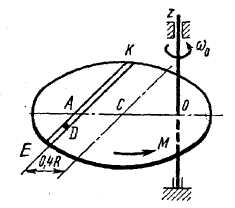
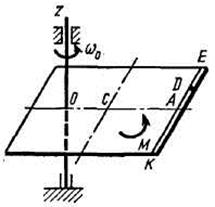
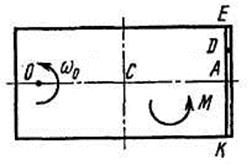
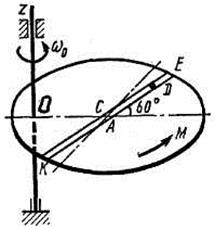
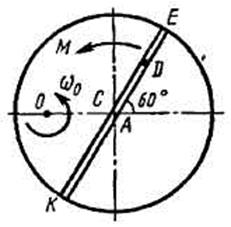
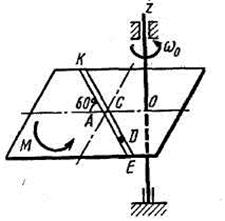
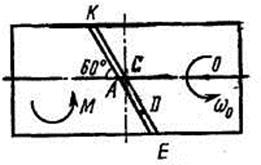
Однородная горизонтальная платформа (круглая радиуса 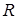 или прямоугольная со сторонами
или прямоугольная со сторонами 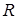 и
и 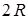 , где R=1,2 м) массой
, где R=1,2 м) массой 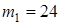 кг вращается с угловой скоростью
кг вращается с угловой скоростью 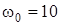 с-1 вокруг вертикальной оси
с-1 вокруг вертикальной оси 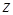 , отстоящей от центра масс
, отстоящей от центра масс 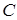 платформы на расстояние
платформы на расстояние 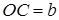 (рис. Д3.0-Д3.9, табл. Д3); размеры для всех прямоугольных платформ показаны на рис. Д3.0а (вид сверху).
(рис. Д3.0-Д3.9, табл. Д3); размеры для всех прямоугольных платформ показаны на рис. Д3.0а (вид сверху).
В момент времени 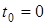 по желобу платформы начинает двигаться (под действием внутренних сил) груз
по желобу платформы начинает двигаться (под действием внутренних сил) груз 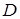 массой
массой 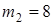 кг по закону
кг по закону 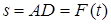 , где s выражено в метрах, а
, где s выражено в метрах, а 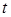 – в секундах. Одновременно на платформу начинает действовать пара сил с моментом
– в секундах. Одновременно на платформу начинает действовать пара сил с моментом 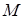 (задан в Ньютоно-метрах; при
(задан в Ньютоно-метрах; при 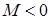 его направление противоположно показанному на рисунке).
его направление противоположно показанному на рисунке).
Определить, пренебрегая массой вала, зависимость 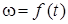 , т.е. угловую скорость платформы, как функцию времени.
, т.е. угловую скорость платформы, как функцию времени.
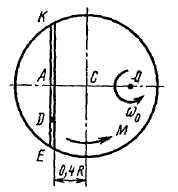
На всех рисунках груз D показан в положении, при котором 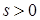 (когда
(когда 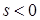 , груз находится по другую сторону от точки
, груз находится по другую сторону от точки  ). Изображая чертеж решаемой задачи, провести ось
). Изображая чертеж решаемой задачи, провести ось 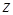 на заданном расстоянии
на заданном расстоянии 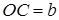 от центра
от центра 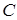 .
.
Перед выполнением задания прочтите по учебнику тему: «Теорема об изменении кинетического момента системы». Ответьте на вопросы:
1. Вычисление моментов количества движения материальной точки относительно неподвижного центра и неподвижной оси.
2. Определения: кинетический момент механической системы относительно неподвижного центра и неподвижной оси.
3. Сформулируйте теоремы об изменении кинетических моментов механической системы относительно неподвижного центра и неподвижной оси, запишите соответствующие уравнения.
4. Чему равен кинетический момент вращающегося твердого тела относительно оси вращения?
5. Что такое момент инерции твердого тела относительно оси? Что такое радиус инерции?
6. Сформулируйте теорему о моментах инерции относительно параллельных осей.
7. Запишите дифференциальное уравнение вращательного движения твердого тела относительно неподвижной оси.
Таблица Д3
| Номер условия | 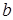 , м , м
| 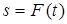 , м , м
| М, Нм |
| 0 | R | – 0,4 t 2 | 6 |
| 1 | R / 2 | – 0,6 t 2 | 4 t |
| 2 | R | – 0,8 t 2 | – 6 |
| 3 | R / 2 | 10 t | – 8 t |
| 4 | R | 0,4 t 3 | 10 |
| 5 | R / 2 | – 0,5 t | – 9 t 2 |
| 6 | R | – 0,6 t | 8 |
| 7 | R / 2 | 0,8 t | 6 t 2 |
| 8 | R | 0,4 t 3 | – 10 t |
| 9 | R / 2 | 0,5 t 2 | 12 t 2 |
| 
|
| Рис . Д3.0 | Рис . Д3.0а |
| 
|
| Рис . Д3.1 | Рис . Д3.1а |
| 
|
| Рис . Д3.2 | Рис . Д3.2а |
| 
|
| Рис . Д3.3 | Рис . Д3.3а |
| 
|
| Рис . Д3.4 | Рис . Д3.4а |
| 
|
| Рис . Д3.5 | Рис . Д3.5а |
| 
|
| Рис . Д3.6 | Рис . Д3.6а |
| 
|
| Рис . Д3.7 | Рис . Д3.7а |
| 
|
| Рис . Д3.8 | Рис . Д3.8а |
| 
|
| Рис . Д3.9 | Рис . Д3.9а |
Теорема об изменении кинетического момента механической системы
(краткие сведения из теории)
Основные понятия
Количество движения (импульс) точки – это вектор, равный 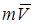 , где m –масса точки, , где m –масса точки, 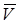 – абсолютная скорость точки.
Момент количества движения точки относительно какой-либо оси z – абсолютная скорость точки.
Момент количества движения точки относительно какой-либо оси z 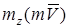 определяется так же, как момент силы относительно оси z определяется так же, как момент силы относительно оси z 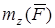 ; в частности, ; в частности, 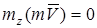 если вектор если вектор 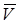 параллелен z или прямая, на которой расположен вектор параллелен z или прямая, на которой расположен вектор 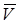 , пересекает ось z.
Кинетический момент системы , пересекает ось z.
Кинетический момент системы 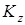 относительно какой-либо оси z равен (алгебраической) сумме моментов количеств движения точек относительно этой оси: относительно какой-либо оси z равен (алгебраической) сумме моментов количеств движения точек относительно этой оси:
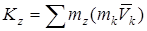 .
Кинетический момент вращающегося твердого тела относительно (неподвижной) оси вращения z равен .
Кинетический момент вращающегося твердого тела относительно (неподвижной) оси вращения z равен
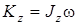 , (1)
где , (1)
где 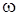 – угловая скорость тела, – угловая скорость тела,
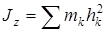 –
– момент инерции тела относительно оси z; здесь –
– момент инерции тела относительно оси z; здесь 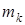 – масса точки тела, – масса точки тела, 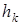 – расстояние от этой точки до оси z.
Момент инерции тела зависит от формы тела и положения оси z. Значения – расстояние от этой точки до оси z.
Момент инерции тела зависит от формы тела и положения оси z. Значения 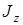 для однородных тел простой формы (кольцо, стержень, диск, прямоугольник, цилиндр и т. д.) приводятся в справочниках по механике; значения для однородных тел простой формы (кольцо, стержень, диск, прямоугольник, цилиндр и т. д.) приводятся в справочниках по механике; значения 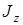 , необходимые для решения данной задачи, приведены ниже в указаниях к решению.
Если задан радиус инерции r тела, то , необходимые для решения данной задачи, приведены ниже в указаниях к решению.
Если задан радиус инерции r тела, то 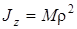 , где M – масса тела.
Теорема Гюйгенса (теорема о моментах инерции относительно параллельных осей): , где M – масса тела.
Теорема Гюйгенса (теорема о моментах инерции относительно параллельных осей): 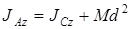 ; где ; где 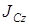 – момент инерции тела относительно оси, проходящей через центр масс, – момент инерции тела относительно оси, проходящей через центр масс, 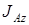 – момент инерции тела относительно оси Az, параллельной оси Cz, M – масса тела, d – расстояние между осями Az и Cz. – момент инерции тела относительно оси Az, параллельной оси Cz, M – масса тела, d – расстояние между осями Az и Cz.
|
Теорема об изменении кинетического момента системы относительно неподвижной оси
Формулировка: производная по времени от кинетического момента системы относительно неподвижной оси z равна (алгебраической) сумме моментов внешних сил относительно этой оси; математическая запись:
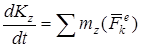 . (2)
Частный случай (закон сохранения . (2)
Частный случай (закон сохранения 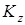 )
Если внешние силы таковы, что )
Если внешние силы таковы, что 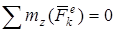 , то , то 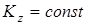 , то есть , то есть 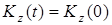 .
Дифференциальное уравнение вращательного движения твердого тела
Для вращающегося твердого тела, подставляя (1) в (2) и учитывая, что .
Дифференциальное уравнение вращательного движения твердого тела
Для вращающегося твердого тела, подставляя (1) в (2) и учитывая, что 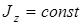 , найдем , найдем
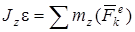 –
– дифференциальное уравнение вращательного движения твердого тела; здесь –
– дифференциальное уравнение вращательного движения твердого тела; здесь 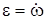 – угловое ускорение тела. – угловое ускорение тела.
|
Указания. Задача ДЗ – на применение теоремы об изменении кинетического момента системы. При применении теоремы к системе, состоящей из платформы и груза, кинетический момент  системы относительно оси
системы относительно оси 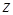 определяется как алгебраическая сумма кинетического момента платформы и момента количества движения груза. При этом следует учесть, что количество движения груза равно произведению его массы на абсолютную скорость
определяется как алгебраическая сумма кинетического момента платформы и момента количества движения груза. При этом следует учесть, что количество движения груза равно произведению его массы на абсолютную скорость 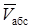 , которая складывается из относительной
, которая складывается из относительной 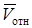 и переносной
и переносной 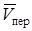 скоростей, т.е.
скоростей, т.е. 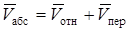 . Поэтому и количество движения этого груза
. Поэтому и количество движения этого груза 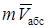 равно
равно 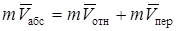 . Тогда для вычисле-ния момента количества движения груза
. Тогда для вычисле-ния момента количества движения груза 
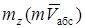 можно воспользоваться теоремой Вариньона (статика):
можно воспользоваться теоремой Вариньона (статика): 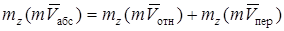 ; эти моменты вычисляются так же, как моменты сил. Подробнее ход решения разъяснен в примере Д3.
; эти моменты вычисляются так же, как моменты сил. Подробнее ход решения разъяснен в примере Д3.
При решении задачи полезно изобразить на вспомогательном чертеже вид платформы сверху (с конца оси  ), как это сделано на рис. Д3.0а-Д3.9а.
), как это сделано на рис. Д3.0а-Д3.9а.
Момент инерции однородной пластины массы m относительно оси  , перпендикулярной пластине и проходящей через ее центр масс
, перпендикулярной пластине и проходящей через ее центр масс 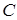 , равен:
, равен:
для прямоугольной пластины со сторонами 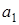 и и 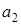
| 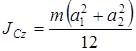 ; ;
|
для круглой пластины радиуса 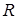
| 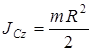 . .
|
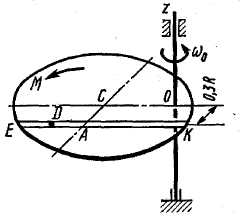
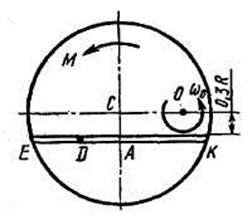
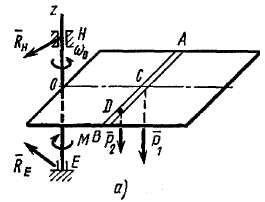
Пример ДЗ. Однородная горизонтальная платформа (прямоугольная со сторонами 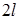 и
и 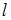 ), имеющая массу
), имеющая массу 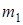 , жестко скреплена с вертикальным валом и вращается вместе с ним вокруг оси
, жестко скреплена с вертикальным валом и вращается вместе с ним вокруг оси 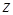 с угловой скоростью
с угловой скоростью 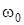 (рис. ДЗа). В момент времени
(рис. ДЗа). В момент времени 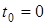 на вал начинает действовать пара сил с вращающим моментом
на вал начинает действовать пара сил с вращающим моментом 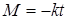 (на рис. Д3 отрицательный знак M уже учтен в показанных противоположных направлениях M и
(на рис. Д3 отрицательный знак M уже учтен в показанных противоположных направлениях M и 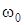 ); одновременно груз
); одновременно груз 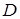 массой
массой 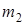 , находящийся в желобе
, находящийся в желобе 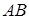 в точке
в точке 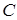 , начинает двигаться по желобу (под действием внутренних сил) по закону
, начинает двигаться по желобу (под действием внутренних сил) по закону 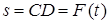 .
.
Дано: m1 = 16 кг, m2 = 10 кг, l = 0,5м, 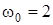 с-1,
с-1, 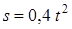 (s – в метрах,
(s – в метрах, 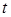 – в секундах),
– в секундах), 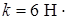 м/с.
м/с.
Определить: 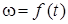 – закон изменения угловой скорости платформы.
– закон изменения угловой скорости платформы.
| 
|
| Рис. Д3 | |
Решение. Рассмотрим механическую систему, состоящую из платформы и груза  . Для определения угловой скорости
. Для определения угловой скорости  применим теорему об изменении кинетического момента системы относительно оси z:
применим теорему об изменении кинетического момента системы относительно оси z:
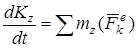 . (1)
. (1)
Изобразим действующие на систему внешние силы: силы тяжести 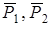 , реакции подпятника
, реакции подпятника 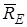 , подшипника
, подшипника 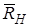 и вращающий момент
и вращающий момент 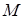 . Так как силы
. Так как силы 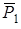 и
и 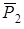 параллельны оси
параллельны оси 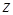 , а реакции
, а реакции 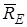 и
и 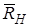 эту ось пересекают, то их моменты относительно оси z равны нулю. Тогда, считая для момента положительным направление
эту ось пересекают, то их моменты относительно оси z равны нулю. Тогда, считая для момента положительным направление 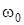 (т.е. против хода часовой стрелки), получаем
(т.е. против хода часовой стрелки), получаем
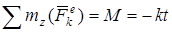 ,
,
и уравнение (1) принимает вид:
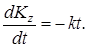 (2)
(2)
Умножая обе части этого уравнения на dt и интегрируя, получим
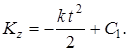 (3)
(3)
Для рассматриваемой механической системы
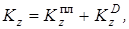 (4)
(4)
где 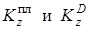 – кинетические моменты относительно оси z платформы и груза D соответственно.
– кинетические моменты относительно оси z платформы и груза D соответственно.
Поскольку платформа вращается вокруг оси z, то ее кинетический момент равен произведению момента инерции относительно оси z на угловую скорость:
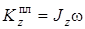 . (5)
. (5)
Значение момента инерции платформы относительно оси z найдем по теореме Гюйгенса:
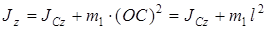 , (6)
, (6)
где 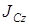 – момент инерции платформы относительно оси Cz, параллельной оси
– момент инерции платформы относительно оси Cz, параллельной оси 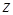 и проходящей через центр масс платформы
и проходящей через центр масс платформы 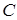 .
.
Момент инерции 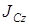 относительно оси, проходящей через центр масс платформы перпендикулярно ее плоскости, равен:
относительно оси, проходящей через центр масс платформы перпендикулярно ее плоскости, равен:

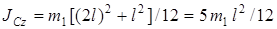 .
.
Тогда

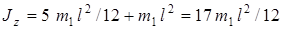 .
.
Следовательно,
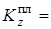
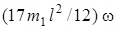 . (7)
. (7)
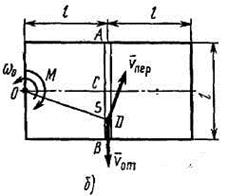
Для определения 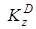 обратимся к рис. Д3б и рассмотрим движение груза
обратимся к рис. Д3б и рассмотрим движение груза 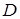 как сложное, считая его движение по платформе относительным движением, а вращение самой платформы вокруг оси z – переносным движением. Тогда абсолютная скорость груза
как сложное, считая его движение по платформе относительным движением, а вращение самой платформы вокруг оси z – переносным движением. Тогда абсолютная скорость груза 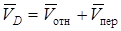 , и по теореме Вариньона,
, и по теореме Вариньона,
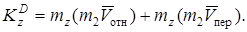 (8)
(8)
Так как груз 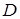 движется по закону
движется по закону 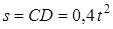 , то
, то
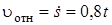 .
.
Изображаем вектор 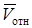 на рис. Д3б с учетом знака
на рис. Д3б с учетом знака 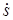 (при
(при 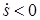 направление
направление 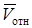 было бы противоположным).
было бы противоположным).
Затем, учитывая направление угловой скорости 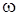 , изображаем вектор переносной скорости
, изображаем вектор переносной скорости 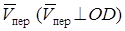 . Модуль переносной скорости равен
. Модуль переносной скорости равен
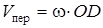 .
.
Тогда равенство (8) примет вид:
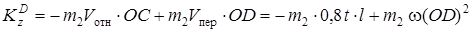 . (9)
. (9)
Но на рис. Д3б видно, что
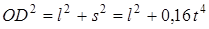 ,
,
тогда
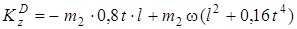 . (10)
. (10)
Подставляя 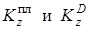 из (7) и (10) в равенство (4), получим с учетом данных задачи:
из (7) и (10) в равенство (4), получим с учетом данных задачи:
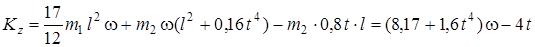 . (11)
. (11)
Тогда уравнение (3), где 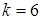 , принимает вид
, принимает вид
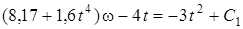 . (12)
. (12)
Постоянную интегрирования определяем из начального условия: при 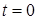
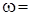
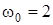 с-1, откуда получаем
с-1, откуда получаем
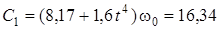 .
.
При этом значении 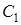 из уравнения (12) находим искомую зависимость w от t.
из уравнения (12) находим искомую зависимость w от t.
Ответ:
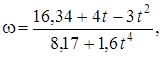
где t – в секундах, w – в с-1.
Задача Д 4
(тема : “Теорема об изменении кинетической энергии системы ”)
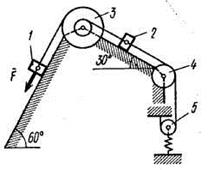
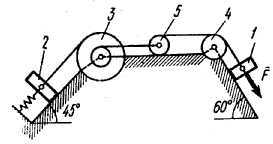
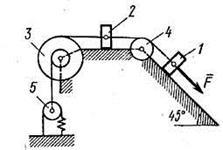
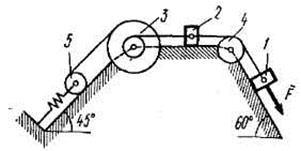
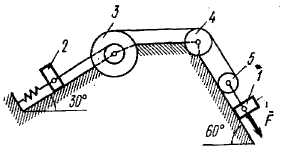
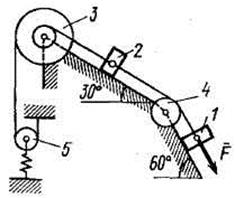
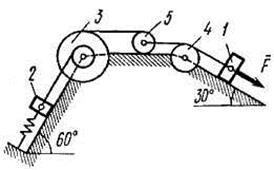
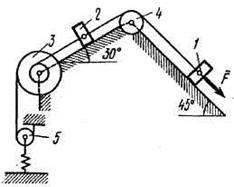
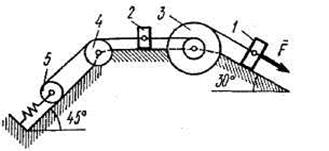
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3 = 0,1 м и радиусом инерции относительно оси вращения 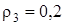 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д4.0-Д4.9, табл. Д4); тело 5 считать сплошным однородным цилиндром (диском), массу блока 4 – равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нерастяжимыми нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с. Массами пружины и нитей пренебречь.
м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д4.0-Д4.9, табл. Д4); тело 5 считать сплошным однородным цилиндром (диском), массу блока 4 – равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нерастяжимыми нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с. Массами пружины и нитей пренебречь.
Под действием силы 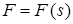 , зависящей от перемещения s точки приложения силы, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении системы на шкив 3 действует постоянный момент M сил сопротивления (от трения в подшипниках).
, зависящей от перемещения s точки приложения силы, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении системы на шкив 3 действует постоянный момент M сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s точки приложения силы 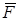 станет равным
станет равным 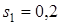 м. Искомая величина указана в столбце "Найти" таблицы, где обозначено:
м. Искомая величина указана в столбце "Найти" таблицы, где обозначено: 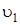 ,
, 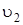 ,
, 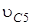 – скорости грузов 1, 2 и центра масс тела 5 соответственно,
– скорости грузов 1, 2 и центра масс тела 5 соответственно, 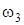 и
и 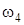 – угловые скорости тел 3 и 4.
– угловые скорости тел 3 и 4.
Все катки, считая и катки, обмотанные нитями (как, например, каток 5 на рис. 2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если 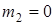 ; остальные тела должны изображаться и тогда, когда их масса равна нулю.
; остальные тела должны изображаться и тогда, когда их масса равна нулю.
Перед выполнением задания прочтите по учебнику тему: «Теорема об изменении кинетической энергии системы».
Ответьте на вопросы:
1. Что такое кинетическая энергия точки и системы?
2. Формулы для вычисления кинетической энергии твердого тела при поступательном, вращательном и плоском движениях.
3. Формулы для вычисления работы силы на бесконечно малом перемещении точки приложения силы (элементарная работа силы; различные формы записи).
4. В каких случаях работа силы равна нулю? Поясните, используя любую формулу для вычисления элементарной работы силы.
5. Вычисление работы силы на конечном перемещении точки приложения силы или за конечное время (полная работа).
6. Формулы для вычисления работы:
а) силы тяжести,
б) упругой силы,
в) пары сил (момента).
7. Сформулируйте теорему об изменении кинетической энергии системы в любой форме и запишите соответствующее уравнение.
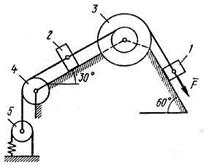
| 
|
| Рис. Д4.0 | Рис. Д4.1 |
| 
|
| Рис. Д4.2 | Рис. Д4.3 |
| 
|
| Рис. Д4.4 | Рис. Д4.5 |
| 
|
| Рис. Д4.6 | Рис. Д4.7 |
| 
|
| Рис. Д4.8 | Рис. Д4.9 |
Таблица Д4
| Номер условия | m1, кг | m2, кг | m3, кг | m4, кг | m5, кг | с, Н / м | M, Н×м | F = f(s), Н | Найти |
| 0 | 0 | 6 | 4 | 0 | 5 | 200 | 1,2 | 80(4+5s) | 
|
| 1 | 8 | 0 | 0 | 4 | 6 | 320 | 0,8 | 50(8+3s) | 
|
| 2 | 0 | 4 | 6 | 0 | 5 | 240 | 1,4 | 60(6+5s) | 
|
| 3 | 0 | 6 | 0 | 5 | 4 | 300 | 1,8 | 80(5+6s) | 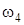
|
| 4 | 5 | 0 | 4 | 0 | 6 | 240 | 1,2 | 40(9+4s) | 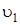
|
| 5 | 0 | 5 | 0 | 6 | 4 | 200 | 1,6 | 50(7+8s) | 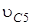
|
| 6 | 8 | 0 | 5 | 0 | 6 | 280 | 0,8 | 40(8+9s) | 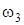
|
| 7 | 0 | 4 | 0 | 6 | 5 | 300 | 1,5 | 60(8+5s) | 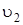
|
| 8 | 4 | 0 | 0 | 5 | 6 | 320 | 1,4 | 50(9+2s) | 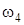
|
| 9 | 0 | 5 | 6 | 0 | 4 | 280 | 1,6 | 80(6+7s) | 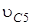
|
Теорема об изменении кинетической энергии механической системы
(краткие сведения из теории)
Кинетическая энергия . Кинетической энергией точки называется величина 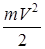 , где m – масса точки, , где m – масса точки, 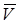 – абсолютная скорость точки. Кинетическая энергия механической системы – абсолютная скорость точки. Кинетическая энергия механической системы
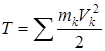 , (1)
где , (1)
где 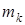 – масса точки системы, – масса точки системы, 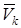 – абсолютная скорость этой точки.
Для твердого тела из (1) следует, что
при поступательном движении твердого тела – абсолютная скорость этой точки.
Для твердого тела из (1) следует, что
при поступательном движении твердого тела
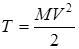 ,
где M – масса тела, ,
где M – масса тела, 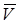 – скорость тела;
при вращении твердого тела вокруг неподвижной оси – скорость тела;
при вращении твердого тела вокруг неподвижной оси
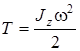 ,
где ,
где 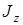 – момент инерции тела относительно оси вращения, w – угловая скорость тела;
при плоском движении тела – момент инерции тела относительно оси вращения, w – угловая скорость тела;
при плоском движении тела
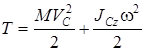 ,
где M – масса тела, ,
где M – масса тела, 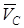 – скорость центра масс тела, – скорость центра масс тела, 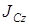 – момент инерции тела относительно оси, проходящей через центр масс С тела, перпендикулярно плоскости сечения, w – угловая скорость тела. – момент инерции тела относительно оси, проходящей через центр масс С тела, перпендикулярно плоскости сечения, w – угловая скорость тела.
|
Момент инерции тела относительно оси z – это величина
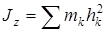 ,
где ,
где 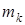 – масса точки тела, – масса точки тела, 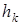 – расстояние от этой точки до оси z.
Момент инерции тела зависит от формы тела и положения оси z. Значения – расстояние от этой точки до оси z.
Момент инерции тела зависит от формы тела и положения оси z. Значения 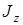 для однородных тел простой формы (кольцо, стержень, диск, прямоугольник, цилиндр и т. д.) приводятся в справочниках по механике; значения для однородных тел простой формы (кольцо, стержень, диск, прямоугольник, цилиндр и т. д.) приводятся в справочниках по механике; значения 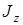 , необходимые для решения данной задачи, приведены ниже в указаниях к решению.
Если задан радиус инерции r тела, то , необходимые для решения данной задачи, приведены ниже в указаниях к решению.
Если задан радиус инерции r тела, то 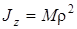 , где M – масса тела.
Элементарная работа силы dA на бесконечно малом перемещении ds точки, в которой приложена сила, равна , где M – масса тела.
Элементарная работа силы dA на бесконечно малом перемещении ds точки, в которой приложена сила, равна
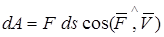 , (2)
где , (2)
где 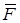 – сила, ds – модуль бесконечно малого перемещения точки, – сила, ds – модуль бесконечно малого перемещения точки, 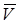 – скорость точки, в которой приложена сила (направление – скорость точки, в которой приложена сила (направление 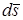 совпадает с направлением совпадает с направлением 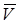 ). Выражение (2) – одна из возможных форм записи ). Выражение (2) – одна из возможных форм записи 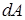 . Например, если учесть, что . Например, если учесть, что 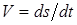 , то из (2) следует еще одна форма записи: , то из (2) следует еще одна форма записи:
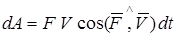 , (3)
где dt – время бесконечно малого перемещения. Из (2) (или (3)) следует, что , (3)
где dt – время бесконечно малого перемещения. Из (2) (или (3)) следует, что
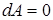 если если 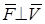 ; ;
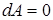 если если 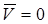 ; ;
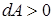 если если 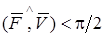 ; ;
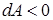 если если 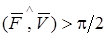 .
Если сила приложена к точке вращающегося тела, то, применяя (2), получим .
Если сила приложена к точке вращающегося тела, то, применяя (2), получим
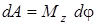 , (4)
где , (4)
где 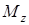 – момент силы относительно оси вращения тела, – момент силы относительно оси вращения тела, 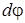 – бесконечно малый угол поворота тела. Если на тело действует пара сил, то (4) дает элементарную работу пары сил, где – бесконечно малый угол поворота тела. Если на тело действует пара сил, то (4) дает элементарную работу пары сил, где 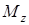 – момент пары сил относительно оси z.
Работа силы на конечном перемещении точки из – момент пары сил относительно оси z.
Работа силы на конечном перемещении точки из 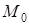 в в 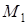
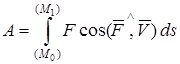 . (5)
Из (5) следуют выражения для работы силы в частных случаях.
Работа силы тяжести (постоянной): . (5)
Из (5) следуют выражения для работы силы в частных случаях.
Работа силы тяжести (постоянной):
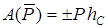 ,
где P=mg – сила тяжести, ,
где P=mg – сила тяжести, 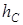 – перемещение центра масс тела по вертикали. Знак “–“ соответствует движению центра масс вверх. – перемещение центра масс тела по вертикали. Знак “–“ соответствует движению центра масс вверх.
|
Работа упругой силы пружины:
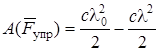 ,
где с – жесткость пружины, ,
где с – жесткость пружины, 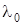 и и 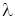 – начальное и конечное удлинение (или сжатие) пружины.
Работа пары сил, приложенной к вращающемуся телу, при повороте тела на угол – начальное и конечное удлинение (или сжатие) пружины.
Работа пары сил, приложенной к вращающемуся телу, при повороте тела на угол 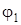 , равна , равна
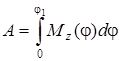 ,
где ,
где 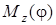 – момент пары сил относительно оси вращения. Если – момент пары сил относительно оси вращения. Если 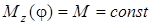 , то , то
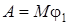 .
Если пара сил препятствует вращению тела, то A<0. .
Если пара сил препятствует вращению тела, то A<0.
|
Теорема об изменении кинетической энергии системы .
Формулировка (в интегральной (конечной) форме): изменение кинетической энергии системы на некотором конечном перемещении системы из одного положения в другое равно сумме работ всех внешних и внутренних сил, приложенных к точкам системы на соответствующих конечных перемещениях точек приложения этих сил.
Математическая запись:
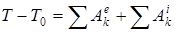 .
Если система состоит из абсолютно твердых тел, соединенных нерастяжимыми нитями или стержнями (неизменяемая система), то .
Если система состоит из абсолютно твердых тел, соединенных нерастяжимыми нитями или стержнями (неизменяемая система), то 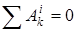 . .
|
Указания. Задача Д4 – на применение теоремы об изменении кинетической энергии системы. При решении задачи учесть, что кинетическая энергия 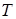 системы равна сумме кинетических энергий всех входящих в систему тел; эту энергию нужно выразить через ту скорость (линейную или угловую), которую в задаче надо определить. При вычислении кинетической энергии катка 5, совершающего плоское движение, для установления зависимости между скоростями его точек или между его угловой скоростью и скоростью центра масс воспользоваться понятием о мгновенном центре скоростей (кинематика). При вычислении работы все перемещения следует выразить через заданное перемещение s1, учитывая, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.
системы равна сумме кинетических энергий всех входящих в систему тел; эту энергию нужно выразить через ту скорость (линейную или угловую), которую в задаче надо определить. При вычислении кинетической энергии катка 5, совершающего плоское движение, для установления зависимости между скоростями его точек или между его угловой скоростью и скоростью центра масс воспользоваться понятием о мгновенном центре скоростей (кинематика). При вычислении работы все перемещения следует выразить через заданное перемещение s1, учитывая, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.
Последовательность действий при решении задачи см. в примере Д4.
Момент инерции шкива, блока или катка массы m относительно оси 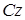 , перпендикулярной пластине и проходящей через ее центр масс
, перпендикулярной пластине и проходящей через ее центр масс 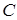 , равен:
, равен:
| для сплошного однородного диска (цилиндра) радиуса R | 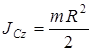 ; ;
|
| для блока, масса которого равномерно распределена по ободу радиуса R | 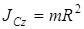 ; ;
|
| для ступенчатого шкива с радиусом инерции r | 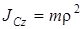 . .
|
Пример Д4. Механическая система (рис. Д4а) состоит из сплошного однородного цилиндрического катка 1, подвижного блока 2, ступенчатого шкива 3 с радиусами ступеней R3 и r3 и радиусом инерции относительно оси вращения 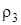 , блока 4 и груза 5 (коэффициент трения груза о плоскость равен
, блока 4 и груза 5 (коэффициент трения груза о плоскость равен 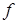 ). Тела системы соединены друг с другом нитями, намотанными на шкив 3. К центру Е блока 2 прикреплена пружина с коэффициентом жесткости с, ее начальная деформация равна нулю; массами нити и пружины пренебречь.
). Тела системы соединены друг с другом нитями, намотанными на шкив 3. К центру Е блока 2 прикреплена пружина с коэффициентом жесткости с, ее начальная деформация равна нулю; массами нити и пружины пренебречь.








