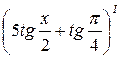Тема 9 Похідна і її застосування.

Дата: 2025-06-02; Просмотры: 7
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

 

Заняття 7. Похідна складеної функції.

Навчальна мета: Навчити диференціювати складну функцію.

Розвивальна мета: Розвивати творчу активність учнів, виховувати інтерес до вивчення математики в процесі виведення та використовування формул диференціювання.

Виховна мета: Виховувати уважність та акуратність.

План

  1. Похідна складної функції.
  2. Похідна оберненої функції. Похідна степеневої функції з раціональним показником.
  3. Розв'язування вправ.

 

Хід заняття

І. Перевірка домашнього завдання.

1. Фронтальне опитування

  1. Чому дорівнює похідна сталої функції?
  2. Чому дорівнює похідна степеневої функції з цілим показником?
  3. Сформулювати теорему про похідну суми (різниці) двох функцій.
  4. Сформулювати теорему про похідну добутку двох (трьох) функцій.
  5. Чому дорівнює похідна добутку двох функцій, у якому один із співмножників сталий?
  6. Сформулювати теорему про похідну частки від ділення двох функцій.

2.Виконати вправи

1.

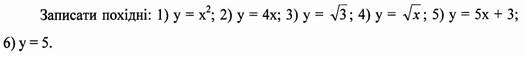
2. Записати похідну суми

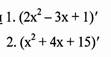
3.Записати похідну добутку

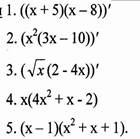
4.Записати похідну частки

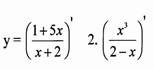
Нові формули в таблицю

II . Сприймання і усвідомлення поняття складеної функції та її похідної.

Теорема. Похідна складеної функції у == f( g( x)) знаходиться за формулою

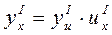де u = g(x),

або похідна складеної функції дорівнює похідній зовнішній функції по проміжній змінній, помноженій на похідну внутрішньої функції по основному аргу­менту.

Доведення

Будемо вважати, що функція u = g( x) має похідну в точці xo, а функція у = f( u) має похідну в точці uo = g( xo), тобто існують границ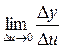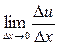і , і

Δu = g( xo + Δx) - g(xo) 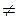0.

Нехай аргументу xo надано приросту Δx, тоді змінна u набуде приросту Δu 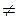0. Поскільки g( x) одержала приріст Δu, то функція у також одержить приріст Δy = f(u + Δu) – f(u). Приріст Δx зумовив виникнення приросту Δu і Δy.

Подамо 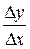= 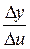· 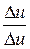. Перейдемо до границі при Δx → 0 (при цьому Δu→0).

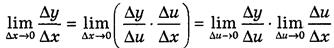
або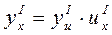

Приклад 1. Знайдіть похідну функції у = (3x3 – 1)5.

Розв'язання

у = (3х3 – 1)5 — складена функція у = u5, де u = 3 x3 – 1, тоді 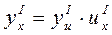y' = ( u5)' · (3х3 – 1)’ = 5 u4 · 9х = 5(3х3 -1)4 · 9х = 45х(3х3 – 1)4.

При обчисленні похідної складеної функції явне введення допоміжної букви u для позначення проміжного аргументу не є обов'язковим. Тому похідну даної функції знаходять відразу як добуток похідної степеневої функції u5 на похідну від функції 3х3 – 1:

у' = ((3x3 – 1)5)' = 5(3х3 -1)4 · (3x3 – 1)' = 5 · (3x3 – 1)4 · 9x = 45x(3x3 – 1)4.

Приклад 2. Знайдіть похідні функцій:

а) у = 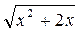; б) у = sin (3х + 5); в) у = cos2x; г) y = cos x2.

Розв'язання

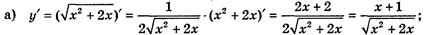
б) у' = (sin(3x + 5))' = cos (3х + 5) · (3x· + 5)' = 3 cos(3x + 5);

в) у = (cos2 x)' = 2 cos x· (cos x )' = 2 cos x · (- sin x ) = = -2 cos x sin x = - sin 2x;

г) y’ = ( cos x2)' = - sin x2 · ( x2)' = -2 x sin x2.

Виконання вправ____________________________

1. Знайдіть похідні функцій:

а) у = (3х + 2)50; б) у = (6 - 7х)10; в) у = 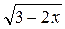; г) у = .

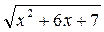Відповідь: а) у' = 150 · (3х + 2)49; б) у' = -70 · (6 – 7x)9;

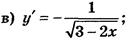
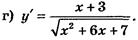
2. Знайдіть похідні функцій:

а) у' = cos 6x; б) y = sin3 x; в) у = 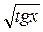, г) у = ctg x4.

Відповідь : а) у' = -6 sin 6х; б) у' = 3sin2 x cos x;

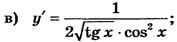
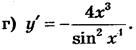
IV. Домашнє завдання.

Зробити конспект та виконати завдання

№ 10. Знайдіть похідні функцій

6) y ' = ((l + sin x)2)';

10) у’ = ( )’ ;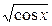

14) у' = (ctg3 x)’ .

22) y’ =