Метод нормированных значений.
В реальных условиях при наличии теплоотдачи температура двигателя за время 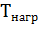 повысится лишь до значения
повысится лишь до значения  = 0,632
= 0,632 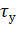 . Это следует из уравнения (7.11). Если в нем положить t =
. Это следует из уравнения (7.11). Если в нем положить t = 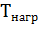 , то
, то
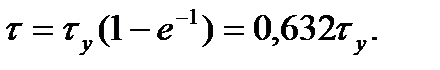 (7.17)
(7.17)
Указанным соотношением пользуются для определения значения постоянной времени нагрева, если известна полученная опытным путем кривая нагрева двигателя. В этом случае на кривой  = f(t) находят точку
= f(t) находят точку  = 0,бЗ2
= 0,бЗ2 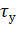 , и значение
, и значение 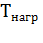 определяют отрезком, лежащим между началом координат и перпендикуляром, опущенным на ось абсцисс из указанной точки, как это показано на рис.7.6.
определяют отрезком, лежащим между началом координат и перпендикуляром, опущенным на ось абсцисс из указанной точки, как это показано на рис.7.6.
Метод касательной.
Второй, графический метод определения 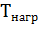 основан на следующем: если провести касательную к экспоненциальной кривой
основан на следующем: если провести касательную к экспоненциальной кривой  = f (t) до пересечения с асимптотой, то отрезок, заключенный между точкой пересечения на асимптоте и перпендикуляром, проведенным через точку касания, равен постоянной времени нагрева. Это легко прослеживается, например, для касательной, проведенной к кривой
= f (t) до пересечения с асимптотой, то отрезок, заключенный между точкой пересечения на асимптоте и перпендикуляром, проведенным через точку касания, равен постоянной времени нагрева. Это легко прослеживается, например, для касательной, проведенной к кривой  = f(t) в точке 0, как видно на рис.7.6, где отрезок DE равен
= f(t) в точке 0, как видно на рис.7.6, где отрезок DE равен 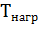 .
.
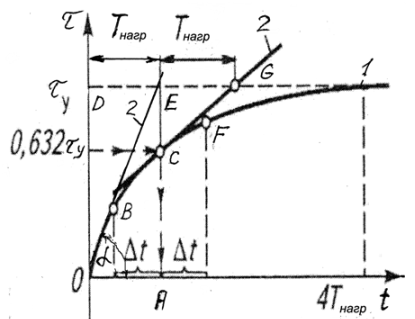
Рис. 7.6. Графические построения для определения постоянной времени нагрева электродвигателя: 1- кривая нагрева двигателя;
2 – касательные.
Для доказательства возьмем первую производную выражения
( 7.11) по времени
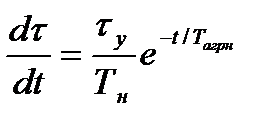
Для t = 0
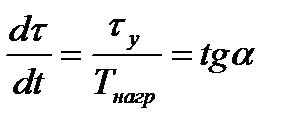
откуда
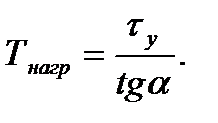
Из рис.7.6 видно, что 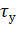 = А E , tg а = А E /0А. Но ОА = DE,
= А E , tg а = А E /0А. Но ОА = DE,
поэтому 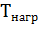 = DE.
= DE.
Следует отметить, что получение графическим методом значения постоянной времени нагрева возможно также при проведении касательной в любой точке экспоненциальной кривой. Например, проводя касательную через точку F, получаем отрезок EG = 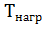 (рис.7.6).
(рис.7.6).
Из многочисленных экспериментов известно, что кривая нагрева отличается от теоретической. В начале процесса нагрева действительное повышение температуры двигателя идет быстрее, чем это предусматривается теоретической кривой. Только, при температурах от 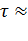 (0,5 + 0,6)
(0,5 + 0,6)  до
до  =
= 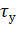 действительная кривая нагрева приближается к экспоненциальной. Отклонение кривой нагрева от экспоненты в начале процесса приводит к тому, что определение постоянной времени нагрева в любой точке является ненадежным.
действительная кривая нагрева приближается к экспоненциальной. Отклонение кривой нагрева от экспоненты в начале процесса приводит к тому, что определение постоянной времени нагрева в любой точке является ненадежным.
Постоянная времени нагрева оказывается большей у двигателей закрытого исполнения, габариты которых при прочих равных условиях получаются большими вследствие худших условий теплоотдачи.
Аналитический метод.
Хорошие результаты при расчете постоянной времени нагрева по паспортным данным двигателей получаются при использовании формулы, рекомендованной Шичковым Л.П. [23].
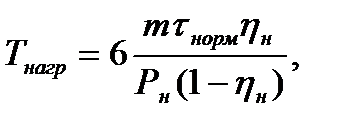 (7.18)
(7.18)
где т - масса электродвигателя, кг; 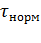 - среднее установившееся превышение температуры двигателя при номинальной нагрузке при измерении методом сопротивления, град: 60 - для изоляции класса А, 75 - для класса Е,80 - для класса В,100 - для класса Р и 125 - для класса Н. Класс изоляции указывают на паспортном щитке электродвигателя;
- среднее установившееся превышение температуры двигателя при номинальной нагрузке при измерении методом сопротивления, град: 60 - для изоляции класса А, 75 - для класса Е,80 - для класса В,100 - для класса Р и 125 - для класса Н. Класс изоляции указывают на паспортном щитке электродвигателя; 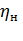 - номинальный (паспортный) КПД двигателя;
- номинальный (паспортный) КПД двигателя; 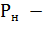 номинальная (паспортная) мощность двигателя, Вт.
номинальная (паспортная) мощность двигателя, Вт.
Метод трех точек.
Постоянную времени нагрева двигателя можно определить по методу трех точек. При использовании этого метода необязательно знать установившееся превышение температуры. Достаточно иметь участок кривой нагрева и выбрать на нем через равные интервалы времени три точки B, C и F, которые соответствуют значениям температур (рис.7.6). Постоянную времени нагрева рассчитывают по формуле:
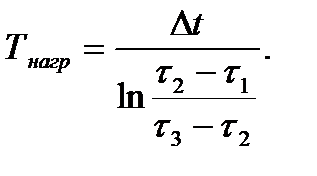 (7.19)
(7.19)
При определении постоянной охлаждения 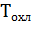 по кривой охлаждения отключенного двигателя следует помнить, что, используя метод нормированного значения, значение 0,632
по кривой охлаждения отключенного двигателя следует помнить, что, используя метод нормированного значения, значение 0,632 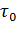 откладывают вниз от начального значения‚ при t = 0. При пользовании методом касательной необходимо учесть, что при охлаждении
откладывают вниз от начального значения‚ при t = 0. При пользовании методом касательной необходимо учесть, что при охлаждении 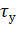 = 0. Поэтому отрезок
= 0. Поэтому отрезок 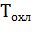 получится на оси времени. Метод трех температур сохраняется без изменения, если превышения температуры откладывают по кривой охлаждения последовательно, по мере остывания двигателя, через равные интервалы времени
получится на оси времени. Метод трех температур сохраняется без изменения, если превышения температуры откладывают по кривой охлаждения последовательно, по мере остывания двигателя, через равные интервалы времени 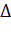 t.
t.
Для получения зависимости  = f(t) при охлаждении двигателя от
= f(t) при охлаждении двигателя от 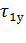 до
до 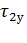 можно воспользоваться выражением (7.10), подставляя в него
можно воспользоваться выражением (7.10), подставляя в него 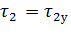 и
и 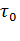 =
= 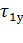 , получают:
, получают:
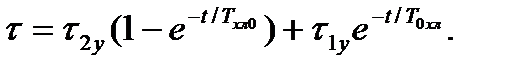 (7.20)
(7.20)
В частном случае, когда охлаждение двигателя совершается до температуры окружающей среды, т. е. 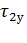 = 0, уравнение (7.20)
= 0, уравнение (7.20)
приобретает вид:
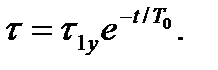 (7.21)
(7.21)
При рассмотрении рис.7.5 видно, что для одной и той же постоянной времени кривая охлаждения приближенно представляет собой зеркальное отражение кривой нагрева. Равенство постоянных времени нагрева и охлаждения может быть у двигателя с независимой вентиляцией, где теплоотдача двигателя во время работы и при остановке одинакова. Для самовентилируемых двигателей постоянная времени охлаждения больше постоянной времени нагрева примерно в 2…З раза по причине ухудшения условий теплоотдачи.
Постоянные времени нагрева и охлаждения можно определить различными экспериментальными методами, которые справедливы также для экспериментального нахождения постоянных времени электрических и механических переходных процессов.
Отношение теплоотдачи двигателя в неподвижном состоянии 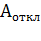 к теплоотдаче двигателя при вращении
к теплоотдаче двигателя при вращении 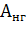 называют
называют
коэффициентом охлаждения
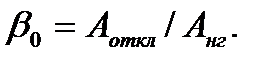 (7.22)
(7.22)
На основании (7.16) и (7.22) получают соотношение, связывающее постоянные времени нагрева 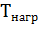 и охлаждения
и охлаждения 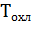 двигателя:
двигателя:
 =
= 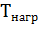 /
/  (7.23)
(7.23)
Коэффициент 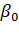 для электродвигателей различного исполнения имеет значения: закрытого, без наружного охлаждения или с принудительной независимой вентиляцией - 0,9... 1; закрытого, с наружным охлаждением от собственного вентилятора на валу двигателя - 0,45...0,55; защищенный, с вентиляцией от собственного вентилятора на валу двигателя - 0,25.. .0,35.
для электродвигателей различного исполнения имеет значения: закрытого, без наружного охлаждения или с принудительной независимой вентиляцией - 0,9... 1; закрытого, с наружным охлаждением от собственного вентилятора на валу двигателя - 0,45...0,55; защищенный, с вентиляцией от собственного вентилятора на валу двигателя - 0,25.. .0,35.
Правильный выбор мощности двигателя предполагает соблюдение условия, при котором установившаяся температура равна допустимой, т. е.
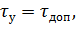
где 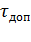 - допустимое превышение температуры, определяемое
- допустимое превышение температуры, определяемое
классом изоляции, примененной в двигателе.
При различных нагрузках нагревание двигателя происходит по разным кривым, как это показано на рис.7.7. Постоянная времени нагрева двигателя остается неизменной, чему отвечают равные отрезки на соответствующих асимптотах. Значения установившихся температур 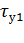 ,
, 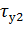 ,
, 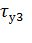 расположены тем выше, чем больше нагружен двигатель [22]. Это и понятно, так как большей нагрузке соответствуют большие потери.
расположены тем выше, чем больше нагружен двигатель [22]. Это и понятно, так как большей нагрузке соответствуют большие потери.
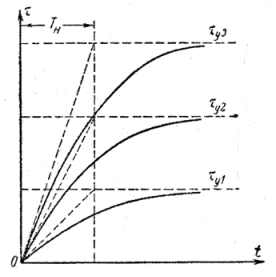
Рис.7.7. Кривые нагрева электродвигателя при различной
продолжительности нагрузки.
Значение установившейся температуры пропорционально потерям в двигателе  = Q/A.
= Q/A.
Если нагрузка двигателя во время работы изменяется, то изменяется и количество теплоты, выделяемое в разные периоды времени, чему соответствуют различные отрезки экспоненциальных кривых нагрева и охлаждения. При переменной нагрузке кривая нагрева (рис.7.8) будет ломаной. С увеличением нагрузки растут потери и температура двигателя. При снижении ее, например, до значения, обусловленного холостым ходом, потери уменьшаются и температура двигателя соответственно снижается. Таким образом, при переменной нагрузке температура двигателя непрерывно изменяется.
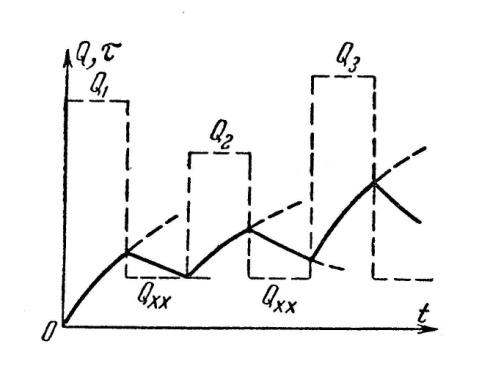
Рис.7.8. Изменение температуры электродвигателя
при переменной нагрузке.
7.3. Параметры, влияющие на мощность двигателя
при его подборе
В номинальном режиме работы потери мощности 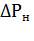 электродвигателя связаны с мощностью на валу
электродвигателя связаны с мощностью на валу 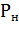 через номинальный КПД:
через номинальный КПД:
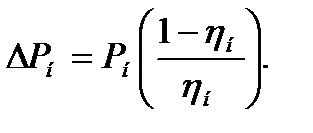 (7.24)
(7.24)
На основании (7.12) номинальные потери мощности можно
записать:
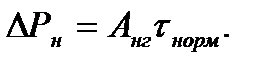
Приравнивая правые части выражений (7.23) и (7.24), получим:
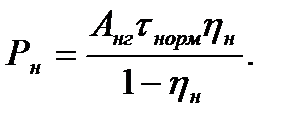 (7.25 )
(7.25 )
В выражение (7.25) входят основные параметры, влияющие на мощность электродвигателя: теплоотдача двигателя при работе (нагрузке) 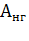 нормированное (предельно допускаемое) превышение температуры
нормированное (предельно допускаемое) превышение температуры 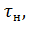 зависящее от нагревостойкости изоляции двигателя, и номинальный КПД двигателя. Для повышения мощности электродвигателя при сохранении его габаритных размеров и расхода активных материалов, идущих на его изготовление, необходимо:
зависящее от нагревостойкости изоляции двигателя, и номинальный КПД двигателя. Для повышения мощности электродвигателя при сохранении его габаритных размеров и расхода активных материалов, идущих на его изготовление, необходимо:
увеличивать теплоотдачу двигателя, т.е. улучшать условия охлаждения. Для этого корпуса двигателей закрытого исполнения делают ребристыми, а у двигателей защищенного исполнения предусматривают вентиляционные каналы; применяют принудительный обдув от собственного вентилятора, а для крупных двигателей - и от отдельного, специально для этого предназначенного;
повышать нормированное превышение температуры, т.е. использовать более нагревостойкую изоляцию при изготовлении двигателя;
повышать КПД двигателя за счет технологически чистой меди, идущей на изготовление обмоток, за счет применения высоколегированной текстурованной (холоднокатаной) стали, образующей
магнитную систему двигателя, и т. д.
Номинальную нагрузку электродвигателя рациональнее устанавливать по нормированному превышению температуры чем по нормированной температуре. Поэтому установлены нормы не только на предельно допускаемые температуры нагрева изоляции разных классов, но и на предельно допускаемые превышения
температуры изоляции.
Для измерения температуры в доступных местах применяют термометры. Но термометром нельзя измерить температуру внутренних, наиболее нагретых, частей обмотки. Другой способ измерения, называемый методом сопротивления, состоит в определении средней температуры обмотки по изменению ее омического сопротивления при нагревании.
Если сопротивление обмотки, измеренное в холодном состоянии при температуре окружающей среды 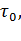 равно
равно 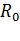 , то при работе двигателя сопротивление, возрастая пропорционально перегреву
, то при работе двигателя сопротивление, возрастая пропорционально перегреву 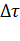 , станет равным
, станет равным 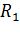 . Зная значение температурного коэффициента изменения сопротивления
. Зная значение температурного коэффициента изменения сопротивления 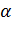 (для меди
(для меди 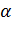 = 1/235, а для алюминия
= 1/235, а для алюминия
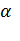 = 1/245 1/Ом), можно определить перегрев.
= 1/245 1/Ом), можно определить перегрев.
Например, для медной обмотки:
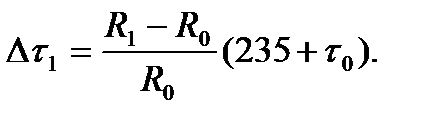 (7.26)
(7.26)
Предельно допустимую рабочую температуру изоляции ( 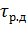 ) определяют как сумму предельно допустимого перегрева и температуры окружающей среды (по стандарту):
) определяют как сумму предельно допустимого перегрева и температуры окружающей среды (по стандарту):
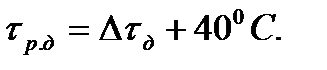 (7.27)
(7.27)
Нормированные значения температуры нагрева 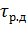 и нормированные превышения температуры
и нормированные превышения температуры 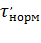 изоляции, наиболее широко используемой для обмоток электрических машин переменного и постоянного тока, приведены в таблице 7.2. Из данных таблицы 7.2 видно, что предельно допустимые значения температур обмоток на 5…10° ниже действительных предельных температур для данных классов изоляции. Это объясняется тем, что методы определения температуры не гарантируют получения максимальных значений
изоляции, наиболее широко используемой для обмоток электрических машин переменного и постоянного тока, приведены в таблице 7.2. Из данных таблицы 7.2 видно, что предельно допустимые значения температур обмоток на 5…10° ниже действительных предельных температур для данных классов изоляции. Это объясняется тем, что методы определения температуры не гарантируют получения максимальных значений
в отдельных точках обмоток.
Таблица 7.2
Нормированные значения превышения температуры в зависимости от
класса нагревостойкости изоляции двигателей
| Показатели нагрева | Класс нагревостойкости изоляции | ||||
| А | Е | В | F | H | |
| Нормированное превышение температуры при измерении методом сопротивления, град | 60 | 75 | 80 | 100 | 125 |
| Нормированное превышение температуры при измерении методом термометра, град | 50 | 65 | 70 | 85 | 105 |
Если температура окружающей среды ниже +40°С, то нагрузку электродвигателя увеличивать не следует. Объясняется это тем, что при большей разности температур между температурой электрической машины и температурой окружающей среды, превышающей значение норм, происходит не тепловой износ изоляции, а физический, который вызывает ее разрушение силами теплового напряжения. Тепловой износ изоляции имеет место лишь при значительных температурах электрической машины. Таким образом, номинальная мощность, указываемая на паспортном щитке электродвигателя, предельна с точки зрения допустимого нагрева двигателя и диктуется классом нагревостойкости используемой в двигателе изоляции.
На основании (7.25) и данных таблицы 7.2 можно сделать вывод, что при применении в электродвигателях более нагревостойкой изоляции повышается их мощность без изменения массогабаритных показателей, а соответственно без увеличения расхода активных материалов, идущих на их изготовление. Например, при применении изоляции класса нагревостойкости Н вместо изоляции класса А мощность электродвигателя повышается примерно в 2 раза.
Современные электродвигатели основного (базового) исполнения в соответствии с ГОСТ51689-2000 могут иметь сервис-фактор, равный 1,1 или 1,15, т.е. допускать длительную перегрузку на 10 и 15% соответственно при номинальных напряжениях и частоте. При этом превышение температуры обмоток двигателей будет не более допустимого на 10%. Двигатели могут работать длительно при температуре окружающей среды, превышающей максимальную рабочую. В этом случае во избежание недопустимого превышения температуры обмоток отдаваемая двигателем мощность должна быть снижена до следующих значений приведенных в табл. 7.3.
Таблица 7.3.
Зависимость отдаваемой мощности электродвигателя от температуры
окружающей среды
Температура
окружающей среды,  С С
| 40 | 45 | 50 | 55 | 60 |
| Отдаваемая мощность,% | 100 | 96 | 92 | 87 | 82 |
Двигатели, имеющие сервис-фактор 1,15, допускают длительную эксплуатацию при номинальной мощности и номинальном напряжении при температуре окружающей среды до +50  С. В соответствии с ГОСТ 28173 (МЭК 34-1): двигатели выдерживают 1,5 кратную перегрузку по току в течение 2 минут; могут эксплуатироваться при отклонении напряжения +5% или отклонении частоты +2% и одновременных отклонениях напряжения и частоты, ограниченных зоной «А» (рис.7.9 ), при этом параметры двигателей могут отличаться от номинальных, а превышения температуры обмоток могут быть более предельных на 10
С. В соответствии с ГОСТ 28173 (МЭК 34-1): двигатели выдерживают 1,5 кратную перегрузку по току в течение 2 минут; могут эксплуатироваться при отклонении напряжения +5% или отклонении частоты +2% и одновременных отклонениях напряжения и частоты, ограниченных зоной «А» (рис.7.9 ), при этом параметры двигателей могут отличаться от номинальных, а превышения температуры обмоток могут быть более предельных на 10  С;
С;
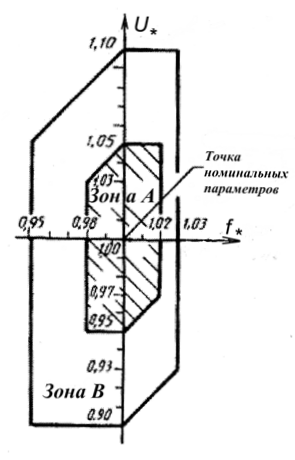
Рис.7.9. Предельные значения напряжения U и частоты f для
электродвигателей в относительных единицах.
Двигатели могут стабильно работать при отклонении напряжения +10% или отклонении частоты от +3 до -5% и одновременных отклонениях напряжения и частоты, ограниченных зоной «В» ( Рис.7.9), продолжительность работы двигателей в крайних пределах зоны «В» рекомендуется ограничивать.
7.4. Расчет мощности двигателя по допустимому нагреву
Мощность электрического привода зависит от мощности используемого в его составе двигателя, который должен иметь в процессе работы допустимую температуру нагрева, надежно запускаться при возможных снижениях питающего напряжения, устойчиво работать при возникновении различных внешних возмущений.
Основой расчета мощности электродвигателя привода в любом режиме работы служит его нагрузочная диаграмма, которая показывает изменение выбранного показателя нагрузки L двигателя в течение характерного периода времени, т.е. нужно иметь зависимость L = f(t). Показателем нагрузки L могут быть: ток 1 потребляемый двигателем; момент нагрузки М на его валу; мощность Р на валу или потребляемая двигателем из сети (рис. 7.10 ).
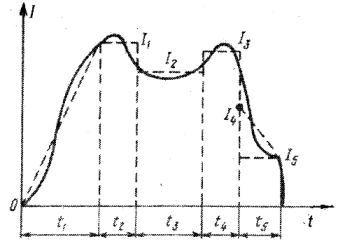
Рис.7.10. Нагрузочная диаграмма электродвигателя.
Нагрузочные диаграммы ЭП обычно получают экспериментальным путем, регистрируя изменения мощности или тока с помощью самопишущих приборов. Иногда диаграммы строят с помощью обычных ваттметров или амперметров, записывая их показания через определенные промежутки времени. В нагрузочной диаграмме, полученной с помощью самопишущего ваттметра, учтены и потери в электродвигателе. Поэтому для получения зависимости полезной мощности от времени необходимо вводить поправку на значение этих потерь, умножая ординаты графика на КПД электродвигателя при данной нагрузке. Если диаграмма построена расчетным путем, такая поправка не вводится. Нагрузочные диаграммы электродвигателей служат основой дня определения мощности, так как только с их помощью выявляются действительные условия работы электродвигателя. Полученную произвольную нагрузочную диаграмму (обычно криволинейную) заменяют одной из номинальных, характеризующих
режим работы S1…S8.
Значение и продолжительность той или иной нагрузки ЭП определяются технологическим процессом. Для хорошо изученных машин и механизмов нагрузки рассчитывают по соответствующим формулам, приводимым в справочной литературе [11].
В случае изменяющейся нагрузочной диаграммы, которую невозможно заменить номинальной (стандартной) используют методы эквивалентных величин. При этом на основании нагрузочной диаграммы рассчитывают эквивалентную нагрузку, действующую на валу двигателя ЭП. Далее с учетом возможных технологических пауз в работе ЭП рассчитывают требуемый номинальный показатель нагрузки электродвигателя:
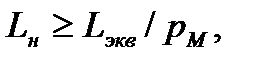 (7.28)
(7.28)
где 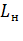 - номинальный показатель нагрузки двигателя;
- номинальный показатель нагрузки двигателя; 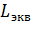 - эквивалентный показатель нагрузочной диаграммы;
- эквивалентный показатель нагрузочной диаграммы; 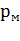 - коэффициент механической (токовой
- коэффициент механической (токовой 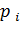 =
= 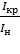 перегрузки двигателя,
перегрузки двигателя, 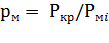 ,
, 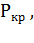 (
( 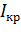 ) - кратковременно допускаемая мощность (ток) двигателя,
) - кратковременно допускаемая мощность (ток) двигателя, 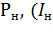 ) - номинальная мощность (ток) двигателя.
) - номинальная мощность (ток) двигателя.
Эквивалентный показатель нагрузочной диаграммы определяют по формуле
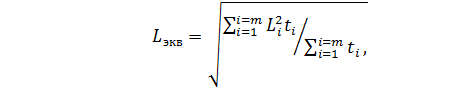 (7.29)
(7.29)
где 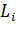 ,
, 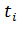 - значения показателя и продолжительности нагрузки для
- значения показателя и продолжительности нагрузки для
i – го участка нагрузочной диаграммы ЭП; n - число участков нагрузочной диаграммы.
При постоянной нагрузке 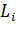 ее значение для одного участка нагрузки (n = 1) совпадает с эквивалентным значением
ее значение для одного участка нагрузки (n = 1) совпадает с эквивалентным значением 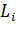 =
= 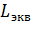 .
.
В длительном режиме работы S1, когда продолжительность непрерывной работы двигателя ЭП превышает 90 мин и двигатель полностью использован по нагреву, достигнув установившейся
температуры, значение коэффициента 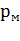 = 1.
= 1.
Если режим работы электродвигателя отличается от длительного S1, то с учетом возможных технологических пауз в работе его коэффициент механической (токовой) перегрузки 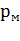 рассчитывают через коэффициент тепловой перегрузки
рассчитывают через коэффициент тепловой перегрузки 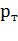 , который представляет собой отношение повышенных кратковременных потерь мощности
, который представляет собой отношение повышенных кратковременных потерь мощности 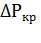 в двигателе к его номинальным
в двигателе к его номинальным 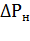 , т.е.
, т.е. 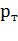 =
= 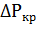 /
/ 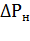 . На основании (7.12) коэффициент тепловой перегрузки двигателя можно выразить в виде:
. На основании (7.12) коэффициент тепловой перегрузки двигателя можно выразить в виде:
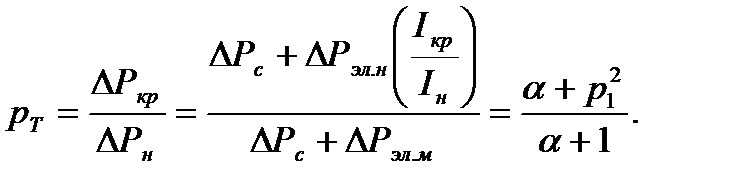 (7.30)
(7.30)
Из (7.30) получаем взаимосвязь между коэффициентами
механической (токовой) и тепловой перегрузок:
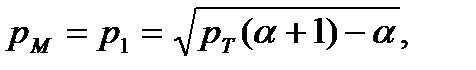 (7.31)
(7.31)
где 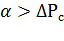 /
/ 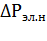 - отношение постоянных потерь мощности в двигателе к номинальным переменным (электрическим потерям),
- отношение постоянных потерь мощности в двигателе к номинальным переменным (электрическим потерям),
С учетом занижения неустановившихся расчетных температур двигателя по общей теории нагрева из-за принятых допущений целесообразно для компенсации возникающей погрешности считать, что все потери мощности в электродвигателе переменные. То есть 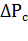 = 0 и
= 0 и 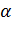 = 0. Тогда выражение (7.31) можно привести к более
= 0. Тогда выражение (7.31) можно привести к более
простому виду:
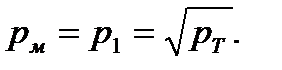 (7.32)
(7.32)
Если в общем случае периоды нагрузки электродвигателя чередуются с его периодическими отключениями, то при правильно выбранной мощности двигателя его превышение температуры должно изменяться от некоторого начального значения 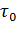 до нормированного для соответствующего класса нагревостойкости изоляции. Исходя из этого и используя формулы (7.10) и (7.21) с учетом соотношения (7.23), можно записать:
до нормированного для соответствующего класса нагревостойкости изоляции. Исходя из этого и используя формулы (7.10) и (7.21) с учетом соотношения (7.23), можно записать:
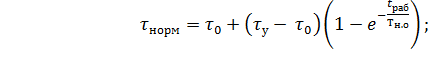 (7.33)
(7.33)
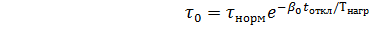 .
.
Учитывая, что 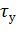 /
/ 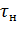 =
= 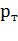 =
= 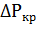 /
/ 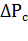 из выражений (7.33) получим формулу расчета коэффициента тепловой
из выражений (7.33) получим формулу расчета коэффициента тепловой
перегрузки в общем виде:
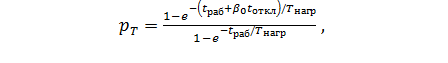 (7.34)
(7.34)
где е - основание натуральных логарифмов, e = 2,718; 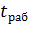 ,
, 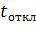 - продолжительности соответственно работы и отключенного состояния электродвигателя или работы на холостом ходу для режима S6, мин;
- продолжительности соответственно работы и отключенного состояния электродвигателя или работы на холостом ходу для режима S6, мин; 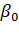 = 0,5 - коэффициент, учитывающий ухудшение теплоотдачи самовентилируемых двигателей закрытого обдуваемого исполнения в отключенном состоянии (при работе на холостом ходу в режиме S6
= 0,5 - коэффициент, учитывающий ухудшение теплоотдачи самовентилируемых двигателей закрытого обдуваемого исполнения в отключенном состоянии (при работе на холостом ходу в режиме S6 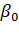 = 1);
= 1); 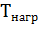 - постоянная времени нагрева электродвигателя, мин. Для большинства электродвигателей постоянная времени нагрева
- постоянная времени нагрева электродвигателя, мин. Для большинства электродвигателей постоянная времени нагрева 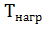 = 15...25 мин и при предварительном расчете мощности двигателя по допустимому нагреву её можно принять на уровне
= 15...25 мин и при предварительном расчете мощности двигателя по допустимому нагреву её можно принять на уровне 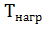 = 20 мин. После выбора электродвигателя
= 20 мин. После выбора электродвигателя
среднее значение постоянной времени нагрева (мин) может быть уточнено по формуле (7.18).
Переход от коэффициента тепловой перегрузки 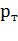 к коэффициентам токовой
к коэффициентам токовой 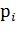 и механической
и механической 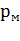 перегрузок ведут по формулам (7.31), (7.32), а определение необходимой мощности электродвигателя по соотношению (7.28) с предварительным расчетом
перегрузок ведут по формулам (7.31), (7.32), а определение необходимой мощности электродвигателя по соотношению (7.28) с предварительным расчетом
эквивалентной мощности нагрузки по (7.29).
Для кратковременного режима работы S2, когда в течение технологических пауз в работе электродвигатель полностью охлаждается до температуры окружающей среды, то есть t 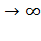 , то по формуле (7.34) получим более простое соотношение:
, то по формуле (7.34) получим более простое соотношение:
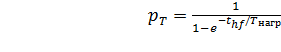 . (7.35)
. (7.35)
В длительном режиме работы S1 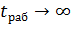 и согласно (7.34 )
и согласно (7.34 )
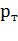 = 1, т.е. электродвигатель не допускает тепловой перегрузки.
= 1, т.е. электродвигатель не допускает тепловой перегрузки.
Окончательно правильность расчета по методу эквивалентных величин уточняют по методу средних потерь. Для правильно выбранного по допустимому нагреву электродвигателя должно выполняться условие:
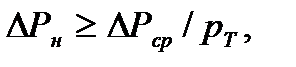 (7.36)
(7.36)
где 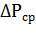 - средние потери мощности в двигателе при работе, Вт;
- средние потери мощности в двигателе при работе, Вт;
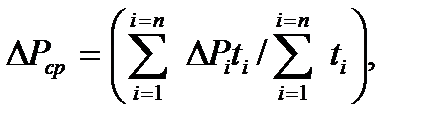 (7.37)
(7.37)
где 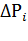 ,
, 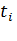 - потери мощности и продолжительность нагрузки двигателя на i-м участке нагрузочной диаграммы.
- потери мощности и продолжительность нагрузки двигателя на i-м участке нагрузочной диаграммы.
Потери мощности на участках нагрузочной диаграммы, преобразованной к виду Р = f(t), равны:
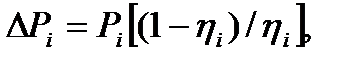 (7.38)
(7.38)
где 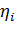 - частичный КПД электродвигателя при
- частичный КПД электродвигателя при 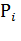 нагрузке на валу, определяют по рабочей характеристике двигателя
нагрузке на валу, определяют по рабочей характеристике двигателя 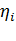 = f(
= f( 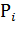 /
/ 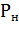 ) или при отсутствии таковой рассчитывают по формуле
) или при отсутствии таковой рассчитывают по формуле
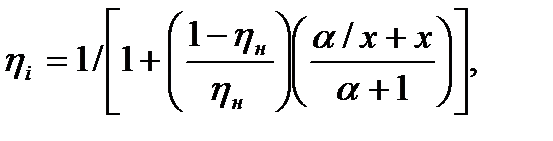 (7.39)
(7.39)
где 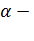 отношение постоянных потерь мощности в двигателе к его номинальным переменным потерям (коэффициент потерь),
отношение постоянных потерь мощности в двигателе к его номинальным переменным потерям (коэффициент потерь),
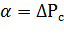 /
/ 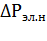 : для электродвигателей общего назначения 0,5...0,7, для крановых 0,6..1,0; х - степень загрузки двигателя, х =
: для электродвигателей общего назначения 0,5...0,7, для крановых 0,6..1,0; х - степень загрузки двигателя, х = 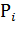 /
/ 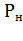 .
.
Постоянные потери мощности 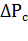 , которые выделяются в двигателе при работе на холостом ходу (
, которые выделяются в двигателе при работе на холостом ходу ( 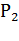 = 0,
= 0, 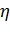 = 0) и которые необходимо учитывать, например в режиме S6 при расчете средних потерь по (7.37), рассчитывают по формуле
= 0) и которые необходимо учитывать, например в режиме S6 при расчете средних потерь по (7.37), рассчитывают по формуле
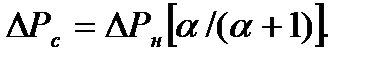 (7.40)
(7.40)
Для повышения точности теплового расчета мощности АД общего применения продолжительного режима S1 для использования в кратковременном S2 или повторно-кратковременном S3 режимах работы целесообразно воспользоваться номограммой рис.7.11, рассчитанной с учетом непостоянства тепловых параметров АД [23]. При этом установившееся значение 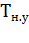 , рассчитывают по среднему значению
, рассчитывают по среднему значению 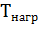 определяемому по формуле (7.18):
определяемому по формуле (7.18): 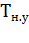 = 4/З
= 4/З 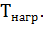
Порядок пользования номограммой для определения коэффициентов перегрузок показан пунктирными линиями. Необходимую мощность двигателя ЭП рассчитывают на основании обобщенной расчетной формулы (7.28) с использованием эквивалентной (средней квадратической) мощности, определенной по нагрузочной
диаграмме двигателя.
Рис.7.11.Номограмма для определения коэффициентов перегрузки асинхронных двигателя режима S1 при работе в режимах S2 и S3.
При использовании специальных электродвигателей, когда в режим работы S2 ставится двигатель режима S2, в режим S3 двигатель режима S3, а в режим S6 - двигатель режима S6, номинальную мощность 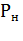 двигателя ведется по формулам соответственно:
двигателя ведется по формулам соответственно:
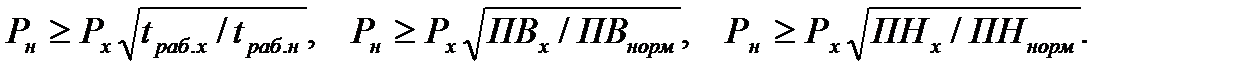 (7.41)
(7.41)
где 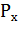 - эквивалентная мощность на валу двигателя за период нагрузки;
- эквивалентная мощность на валу двигателя за период нагрузки; 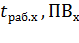 ,
, 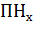 - длительность рабочего периода по нагрузочной диаграмме;
- длительность рабочего периода по нагрузочной диаграмме; 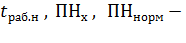 длительность рабочего
длительность рабочего
периода стандартная (нормированная).
В случае использования электродвигателя длительного режима нагрузки S1 в повторно-кратковременном режиме S3 его можно трактовать как электродвигатель режима нагрузки S3 со стандартным значением 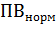 = 100 %. При этом необходимо учитывать ухудшение теплоотдачи двигателя в отключенном состоянии и при перерасчете по формуле (7.41) пользоваться так называемой приведенной продолжительностью включения с использованием значения коэффициента
= 100 %. При этом необходимо учитывать ухудшение теплоотдачи двигателя в отключенном состоянии и при перерасчете по формуле (7.41) пользоваться так называемой приведенной продолжительностью включения с использованием значения коэффициента 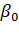 :
:
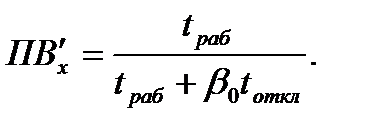 (7.42 )
(7.42 )
Тогда на основании (7.41) получим:
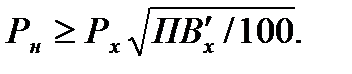 (7.43 )
(7.43 )
Метод эквивалентного тока основан на замене действительно изменяющегося тока в электродвигателе таким эквивалентным током, который вызывал бы те же потери, что и действительный ток. Используя криволинейную токовую нагрузочную диаграмму I=f(t), приведенную на рис. 7.10, разбивают ее на прямолинейные участки и находят эквивалентный ток на каждом участке. для трех прямоугольных участков 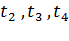 эквивалентный ток определяют по формуле
эквивалентный ток определяют по формуле
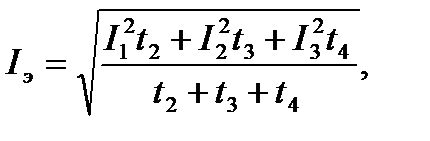 (7.44)
(7.44)
для участков, имеющих вид треугольника (первый участок),
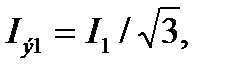 I (7.45)
I (7.45)
для участков, имеющих вид трапеции (пятый участок),
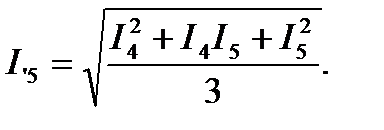 (7.46)
(7.46)
По формулам (7.44), (7.45), (7.46) можно вычислять эквивалентные токи при любом заданном графике тока, представляя его в виде прямоугольников, треугольников и трапеций. После определения
эквивалентного тока проверяют выполнение условия
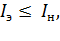 где
где 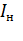 - номинальный ток электродвигателя.
- номинальный ток электродвигателя.
Затем электродвигатель проверяют по допускаемой перегрузке
Если в рассматриваемый цикл работы входят пауза, пуск и торможение электродвигателя, то, учитывая ухудшение условий охлаждения за время паузы 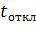 вводят коэффициент 0,5 и за время пуска
вводят коэффициент 0,5 и за время пуска 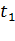 и торможения
и торможения 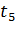 коэффициент 0,75. В этом случае формула для эквивалентного тока принимает следующий вид:
коэффициент 0,75. В этом случае формула для эквивалентного тока принимает следующий вид:
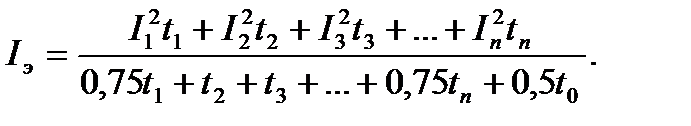 (7.47 )
(7.47 )
Если при выборе мощности электродвигателя приходится пользоваться графиками моментов или мощностей, то определяют по аналогичным формулам эквивалентные моменты или мощность
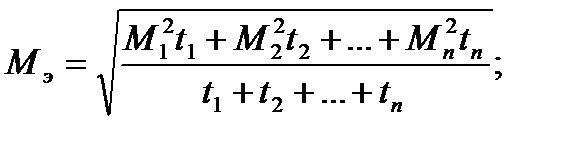 (7.48 )
(7.48 )
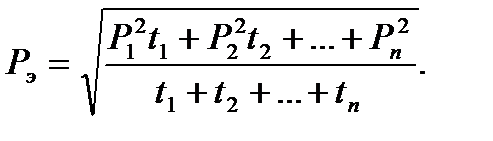 (7.49 )
(7.49 )
Методом эквивалентного тока нельзя пользоваться в случаях, когда существенно изменяется активное сопротивление обмоток электродвигателя в тех или иных режимах (асинхронные электродвигатели с глубоким пазом и двойной клеткой в роторе). В этом случае
пользуются методом средних потерь.
Методом эквивалентного момента дополнительно к приведенным ограничениям для метода эквивалентного тока нельзя пользоваться в случае электродвигателей, в которых магнитный поток изменяется при работе (электродвигатели постоянного тока с последовательным и смешанным возбуждением) - он также непригоден для асинхронных электродвигателей с короткозамкнутым ротором при работе с большими скольжениями (пуск, реверс, торможение). Во всех этих случаях нужно непосредственно определять потери мощности в
электродвигателе.
Методом эквивалентной мощности нельзя пользоваться в случаях, указанных для методов эквивалентного тока и момента, а также если значительно изменяются: частота вращения электродвигателя (частые пуски и отключения, регулирование частоты вращения, торможение), КПД и коэффициент мощности на разных участках графика нагрузки.
Таким образом, методы эквивалентной мощности и момента можно применять для электродвигателей постоянного тока с параллельным и независимым возбуждением и асинхронных электродвигателей, работающих в установившемся режиме. Наиболее точные результаты дает метод эквивалентного тока, который достаточно полно учитывает потери в электродвигателе.
7.5. Дополнительные условия проверки мощности двигателя
Электродвигатель, выбранный по допустимому нагреву необходимо проверить по мощности исходя в общем случае из обеспечения им следующих условий: пуска, статической и динамической устойчивости, допустимого нагрева при продолжительном пуске,
допустимой частоты включений.
Чтобы двигатель успешно запустился при возможном снижении напряжения в сети, его мощность должна быть достаточной для выполнения условия:
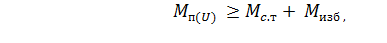 (7.50)
(7.50)
где 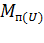 - пусковой момент двигателя с учетом возможного снижения напряжения питания при пуске, Н
- пусковой момент двигателя с учетом возможного снижения напряжения питания при пуске, Н  м;
м; 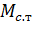 - момент статического сопротивления на валу электродвигателя при трогании с места, Н
- момент статического сопротивления на валу электродвигателя при трогании с места, Н  м;
м; 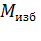 - избыточный момент минимальный, необходимый для
- избыточный момент минимальный, необходимый для
обеспечения пуска, Н  м. Обычно
м. Обычно 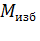 = 0,2
= 0,2 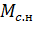
Для асинхронного ЭП (7.50) можно записать:
 =
= 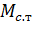 + 0,2
+ 0,2 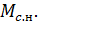 (7.51)
(7.51)
Если обе части выражения (7.51) умножить на номинальную угловую скорость электродвигателя 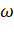 и учесть, что М
и учесть, что М 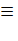 Р , то получим формулу для расчета необходимой мощности асинхронного двигателя из условия обеспечения пуска ЭП:
Р , то получим формулу для расчета необходимой мощности асинхронного двигателя из условия обеспечения пуска ЭП:
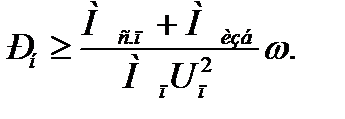 (7.52)
(7.52)
Правила устройства электроустановок (ПУЭ) в общем случае допускают снижение напряжения при пуске асинхронных ЭП до 30% ниже номинального на зажимах пускаемого АД ( 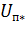 = 0,7) и до 20 % - на зажимах параллельно работающих (
= 0,7) и до 20 % - на зажимах параллельно работающих ( 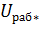 = 0,8). Здесь
= 0,8). Здесь 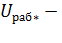 предельно допустимый уровень напряжения на зажимах
предельно допустимый уровень напряжения на зажимах
работающего АД ЭП.
Для обеспечения статической устойчивости мощность ЭП достаточна, если выполняется условие:
 (7.53)
(7.53)
где 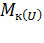 - максимальный (критический) вращающий момент электродвигателя с учетом возможного снижения напряжения питания, Н
- максимальный (критический) вращающий момент электродвигателя с учетом возможного снижения напряжения питания, Н  м;
м; 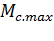 - максимально возможный момент статической нагрузки на валу электродвигателя при работе, Н
- максимально возможный момент статической нагрузки на валу электродвигателя при работе, Н  м.
м.
Применительно к асинхронному ЭП ( 7.53) преобразуют к виду:
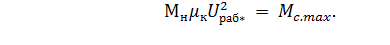 (7.54)
(7.54)
На основании ( 7.54) умножением обеих частей соотношения на 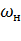 и с учетом, что максимально возможная мощность статической нагрузки на валу электродвигателя при работе
и с учетом, что максимально возможная мощность статической нагрузки на валу электродвигателя при работе 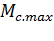 =
= 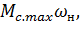 получаем формулу по определению мощности АД из условия
получаем формулу по определению мощности АД из условия
обеспечения статической устойчивости ЭП:
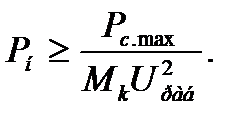 (7.55)
(7.55)
Динамическую устойчивость ЭП при ударной и резко переменной нагрузках оценивают на основании (6.19).
Необходимость в проверке мощности двигателя ЭП по допустимому нагреву при продолжительном пуске возникает при длительности прямого пуска ЭП свыше 10 с. Если в течение пуска пренебречь теплоотдачей электродвигателя, что допустимо, то на основании рассмотрения уравнения теплового баланса электродвигателя (7.5) для данного допущения получим после интегрирования формулу по определению превышения его температуры 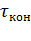 в конце пуска над
в конце пуска над
первоначальной перед пуском в виде:
 = А /(сm )
= А /(сm )  (7.56)
(7.56)
где А - потери энергии в электродвигателе при пуске, Дж; с - средняя удельная теплоемкость электродвигателя, которая может быть принята на уровне 400 Дж/ (кг. град); m- масса электродвигателя, кг.
Нормы допускают кратковременный нагрев изоляции электродвигателей при длительном пуске до температуры 200  С - для изоляции класса нагревостойкости «В» и 225
С - для изоляции класса нагревостойкости «В» и 225  С - для класса «F».
С - для класса «F».
Наряду с кратностями: пускового, максимального и минимального момента, пускового тока ГОСТ 28327 (МЭК 60034-12) регламентирует кратность пусковой мощности кВ  А по отношению к номинальной мощности двигателя кВт
А по отношению к номинальной мощности двигателя кВт
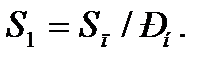 (7.57)
(7.57)
Вследствие этого в отдельных случаях возникает необходимость проверки соблюдения условия (7.57).
Если работа ЭП сопровождается частыми включениями и отключениями, то мощность электродвигателя проверяют по
допустимой частоте включений:
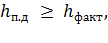
где 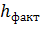 факт - фактическая частота включений двигателя ЭП, ч;
факт - фактическая частота включений двигателя ЭП, ч; 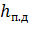 - предельно допустимая частота включений двигателя ЭП,
- предельно допустимая частота включений двигателя ЭП,
исходя из его допустимого нагрева, ч
В предположении, что частичная мощность на валу двигателя при работе близка к номинальной из равенства энергий тепловыделения и теплоотдачи, имеем:
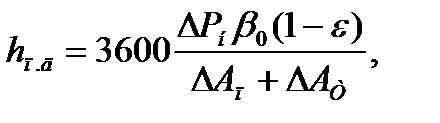 (7.58)
(7.58)
где 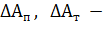 потери энергии соответственно при пуске и электрическом торможении двигателя, Дж;
потери энергии соответственно при пуске и электрическом торможении двигателя, Дж; 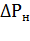 - его номинальные потери мощности, Вт;
- его номинальные потери мощности, Вт; 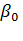 - коэффициент охлаждения для двигателей с самовентиляцией
- коэффициент охлаждения для двигателей с самовентиляцией 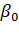 = 0,5;
= 0,5; 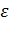 - относительная продолжительность
- относительная продолжительность
включения двигателя ЭП , 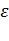 = ПВ/100.
= ПВ/100.
7.6. Подбор редуктора электропривода
Подбор электродвигателей к рабочим машинам – важный этап проектирования электропривода, на котором предусматривают одновременное определение параметров двигателя и механической передачи (в большинстве случаев - редуктора). За счет рационального выбора передаточного числа механической передачи могут быть достигнуты необходимые показатели электропривода. Ими могут быть минимальная продолжительность пуска, наименьшая стоимость, масса, габаритные размеры и потери энергии или максимальный КПД электропривода [22].
Масса, габаритные размеры (и соответственно стоимость) двигателя определяются при заданной мощности его номинальным моментом. Подавляющее количество асинхронных двигателей с высокой номинальной частотой вращения имеют меньшую массу и повышенные значения номинальных коэффициентов полезного действия 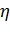 , и коэффициента мощности соs
, и коэффициента мощности соs 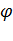 . Поэтому при проектировании электропривода рекомендуется ориентироваться в первую очередь
. Поэтому при проектировании электропривода рекомендуется ориентироваться в первую очередь
на высокоскоростные двигатели.
Однако при использовании высокоскоростных двигателей для обеспечения заданных скоростей движения исполнительных органов рабочих машин и производственных механизмов потребуется применение более тяжелых редукторов с большими значениями передаточного отношения, отличающихся более высокими потерями мощности. Таким образом, задача совместного выбора двигателя и редуктора имеет оптимизационный характер и должна решаться c использованием определенных критериев оптимизации: срока окупаемости, минимума потерь мощности (энергии), минимума стоимости электропривода, максимального быстродействия. Двигатель и редуктор выбирают с учетом параметров напряжения питающей сети, способа монтажа на рабочей машине и условий окружающей среды.
Суммарный приведенный момент инерции электропривода определяется как моментом инерции ротора (якоря) двигателя, так и инерцией элементов механической передачи и исполни тельного органа рабочей машины. Таким образом, за счет выбор передаточного числа (радиуса приведения) механической передачи, с помощью которого осуществляется приведение к валу двигателя масс и моментов инерции элементов механической передачи и исполнительного органа, могут быть оптимизированы определенные показатели работы
электропривода.
Одна из типовых задач такого рода связана с обеспечением минимальной продолжительности пуска или торможения двигателя, т. е. максимального быстродействия электропривода. Этого достигают за счет оптимизации передаточного числа редуктора, которому будут соответствовать минимальный запас кинетической энергии и минимальные потери энергии в переходных процессах.
Если допустить, что моменты двигателя и нагрузки в переходных процессах постоянны, то, относя потери в механической передаче к моменту нагрузки и используя основное уравнение движения, можно для продолжительности переходного процесса 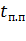 записать
записать
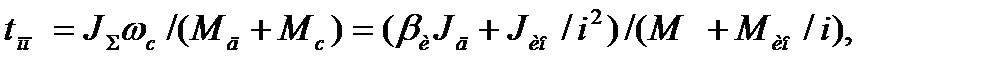 (7.59)
(7.59)
где 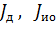 - соответственно моменты инерции двигателя и исполнительного органа;
- соответственно моменты инерции двигателя и исполнительного органа; 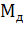 ,
, 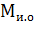 ,
, 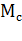 - соответственно моменты двигателя, исполнительного органа и нагрузки на валу двигателя;
- соответственно моменты двигателя, исполнительного органа и нагрузки на валу двигателя; 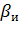 - коэффициент, учитывающий момент инерции элементов редуктора;
- коэффициент, учитывающий момент инерции элементов редуктора;
i - передаточное число редуктора (знак «—» соответствует пуску двигателя, знак «+» - его торможению).
Заменяя в формуле (7.59) передаточное число редуктора отношением частот вращения двигателя и исполнительного органа
( i = 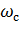 /
/ 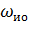 ) . После преобразований получаем
) . После преобразований получаем
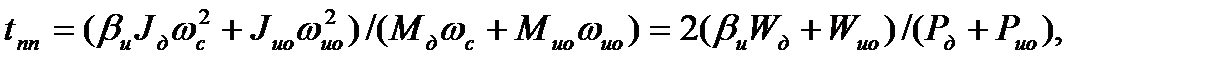 (7.60)
(7.60)
где 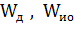 - соответственно запасы кинетической энергии двигателя и исполнительного органа при частоте вращения
- соответственно запасы кинетической энергии двигателя и исполнительного органа при частоте вращения
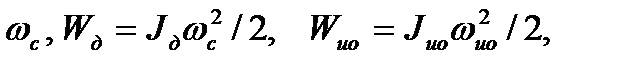
где 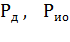 - соответственно мощности двигателя и
- соответственно мощности двигателя и
исполнительного органа.
Из формулы ( 7.60) следует, что минимальной продолжительности переходного процесса соответствуют минимальный запас кинетической энергии в электроприводе и исполнительном органе рабочей машины и минимальные потери энергии в динамических режимах.
Найдем оптимальное передаточное число редуктора для случая пуска двигателя (знак «—» в формулах), при котором время пуска и потери энергии будут минимальными. Для этого находим производную и приравниваем ее к нулю. После преобразований получаем
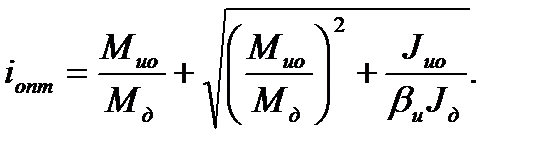 (7.61)
(7.61)
Cледует иметь ввиду, что определенное оптимальное передаточное число, кроме обеспечения минимальных времени и потерь энергии в переходных процессах, должно обеспечить также и необходимую рабочую частоту вращения исполнительного органа рабочей машины.








