Переходные процессы в электроприводах
6.1. Общие сведения
Переходным процессом электропривода называют режим работы при переходе от одного установившегося состояния привода к другому, когда изменяются частота вращения, момент, и ток. Причинами возникновения переходных процессов в электроприводах являются либо изменение нагрузки, связанное с производственным процессом, либо внешнее воздействие на электропривод при управлении им, т. е. пуск, торможение, изменение направления вращения и т.п. Без переходных процессов не совершается работа ни одного электропривода. Даже в простейших нерегулируемых приводах требуется осуществлять пуск, остановку, реверсирование, которые являются наиболее характерными переходными процессами. Пуск и торможение могут быть основными рабочими состояниями, например в электроприводе строгального станка, насоса безбашенной
водокачки и т.п.
Переходные процессы в электроприводах могут возникнуть также в результате аварий или нарушения нормальных условий электроснабжения (например, изменение напряжения или частоты сети, несимметрия напряжения и т.п.).
Изучение переходных процессов электропривода имеет большое практическое значение. Правильный выбор мощности электродвигателей, правильный подбор аппаратов и расчет схем управления, уменьшение расхода энергии при пуске и торможении основаны на знании переходных режимов электроприводов.
Лишь для ограниченного числа исполнительных механизмов можно проектировать электроприводы без учета характера протекания переходных процессов. К ним относятся некоторые редко пускаемые и длительно работающие механизмы с простейшими пусковыми устройствами. Для большинства же рабочих машин характер протекания переходных процессов должен учитываться, так как он оказывает существенное влияние на работу привода.
Для увеличения производительности механизма необходимо не только выбрать оптимальное значение номинальной частоты вращения, но и стремиться к сокращению длительности переходных режимов привода.
Изучение переходных процессов и влияния на них различных электрических и механических параметров, например напряжения, сопротивления, индуктивности, махового момента и т. п., необходимо также для правильного выбора способов управления и расчета схем управления [16].
Значение расхода энергии в периоды пуска и торможения имеет особенно существенное значение для часто пускаемых приводов. Поэтому при расчете переходных режимов следует выбирать экономически целесообразные параметры привода и пытаться уменьшить расход энергии при пусковых и тормозных процессах. Переходные процессы в электроприводе характеризуются переходными механическими, электромагнитными и тепловыми процессами, действующими одновременно и взаимно связанными между собой.
При быстро протекающих процессах изменение теплового состояния электропривода в большинстве случаев не оказывает существенного влияния на другие виды переходных процессов. Поэтому в дальнейшем при изучении переходных процессов в электроприводах изменение теплового состояния двигателя не учитывают.
Внешней причиной, или возмущающим воздействием, вызывающим переходный процесс в электроприводе, могут быть резкие изменения питающего напряжения, механической нагрузки на валу, сопротивления в цепях двигателя.
Электрическая реакция привода на возмущающее воздействие, быстрота и характер переходного процесса зависят от инерционности энергетического машинного устройства.
Запас кинетической энергии в механических звеньях устройства и электромагнитной энергии в элементах его электрических целей не может изменяться мгновенно, поэтому переходные процессы требуют определенного времени,
Когда изменение кинетической энергии в одних элементах вызывает изменение электромагнитной энергии в других, может наступить периодическое преобразование одного вида энергии в другой и характер переходного процесса будет колебательный.
Переходные процессы в электроприводах в общем случае, если учитывать все инерционности, представляют сложное явление. Электромагнитные переходные процессы учитывают при расчете приводов с двигателями постоянного тока большой мощности.
В электроприводах с асинхронными двигателями электромагнитные переходные процессы, связанные с электромагнитной инерционностью, быстротечны и в практических расчетах их влиянием можно пренебречь.
В зависимости от того, какой вид инерции учитывают, переходные процессы электропривода условно делят на механические, т.е. такие, при рассмотрении которых принимают во внимание влияние только механической инерции, и электромеханические, где учитывают влияние не только механической, но и электромагнитной инерции.
6. 2. Механические переходные процессы
Расчеты механических переходных процессов выполняют на
основе уравнения движения электропривода:
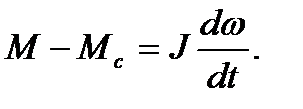 (6.1)
(6.1)
Чтобы определить продолжительность переходного процесса,
разделим переменные
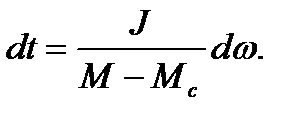 (6.2)
(6.2)
Проинтегрировав обе части равенства (6.2), получим, что
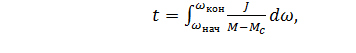 (6.3)
(6.3)
где 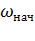 ,
, 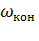 - начальное и конечное значения угловой скорости.
- начальное и конечное значения угловой скорости.
В приближенных расчетах динамический момент (М - 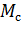 ) и момент инерции считают постоянными величинами, тогда
) и момент инерции считают постоянными величинами, тогда
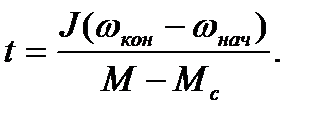 (6.4)
(6.4)
При разгоне из неподвижного состояния, когда 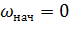 ,
, 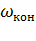 =
= 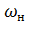 продолжительность разгона ( пуска)
продолжительность разгона ( пуска)
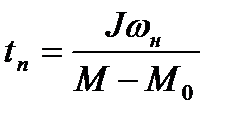 (6.5)
(6.5)
Если осуществляется полная остановка от номинальной частоты вращения, то продолжительность торможения
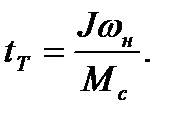 (6.6)
(6.6)
При искусственном торможении
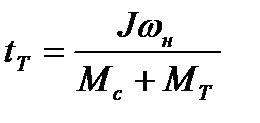 , (6.7)
, (6.7)
где 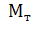 - дополнительный тормозной момент.
- дополнительный тормозной момент.
В тех случаях, когда из-за сложного характера изменения вращающего или статического момента динамический момент нельзя считать постоянным, пользуются графоаналитическим методом определения продолжительности пуска [14]. Построив механические характеристики двигателя 1 (рис.6.1) и рабочей машины 2, строят кривую изменения динамического момента 3.
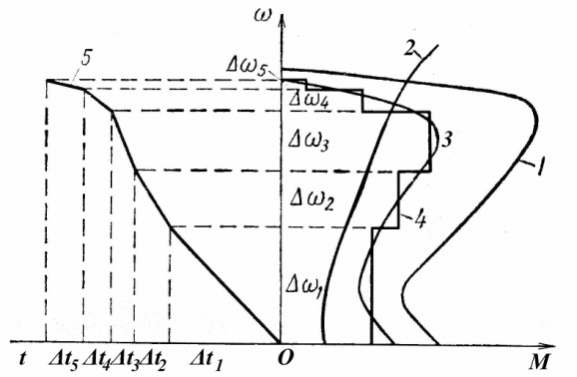
Рис.6.1. Построение графика изменения частоты вращения электро
привода при пуске.
Кривую динамического момента заменяют ломаной ступенчатой линией 4. В пределах каждой ступени динамический момент принимают постоянным, равным среднему значению его на этом участке.
Для каждого участка время разгона
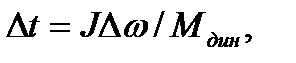 (6.8)
(6.8)
где 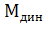 - средний динамический момент на участке.
- средний динамический момент на участке.
Определив продолжительность разгона на участках, сложением можно найти полную продолжительность пуска и построить график изменения частоты вращения электропривода при пуске 5.
Для двигателей, имеющих линейную зависимость момента от частоты вращения в течение переходного процесса и постоянный момент сопротивления, формулы для расчетов можно получить из следующей системы уравнений:
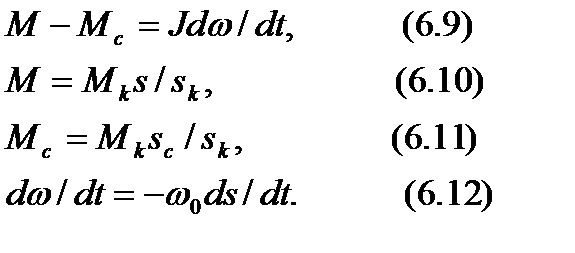
Подставляя в уравнение (6.9) значения из формул (6.10), (6.11), (6.12), получим
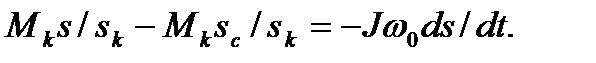 (6.13)
(6.13)
Разделив на М/s все члены последнего уравнения, будем иметь
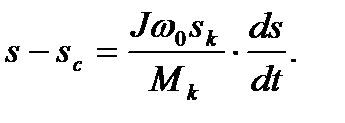 (6.14)
(6.14)
Величину J 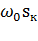 /
/ 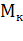 выражаемую в секундах, называют электромеханической постоянной времени переходных процессов.
выражаемую в секундах, называют электромеханической постоянной времени переходных процессов.
Обозначив постоянную времени 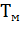 , уравнение (6.14) запишем в виде:
, уравнение (6.14) запишем в виде:
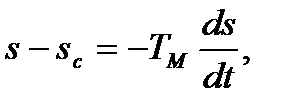 (6.15)
(6.15)
где 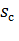 - скольжение двигателя, соответствующее моменту
- скольжение двигателя, соответствующее моменту
сопротивления 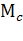 .
.
Поскольку моменты прямо пропорциональны скольжению, последнее уравнение можно записать в виде:
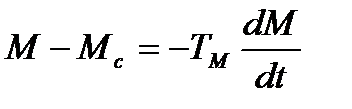 (6.16)
(6.16)
отсюда
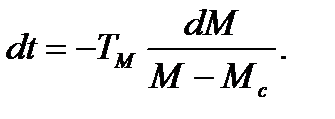 (6.17)
(6.17)
Проинтегрировав обе части последнего равенства в пределах изменения момента от 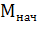 до
до 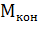 , получим уравнение для определения продолжительности переходного процесса:
, получим уравнение для определения продолжительности переходного процесса:
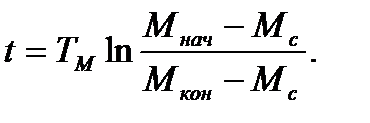 (6.18)
(6.18)
Переходный процесс считают закончившимся, если конечное скольжение или момент отличается от установившегося значения на 2. . . 5%.
Из расчетов по формуле (6.18) следует, что переходный процесс при
таком условии заканчивается за время, равное (3...4) 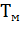 .
.
6.3. Переходные процессы при резкопеременной нагрузке
Нагрузка некоторых машин, например дробилок, прессов, молотилок, представляет собой чередующиеся периоды кратковременного резкого повышения и снижения нагрузки. Эти машины конструируют таким образом, чтобы большие, в течение долей секунды действующие сопротивления преодолевались в основном инерционными силами. При этом нагрузочная диаграмма двигателя существенно отличается от нагрузочной диаграммы рабочей машины (рис.6.2). При большой нагрузке момент двигателя меньше статического, а при малой больше. Среднее значение момента двигателя равно среднему значению статического момента. Выравнивание момента двигателя тем больше, чем больше момент инерции энергетического машинного устройства, поэтому при наличии резкопеременной, которую также называют ударной, нагрузке, привод снабжают маховиком или делают массивными движущие рабочие органы.
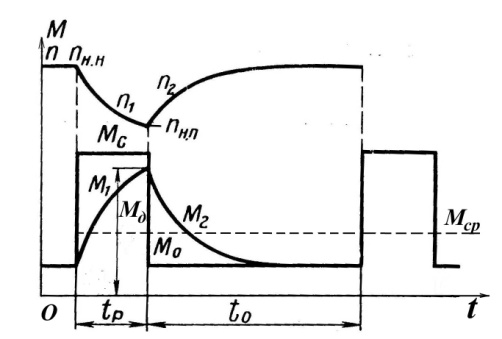
Рис. 6.2. Изменение момента электродвигателя при резкопеременной нагрузке рабочей машины: 1- нагрузочная диаграмма двигателя; 2 – нагрузочная диаграмма рабочей машины.
Необходимый приведенный момент инерции можно определить, вычислив предварительно электромеханическую постоянную времени переходных процессов
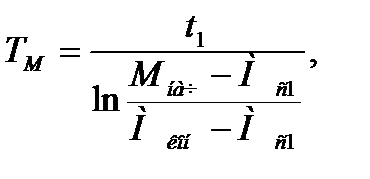 (6.19)
(6.19)
где 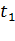 - продолжительность действия большой нагрузки
- продолжительность действия большой нагрузки 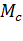 .
.
В то же время,
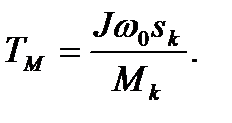 (6.20)
(6.20)
Из уравнений (6.19), ( 6.20)
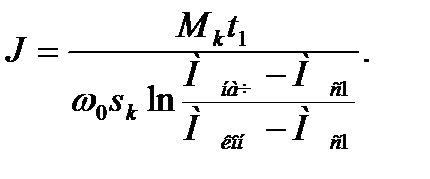 (6.21)
(6.21)
Если собственный приведенный момент инерции энергетического машинного устройства 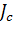 оказывается меньше вычисленного, то устанавливают маховик с моментом инерции
оказывается меньше вычисленного, то устанавливают маховик с моментом инерции 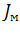 , принимая
, принимая 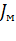 = J -
= J - 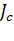 .
.
В приводах машин с резкопеременной нагрузкой применяют двигатели, у которых большое скольжение 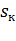 , так как это позволяет
, так как это позволяет
уменьшить 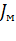 .
.
Поскольку
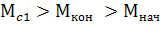 ,
, 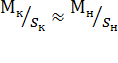 ,
,
то уравнение для определения приведенного момента инерции можно записать в таком виде:
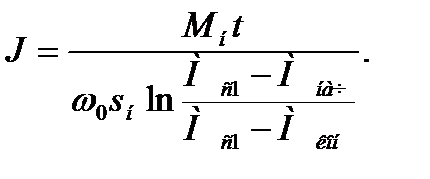 (6.22)
(6.22)
Значения 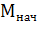 и
и 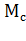 берут из графика нагрузки (рис. 6.2). Значение момента электродвигателя к концу действия большой нагрузки принимают равной 0,75
берут из графика нагрузки (рис. 6.2). Значение момента электродвигателя к концу действия большой нагрузки принимают равной 0,75 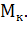
Уравнение для вычисления момента двигателя при ударной нагрузке можно получить из выражения (6.20), определяя из него 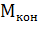 . Алгебраическими преобразованиями и потенцированием логарифмической функции получают выражение:
. Алгебраическими преобразованиями и потенцированием логарифмической функции получают выражение:
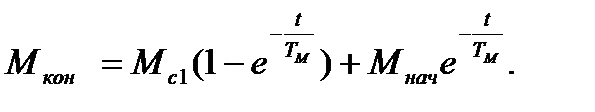 (6.23)
(6.23)
Момент электродвигателя изменяется по экспоненциальным кривым, как показано на рис. 6.2.
Для определения момента двигателя на втором участке в формулу (6.23) подставляют соответствующие значения 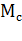 и
и 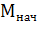 , а именно
, а именно
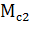 ,
, 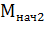 =
= 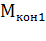 .
.
6.4. Энергопотребление при переходных процессах
При любом переходном процессе затрачивается определенное количество энергии [2]. Эту энергию можно представить в виде двух составляющих: полезной, связанной с выполнением электродвигателем определенной механической работы, и потерь энергии.
Полезная составляющая определяется изменением произведения момента двигателя на его угловую скорость. При этом в пусковых режимах, связанных с увеличением частоты вращения двигателя, энергия из сети расходуется на увеличение кинетической энергии движущихся частей электропривода, а в тормозных, наоборот, кинетическая энергия движущихся частей электропривода возвращается в сеть (при рекуперативном торможении) или выделяется в виде потерь (при динамическом торможении или торможении противовключением). Полезная составляющая энергии определяется технологическим процессом и в пусковых режимах повлиять на нее не представляется возможным, а в тормозных режимах она может быть возвращена в сеть за счет рекуперативного торможения (разумеется, за вычетом потерь).
Потери энергии принято делить на постоянные и переменные. Под постоянными подразумеваются потери энергии, не зависящие от нагрузки двигателя. К ним относятся потери в стали магнитопровода двигателя, механические потери от трения в подшипниках и вентиляционные потери. Постоянные потери не остаются неизменными и зависят от скорости двигателя, амплитуды и частоты питающего его напряжения и т. д. Но так как эти потери изменяются в ограниченных пределах и составляют незначительную часть общих потерь, то они принимаются неизменными и равными постоянным потерям при
номинальном режиме работы двигателя .
С точки зрения оптимизации энергопотребления наибольший интерес представляют переменные потери электропривода, которые складываются из мощности потерь в меди статора и ротора двигателя:
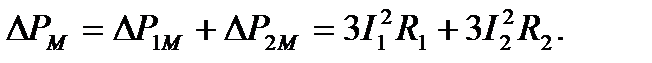 (6.24)
(6.24)
Браславский, И.Я. рекомендует использовать Г- образную схему замещения (см. рис.4.1) для анализа потерь в меди статора [2].
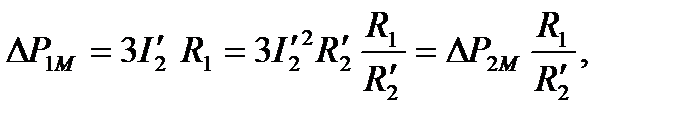 (6.25)
(6.25)
а суммарные потери в меди
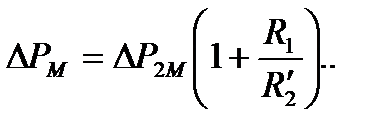 (6.26)
(6.26)
Тогда потери энергии в течение переходного процесса 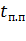 ,
,
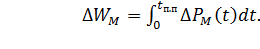 (6.27)
(6.27)
Использование формулы (6.27) для оценки потерь энергии за время переходного процесса затруднительно, так как для этого необходимо знать законы изменения токов двигателя 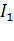 и
и 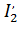 в переходном процессе, а также располагать данными об изменении сопротивлений.
в переходном процессе, а также располагать данными об изменении сопротивлений.
Удобные расчетные соотношения можно получить при использовании механических переменных и параметров. Используя известное соотношение для переменных потерь в роторе (потерь скольжения)
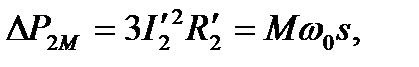 (6.28)
(6.28)
найдем энергию потерь в роторе за время переходного процесса:
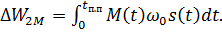 (6.29 )
(6.29 )
Рассмотрим потери энергии при работе электропривода без нагрузки
( 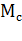 = 0).
= 0).
Из уравнения механического движения электропривода при М = 0 получим
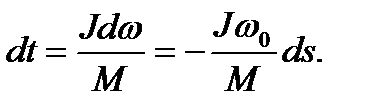
Подставив полученное значение dt в формулу (6.29) и заменив
пределы интегрирования, получим
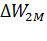 =
= 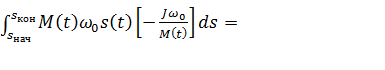 (6.30)
(6.30)
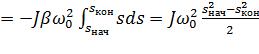 .
.
Выражение (6.30) более удобно для определения потерь энергии, так как для расчетов необходимо знать лишь параметры J и 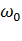 , начальное и конечное значения скольжения s.
, начальное и конечное значения скольжения s.
Для примера найдем потери энергии в роторе асинхронного двигателя при его пуске, торможении и реверсе вхолостую.
При пуске двигателя 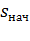 = 1 ,
= 1 , 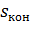 = 0, поэтому
= 0, поэтому
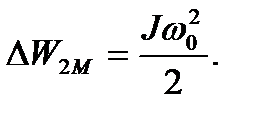 (6.31)
(6.31)
Потери энергии в роторе в соответствии с (6.31), численно равны кинетической энергии, которая будет запасена к концу пуска в движущихся частях электропривода.
Так как при динамическом торможении 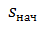 = 1 ,
= 1 , 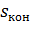 = 0, то потери энергии также определяются выражением (6.31). При этом весь запас кинетической энергии электропривода превращается в потери, выделяемые в виде теплоты.
= 0, то потери энергии также определяются выражением (6.31). При этом весь запас кинетической энергии электропривода превращается в потери, выделяемые в виде теплоты.
При торможении противовключением 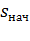 = 2,
= 2, 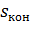 = 1, а потери энергии
= 1, а потери энергии 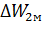 = 3J
= 3J 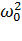 /2, т.е. в З раза превышают потери при пуске и динамическом торможении и численно равны тройному запасу кинетической энергии.
/2, т.е. в З раза превышают потери при пуске и динамическом торможении и численно равны тройному запасу кинетической энергии.
При реверсе 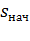 = 2,
= 2, 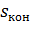 = 0, а потери энергии
= 0, а потери энергии 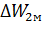 = 4J
= 4J 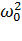 /2,
/2,
т. е. они равны сумме потерь при торможении противовключением
и пуске.
Таким образом, потери энергии в роторе 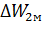 , за время переходного процесса при
, за время переходного процесса при 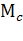 = 0 не зависят от времени, а определяются только начальным
= 0 не зависят от времени, а определяются только начальным 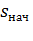 и конечным
и конечным 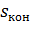 значениями скольжения и суммарным моментом инерции электропривода J. Потери энергии зависят не только от значения изменения скольжения (
значениями скольжения и суммарным моментом инерции электропривода J. Потери энергии зависят не только от значения изменения скольжения ( 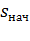 –
– 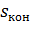 ), но и от абсолютных значений скольжения. Найдем потери при изменении скольжения на 0,5 при разных значениях
), но и от абсолютных значений скольжения. Найдем потери при изменении скольжения на 0,5 при разных значениях 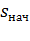 . Так, при
. Так, при 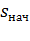 = 1 и
= 1 и
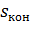 = 0
= 0 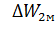 = 0,75J
= 0,75J 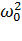 /2, а при
/2, а при 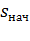 = 0,5 и
= 0,5 и 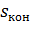 = 0
= 0 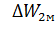 = 0,25J /2, т.е. потери энергии отличаются в З раза.
= 0,25J /2, т.е. потери энергии отличаются в З раза.
Представление о зависимости энергии потерь в роторе от 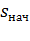 и
и 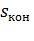 дают графики зависимости относительных потерь в меди ротора АД от
дают графики зависимости относительных потерь в меди ротора АД от 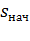 и
и 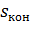 , приведенные на рис.6.3 (относительные потери энергии даны в долях от значения J
, приведенные на рис.6.3 (относительные потери энергии даны в долях от значения J 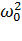 /2, принятой за базовую
/2, принятой за базовую 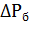 ). На рис.6.3 видно, что при одном и том же изменении скольжения s потери будут тем меньше, чем ближе к нулю значения
). На рис.6.3 видно, что при одном и том же изменении скольжения s потери будут тем меньше, чем ближе к нулю значения 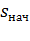 и
и 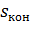 , т.е. переходные процессы вблизи угловой скорости холостого хода связаны с меньшими потерями.
, т.е. переходные процессы вблизи угловой скорости холостого хода связаны с меньшими потерями.
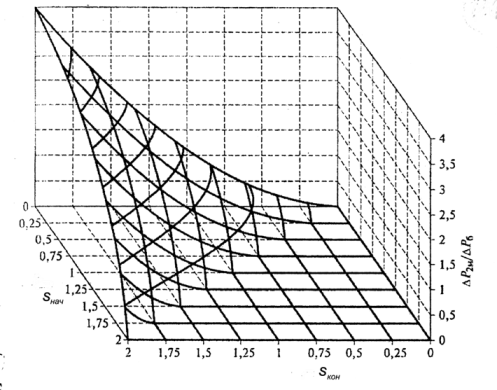
Рис.6.3.Зависимость относительных потерь в роторе
асинхронного двигателя от значений скольжения.
Кроме того, одинаковые изменения скорости в разных направлениях приводят к разным потерям.
Из выражения (6.30) следует, что потери энергии в роторной цепи двигателя не зависят от времени переходного процесса. Это означает, что они не зависят и от формы механических характеристик электропривода. Так, для любой из механических характеристик асинхронного электропривода, примеры которых приведены на рис. 6.4, потери энергии в роторе при одинаковых изменениях скорости будут равными, не зависящими от значения сопротивления роторной цепи.
Это обстоятельство физически объясняется тем, что механическим характеристикам, для которых при данной скорости моменты больше, соответствуют большие потери, но меньшая продолжительность
переходных процессов.
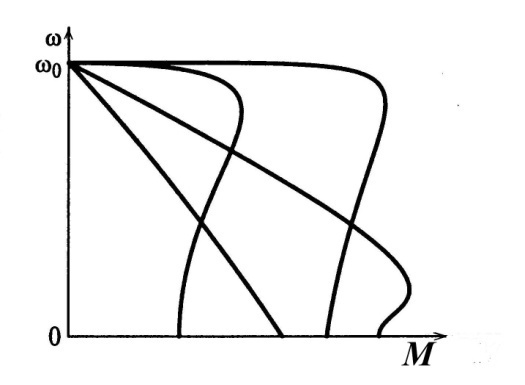
Рис. 6.4.Примеры механических характеристик асинхронных
двигателей, которым соответствуют одинаковые потери в ро торе
при пуске М = 0.
Для определения суммарных потерь энергии в меди АД необходимо найти потери в меди статора. Очевидно, что 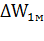 =
= 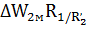
т.е. эти потери зависят от сопротивлений резисторов в статорной и роторной цепей. Чем меньше сопротивление статорной цепи и больше роторной, тем меньше потери в статоре асинхронного двигателя. Уменьшение потерь в статоре с ростом сопротивления ротора
объясняется уменьшением пускового тока [2].
В двигателях общего назначения с короткозамкнутым ротором обычно 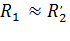 , т.е. в этом случае п отери в меди статора и ротора примерно одинаковы.
, т.е. в этом случае п отери в меди статора и ротора примерно одинаковы.
За счет применения двигателей со специальной конструкцией короткозамкнутого ротора, имеющего повышенное сопротивление, потери в статоре могут быть уменьшены. Например, это двигатели со сплошным стальным ротором и двигатели с повышенным номинальным скольжением краново-металлургической серии. Двигатели, имеющие ротор с глубокими пазами или с двойной «беличьей клеткой», также обладают повышенным сопротивлением ротора, зависящим от скольжения, что приводит к уменьшению переменных потерь в статоре.
Полные потери в меди АД
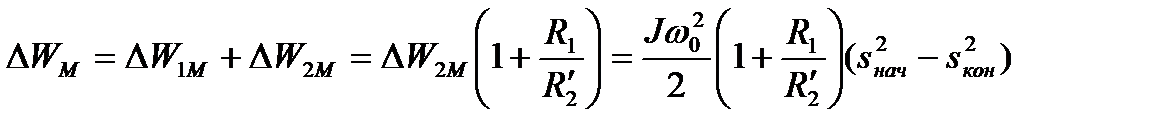 , (6.32)
, (6.32)
Для оценки суммарных потерь энергии в переходном процессе должны быть учтены рассмотренные выше постоянные потери энергии, которые будут зависеть от длительности переходного процесса, однако их учет даст более точное представление о потерях энергии только при чрезвычайно затянутых переходных процессах.
Потери энергии при работе электропривода с нагрузкой ( 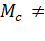 0).
0).
Для определения потерь энергии в меди ротора можно использовать формулу (6.29). При этом необходимо знать, как изменяются момент М(t) и скольжение s(t) двигателя в переходном процессе, а также
закон изменения М(t).
На основе уравнения движения электропривода
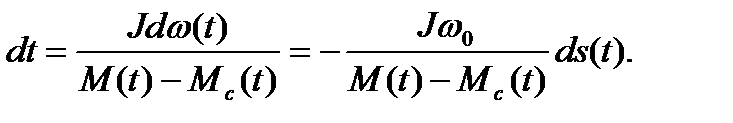 (6.33)
(6.33)
Подставив полученное значение dt в формулу (6.29) и заменив пределы интегрирования, найдем
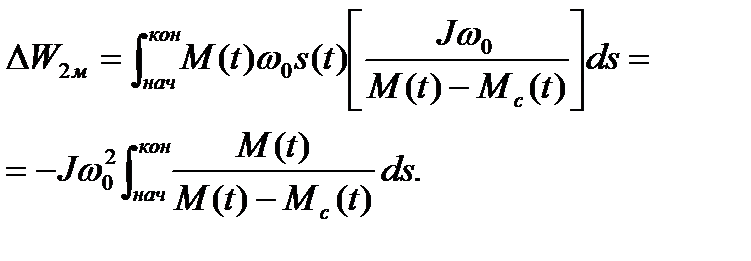 (6.34)
(6.34)
Для оценочных расчетов можно принять, что момент двигателя и статический момент в переходном процессе не изменяются и равны некоторым средним значениям 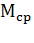 и
и 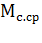 . Тогда
. Тогда
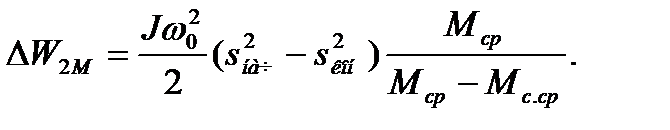 (6.35)
(6.35)
Для иллюстрации зависимости потерь в меди ротора от нагрузки двигателя на рис.6.5 приведены графики относительных потерь (в долях от J 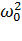 /2) при пуске и динамическом торможении с постоянными моментом М и моментом нагрузки
/2) при пуске и динамическом торможении с постоянными моментом М и моментом нагрузки 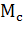 , которые выражены в относительных единицах (за базовый момент принят
, которые выражены в относительных единицах (за базовый момент принят 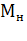 ).
).
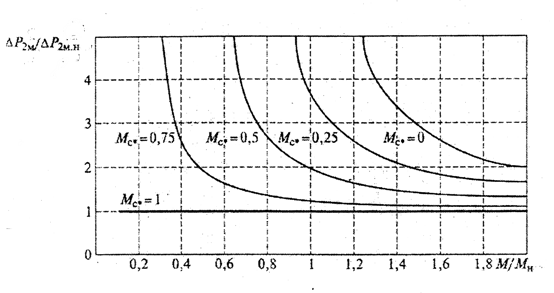
Рис.6.5. Зависимость относительных потерь в меди ротора
асинхронного двигателя при разных моментах нагрузки.
Из рисунка видно, зависимость потерь в меди ротора от нагрузки имеет вид гиперболы, кривизна которой уменьшается с уменьшением нагрузки. В соответствии с формулой (6.35) и приведенными на рис.6.5,  графиками потери энергии в роторе АД при работе под нагрузкой увеличиваются в пусковых режимах и уменьшаются -----------------------
графиками потери энергии в роторе АД при работе под нагрузкой увеличиваются в пусковых режимах и уменьшаются -----------------------
1 Графики рис.6.3…6.5 имеются у Браславского, И.Я.[2].
в тормозных. Последнее обстоятельство связано с тем, что при торможении часть запасенной кинетической энергии расходуется на преодоление момента нагрузки, поэтому в двигателе выделяется в виде потерь только оставшаяся ее часть.
Потери при торможении могут быть снижены практически до нуля, если 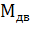 = 0. Это так называемый режим самоторможения - «выбега» двигателя, когда торможение осуществляется за счет
= 0. Это так называемый режим самоторможения - «выбега» двигателя, когда торможение осуществляется за счет 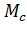 . Вместе с тем в пусковых режимах потери многократно возрастают, если
. Вместе с тем в пусковых режимах потери многократно возрастают, если
момент двигателя близок к моменту нагрузки.
Это связано с тем, что в данном случае динамический момент и соответственно ускорение двигателя очень малы и процесс пуска затягивается. Поэтому можно сделать вывод о том, что если это допустимо по технологии, то целесообразно предусматривать пуск двигателя вхолостую, а торможение под нагрузкой.
Для расчета потерь в меди ротора в переходных процессах под нагрузкой можно получить еще одну зависимость, если учесть, что по сравнению с переходными процессами при пуске АД вхолостую они будут отличаться временной продолжительностью. При М = соnst продолжительность пуска и торможения вхолостую 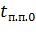 = J
= J 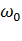 /M.
/M.
Продолжительность пуска и торможения под нагрузкой (снижением
частоты вращения в установившемся режиме пренебрегаем)
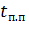 = J
= J 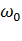 /(М
/(М 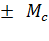 ),
),
поэтому потери энергии в переходном процессе можно рассчитать по
формуле
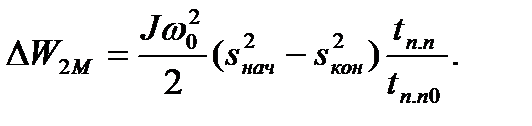 (6.36)
(6.36)
Таким образом, в неуправляемых переходных процессах, когда угловая скорость задается скачком, потери энергии за время переходного процесса пропорциональны суммарному моменту инерции электропривода J, квадрату угловой скорости идеального холостого хода 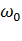 и зависят от диапазона изменения скольжений и нагрузки электропривода.
и зависят от диапазона изменения скольжений и нагрузки электропривода.
Анализ формул (6.30) и (6.35 ) приводит к двум основным способам снижения потерь энергии в переходных режимах:
1) уменьшение суммарного момента инерции электропривода J;
2) регулирование в переходных процессах угловой скорости идеального холостого хода, т.е. использование управляемых переходных
процессов. Особенно эффективны эти способы для электроприводов с частыми пусками и торможениями.
Момент инерции электропривода уменьшается в случаях:
1.Применения малоинерционных двигателей.
2. Рационального конструирования механической передачи (выбор оптимальных передаточного числа редуктора , массогабаритных показателей механической передачи и т. д.).
3. Замены одного двигателя двумя и более с сохранением суммарной мощности.
Регулирование угловой скорости идеального холостого хода осуществляется следующими способами: изменением числа пар полюсов в многоскоростных АД или изменением частоты питающего
напряжения в системе ППЧ - АД.
В процессе пуска двухскоростного АД (рис.6.6) [6] путем переключения обмоток статора при пуске можно в 2 раза увеличить число пар полюсов, т. е. в 2 раза уменьшить угловую скорость идеального холостого хода, снизив ее до 0,5 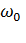 . При этом потери за время пуска вхолостую до угловой скорости 0,5
. При этом потери за время пуска вхолостую до угловой скорости 0,5 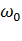 (
( 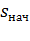 = 1 и
= 1 и 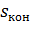 = 0 ) составят
= 0 ) составят
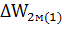 = J
= J 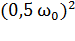 /2 = J
/2 = J 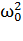 /8.
/8.
На участке пуска от 0,5 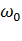 до
до 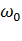 в результате переключения обмоток (полюсов) синхронная угловая скорость увеличивается до
в результате переключения обмоток (полюсов) синхронная угловая скорость увеличивается до 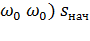 =
= 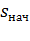 = 0,5;
= 0,5; 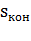 = 0 и потери составят
= 0 и потери составят
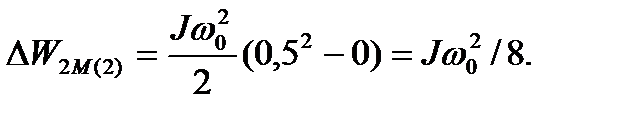 (6.37)
(6.37)
Суммарные потери в меди ротора за время ступенчатого пуска
составят 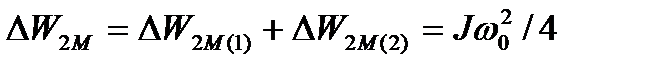 , (6.38)
, (6.38)
что в 2 раза меньше, чем при прямом пуске.
В общем случае, если угловая скорость идеального холостого хода в переходном процессе имеет п одинаковых ступеней регулирования, потери энергии в роторе также уменьшаются в п раз, т. е.
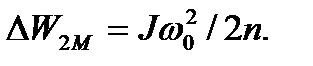 (6.39)
(6.39)
Сокращаются потери в многоскоростном АД и при ступенчатом торможении с высокой частоты вращения. При торможении противовключением в одну ступень двигатель с характеристики 1 переходит на работу по характеристике 3, соответствующей тому же числу пар полюсов двигателя, но при измененном порядке чередования фаз на статоре. Потери энергии в роторе за время торможения до нулевой частоты вращения
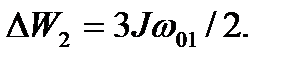 (6.40)
(6.40)
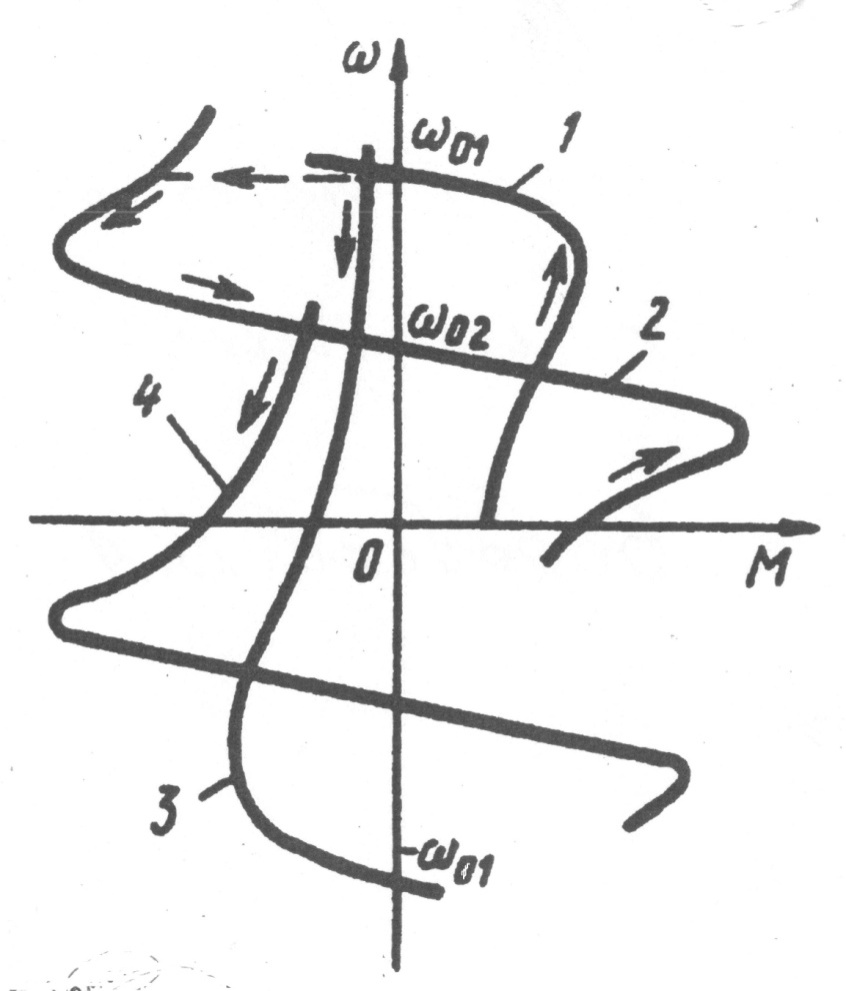
Рис.6.6. Механические характеристики двухскоростного
асинхронного двигателя при пуске и торможении.
При ступенчатом торможении путем изменения числа пар полюсов с 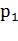 на 2
на 2 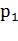 АД сначала переходит на работу по характеристике 2, при которой он тормозится до угловой скорости
АД сначала переходит на работу по характеристике 2, при которой он тормозится до угловой скорости 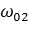 с отдачей энергии
с отдачей энергии
в сеть. Потери на этом этапе ( при 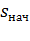 = -1,
= -1, 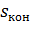 =0)
=0)
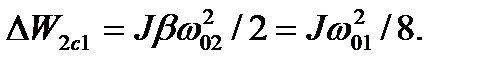 (6.41)
(6.41)
На следующем этапе путем изменения чередования фаз при том же числе пар полюсов осуществляется торможение противовключением (характеристика 4), при котором ( 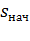 = 2,
= 2, 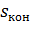 = 1) потери составят
= 1) потери составят
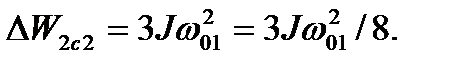 (6.42)
(6.42)
Суммарные потери при ступенчатом торможении
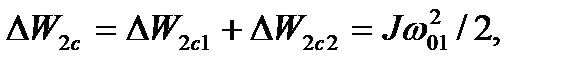 (6.43)
(6.43)
т.е. при ступенчатом торможении потери в три раза меньше, чем при прямом торможении. Пропорционально этому снижаются потери в статоре и суммарные потери в АД.
Можно показать, что и при динамическом торможении в две
ступени потери энергии уменьшатся в 2 раза [12].
Следует иметь в виду, что момент инерции многоскоростного двигателя значительно выше момента инерции односкоростного двигателя с той же мощностью и номинальной частотой вращения, поэтому замена односкоростного двигателя многоскоростным только для уменьшения потерь энергии представляется нецелесообразной. Можно говорить только о сравнении прямого и ступенчатого пуска для одного и того же многоскоростного асинхронного двигателя.
Еще более эффективным путем снижения потерь является непрерывное управление угловой скоростью идеального холостого хода путем изменения частоты питающего АД напряжения в
системе ППЧ - АД.
Представим переходный процесс пуска АД вхолостую при изменении частоты напряжения на статоре так, чтобы сформировать закон изменения скорости идеального холостого хода в виде :
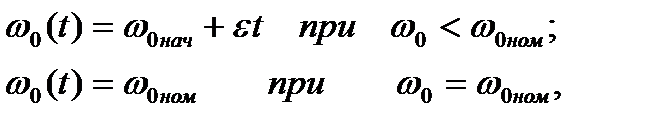 (6.44)
(6.44)
где 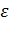 - ускорение электропривода, обеспечивающее заданное время переходного процесса
- ускорение электропривода, обеспечивающее заданное время переходного процесса 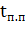 = J
= J 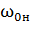 /М при постоянном моменте двигателя М,
/М при постоянном моменте двигателя М, 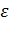 = d
= d 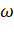 /dt =
/dt = 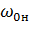 /
/ 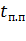 .
.
На рис.6.7 показаны графики переходных характеристик при частотном пуске АД вхолостую.
При постоянном моменте М, выбранном исходя из допустимого ускорения или по перегрузочной способности двигателя или преобразователя, такое управление обеспечивает в меди ротора потери энергии:
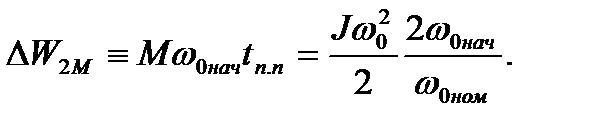 (6.45)
(6.45)
Эти потери по сравнению с прямым пуском снижаются пропорционально 2 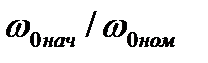
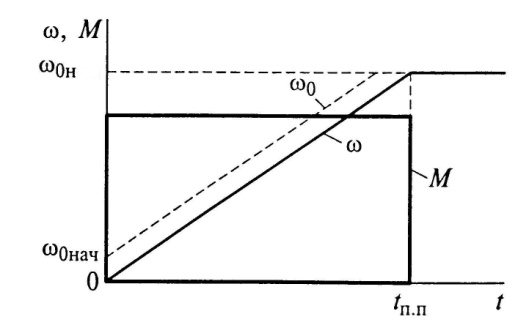
Рис. 6.7. Переходные характеристики при частотном
пуске асинхронного двигателя вхолостую.
В зависимости от мощности и типа двигателя потери могут уменьшиться в 5 - 10 раз.
При определении полных потерь энергии за время переходного процесса асинхронного двигателя необходимо учитывать, что к переменным потерям относятся и потери в меди
статора. С учетом (6.32) потери энергии в меди АД (переменные потери) составят
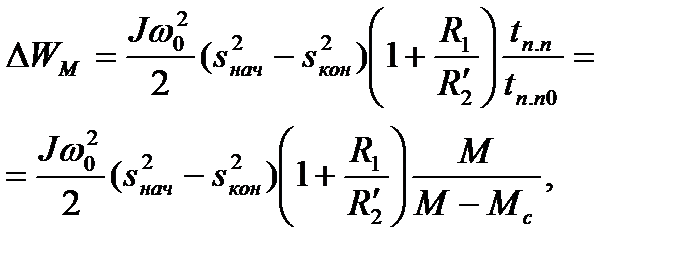 (6.46)
(6.46)
а суммарные потери в двигателе с учетом постоянных потерь составят
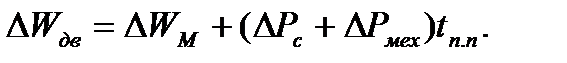 (6.47)
(6.47)
Выражения (6.46) и (6.47) оценочные, так как получены при определенных допущениях. С их помощью можно при проектировании и модернизации асинхронного электропривода выбирать такие технические решения, благодаря которым можно обеспечить минимизацию потерь энергии при переходных режимах работы электропривода.
Глава 7.
Подбор двигателей к рабочим машинам и
тепловые режимы двигателей
7.1. Общие сведенияи тепло
Правильный выбор мощности двигателей во многом определяет первоначальные затраты и стоимость эксплуатационных расходов в электроприводах. Применение двигателя недостаточной мощности может привести к нарушению нормальной работы механизма, к снижению его производительности, возникновению аварий и преждевременному выходу двигателя из строя. В свою очередь использование двигателей завышенной мощности ухудшает экономические показатели установки, ведет к ее удорожанию и большим потерям энергии. В этом случае не только повышается первоначальная стоимость электропривода, но увеличиваются и потери энергии за счет снижения КПД двигателя, а в установках переменного тока, кроме того, ухудшается коэффициент мощности, значение которого непосредственно влияет на непроизводительную загрузку распределительных сетей и генераторов электрических станций, производящих энергию. Весомость вопроса становится понятным, если представить, какое огромное число механизмов приводится электрическими двигателями во всех областях хозяйственной деятельности.
Мощность электродвигателя выбирается, исходя из необходимости обеспечить выполнение заданной работы электропривода, при соблюдении нормального теплового режима и допустимой механической перегрузки двигателя.
Выбор мощности электродвигателей требует также расчета нагрузки привода не только при установившейся работе, но и в периоды переходных режимов. С этой целью обычно строятся так называемые нагрузочные диаграммы, под которыми понимаются зависимости вращающего момента, мощности и тока двигателя от времени, т. е.
М = f(t) ; Р = f(t) и I = f (t) .
В каждом случае двигатель, выбранный в соответствии с заданной нагрузочной диаграммой, должен быть полностью загружен и при этом работать без перегрева сверх допустимых пределов. Аналогичным образом он должен обеспечивать нормальную работу при возможных временных перегрузках и обладать достаточным пусковым моментом для обеспечения требуемой длительности пуска рабочего механизма.
7.2. Нагрев и охлаждение двигателя
В подавляющем числе случаев мощность двигателя выбирают по нагреву, а затем его проверяют по перегрузочной способности, как показано ниже. Нагревание двигателя происходит за счет потерь, возникающих в нем при преобразовании электрической энергии в механическую.
Потери энергии в стали, меди и потери на трение вызывают нагревание различных частей машины; при этом происходит также взаимное нагревание отдельных частей машины. Эти потери могут быть записаны в общем виде одним из следующих равенств:
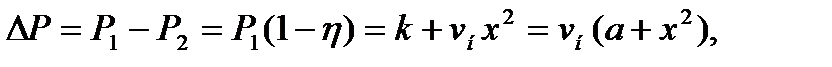 (7.1)
(7.1)
где 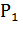 и
и 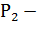 соответственно мощность, подведенная к двигателю, и мощность на его валу;
соответственно мощность, подведенная к двигателю, и мощность на его валу;
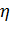 - КПД; k - постоянные потери (в стали, подшипниках и вентиляционные), практически не зависящие от нагрузки;
- КПД; k - постоянные потери (в стали, подшипниках и вентиляционные), практически не зависящие от нагрузки; 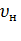 - переменные потери (потери в меди) при номинальной нагрузке; а = k/
- переменные потери (потери в меди) при номинальной нагрузке; а = k/ 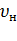 - коэффициент постоянных потерь;
- коэффициент постоянных потерь;
х = 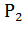 /
/  номинальная мощность двигателя.
номинальная мощность двигателя.
Вследствие выделения теплоты при нагрузке температура двигателя постепенно повышается, и если бы двигатель не отдавал теплоту в окружающую среду, она могла бы достигнуть бесконечно большого значения. Однако рассеивание теплоты поверхностью двигателя в окружающую среду, все увеличивающееся с возрастанием температуры двигателя, ограничивает его нагрев, и повышение температуры по истечении некоторого времени прекращается. Происходит это тогда, когда количество теплоты, отдаваемой двигателем в окружающую среду в единицу времени, становится равным количеству теплоты, выделяемой в двигателе за то же время. Такой тепловой режим, при котором достигается постоянство температуры (установившаяся температура), получается при длительной работе двигателя. Во многих случаях работа прекращается раньше, чем будет достигнута, установившаяся температура, или происходит снижение нагрузки, а следовательно, уменьшение потерь и снижение температуры двигателя.
В соответствии с этим при выборе мощности двигателя по условиям нагревания различают четыре основных стандартных режима работы: S1- продолжительный, S2 - кратковременный, S3 – повторно-кратковременный и S6 – перемежающийся и дополнительные:
S4 - повторно-кратковременный с частыми пусками, S5- повторно-кратковременный с частыми пусками и электрическим торможением, S7 - перемежающийся с частыми реверсами и S8 - перемежающийся с изменением частоты вращения [17]. Условное обозначение режима работы проставляется на паспортном щитке двигателя.
Продолжительный режим работы. В этом режиме рабочий период столь велик, что температура двигателя достигает своего установившегося значения. В качестве примеров здесь могут служить длительно работающие двигатели вентиляторов, насосов, и т. п., где продолжительность работы измеряются часами или даже сутками. Упрощенный график работы для этого режима приведен на рис. 7.1.
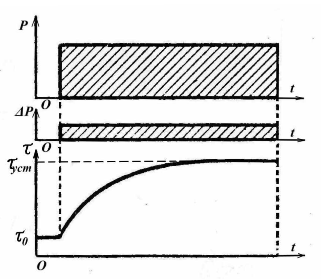
Рис.7.1. Продолжительный режим работы электродвигателя (графики изменения: мощности Р; потерь мощности - 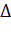 Р; превышения
Р; превышения
температуры -  ).
).
Кратковременный режим работы характерен тем, что в рабочий период температура двигателя не успевает достигнуть установившегося значения, а пауза столь длительна, что температура двигателя снижается до температуры окружающей среды. Для кратковременного нагрузочного режима работы S2 помимо мощности указывают и предельную продолжительность работы с этой мощностью. Электродвигатели режима S2 выпускают на стандартные продолжительности работы10, 30, 60 и 90 мин. Такой режим встречается, например, в приводах задвижек кормодробилок, и др., где пауза в работе значительно превышает длительность рабочего периода. Упрощенный график нагрузки такого режима приведен на рис.7.2 .
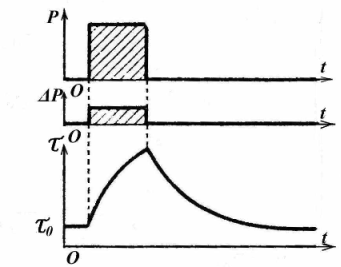
Рис.7.2. Кратковременный режим работы электродвигателя (графики изменения: мощности – Р; потерь мощности – 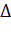 Р;
Р;
превышения температуры -  )
)
Повторно-кратковременный режим работы S З. При этом режиме ни в одном из периодов работы температура двигателя не достигает установившегося значения, а во время паузы двигатель не успевает охладиться до температуры окружающей среды. Типичный пример для подобных приводов - приводы конвейеров, дробилок, центрифуг и др. Упрощенный график нагрузки такого режима показан на рис.7.3.
Повторно-кратковременный режим работы характеризуется коэффициентом относительной продолжительности рабочего периода, под которым понимается отношение продолжительности рабочего периода к продолжительности рабочего цикла (суммарной продолжительности рабочего периода и паузы).
ПВ% = 100 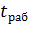 /
/ 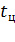 (7.2) где
(7.2) где 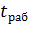 ,
, 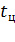 - продолжительности соответственно работы и одного цикла при t ,
- продолжительности соответственно работы и одного цикла при t , 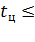 10 мин. ,
10 мин. , 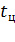 =
= 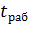 +
+ 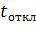 , (
, ( 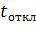 - продолжительность отключения двигателя.
- продолжительность отключения двигателя.
Режимы работы двигателя ЭП повторно-кратковременный с частыми пусками S4 и повторно-кратковременный с частыми пусками и электрическим торможением S5 помимо значений мощности и ПВ еще характеризуются допускаемой частотой включений в час h со стандартными значениями 30, 60, 120 и 240 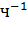 при оговоренном коэффициенте инерции ЭП FJ со стандартными значениями 1,2; 1,6; 2,5 и 4. Стандартные значения ПВ: 15, 25, 40 и 60 %.
при оговоренном коэффициенте инерции ЭП FJ со стандартными значениями 1,2; 1,6; 2,5 и 4. Стандартные значения ПВ: 15, 25, 40 и 60 %.
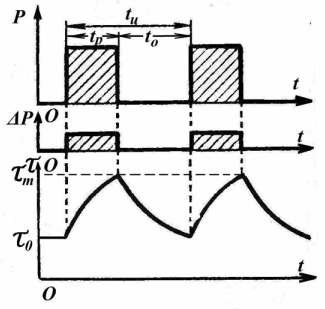
Рис.7.3. Повторно-кратковременный режим работы электродвигателя (графики изменения: мощности – Р; потерь мощности - 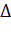 Р;
Р;
превышения температуры -  ).
).
Электродвигатели перемежающегося режима S6 (рис.7.4) наряду с номинальной мощностью характеризуются номинальным значением продолжительности нагрузки (ПН):
ПН% = 100 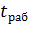 /
/  (7.3)
(7.3)
где 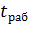 ,
, 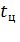 - продолжительности работы, холостого хода и
- продолжительности работы, холостого хода и
одного цикла при t 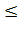 =10 мин.
=10 мин.
Стандартные значения ПН: 15, 25, 40 и 60 %.
Для режима перемежающегося с частыми реверсами S7 дополнительно указывают число реверсов в час (стандартные значения 30, 60, 120 и 240 рев/ч при FJ =1,2; 1,6; 2,5 и 4), а для перемежающегося режима с изменением частоты вращения S8 - продолжительность
работы с разной частотой вращения.
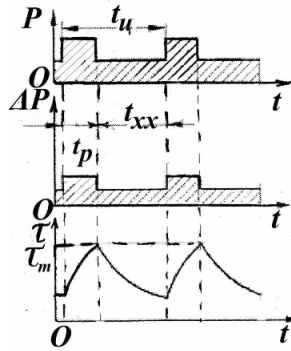
Рис.7.4. Перемежающийся режим работы электродвигателя (графики изменения: мощности – Р; потерь мощности – Р;
превышения температуры -  ).
).
Методы выбора мощности двигателей для каждого из трех основных указанных режимов работы несколько различаются, поскольку условия нагревания машин для них различны. Решение задачи осложняется еще и тем, что графики нагрузки в таком виде, как они представлены на рис. 7.1…7.3, в практических случаях не встречаются.
Обычно механизмы работают при непрерывно изменяющейся нагрузке, как это бывает, например, у дробилок, конвейеров и т. п. На основании общей теории нагрева двигателей удается получить удовлетворительную методику расчета мощности двигателей для различных случаев.
Допустимое нагревание двигателей определяется нагревостойкостью применяемых изоляционных материалов. Более нагревостойкие материалы изоляции позволяют при тех же размерах двигателя увеличивать его мощность. Лучшее использование двигателя может быть достигнуто также за счет применения более совершенной системы его охлаждения.
Все изолирующие материалы, применяемые в электрических машинах, подразделяют на классы нагревостойкости, представленные
в таблице 7.1
Таблица 7.1
Нагревостойкость электроизоляционных материалов
| Класс нагревостойкости | Температура,
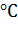
| Характеристика основных групп электроизоляционных материалов и их сочетаний данного класса нагревостойкости |
| 1 | 2 | 3 |
| Y | 90 | Непропитанные и не погруженные в жидкий электроизоляционный материал волокнистые материалы из целлюлозы, хлопка и шелка. |
| A | 105 | Пропитанные или погруженные в жидкий электроизоляционный материал волокнистые материалы из целлюлозы, хлопка или шелка. |
| E | 120 | Некоторые синтетические органические пленки. |
| B | 130 | Материалы на основе слюды (в том числе на органических подложках), асбеста и стекловолокна, применяемые с органическими связывающими и пропитывающими составами. |
| F | 155 | Материалы на основе слюды, асбеста и стекловолокна, применяемые в сочетании с кремнийорганическими связывающими и пропитывающими составами, кремнийорганические эластомеры. |
| H | 180 | Материалы на основе слюды, асбеста и стекловолокна, применяемые в сочетании с кремнийорганическими связывающими и пропитывающими составами. |
| C | Более 180 | Слюда, керамические материалы, стекло, кварц, применяемые без связывающих составов или с неорганическими или элементоорганическими связывающими составами. |
Нагревостойкость - способность электроизоляционного материала выполнять свои функции при воздействии рабочей температуры в течение времени, сравнимого с расчетным сроком нормальной эксплуатации электрооборудования, в котором применяется данный электроизоляционный материал. Указанные в таблице температуры предельно допустимые для электроизоляционных материалов при их длительном использовании (в течение ряда лет) в электрических машинах, трансформаторах и аппаратах, работающих в нормальных эксплуатационных условиях. Класс нагревостойкости изоляции указывают на паспортном щитке электродвигателя. Для типовых тепловых расчетов температуру окружающей среды принимают +40°С. Следовательно, мощность двигателя, указанная на паспортном щитке, соответствует нормированной температуре окружающей среды +40°С.
Температуры в наиболее нагретом месте изоляции не должны превышать указанных предельно допустимых значений температуры при работе электрооборудования в нормальном режиме при предусмотренной для этого режима максимальной температуре
охлаждающей среды.
Электродвигатель - электромеханический преобразователь. В самом двигателе в процессе преобразования часть энергии теряется и выделяется в виде теплоты, которая и вызывает его нагрев [7]. Естественно, что при выборе двигателя недостаточной мощности он перегревается, происходит интенсивное тепловое старение изоляции. Срок службы двигателя резко сокращается, понижается надежность работы, снижается фактическая перегрузочная способность. Установлено, что срок службы изоляции сокращается примерно в 2 раза на каждые 10 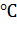 дополнительного повышения температуры изоляции сверх нормированной
дополнительного повышения температуры изоляции сверх нормированной 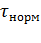 . Десятиградусное правило для
. Десятиградусное правило для 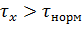 можно записать в виде:
можно записать в виде: 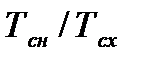 =
= 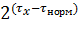 , (7.4)
, (7.4)
где 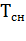 /
/ 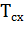 - сокращение срока службы
- сокращение срока службы 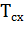 изоляции электрической машины по сравнению с нормированным сроком
изоляции электрической машины по сравнению с нормированным сроком
службы 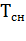 = 15... 20 лет.
= 15... 20 лет.
Выбор двигателя завышенной мощности в 1,5 раза и более ведет к резкому ухудшению его энергетических показателей (КПД, соs 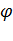 ) и неоправданному перерасходу средств и электроэнергии. Кроме того, из-за систематической недогрузки двигатель в период работы не прогревается до необходимой температуры. В условиях влажной окружающей среды изоляция двигателя во время длительных пауз в работе постепенно увлажняется и ее сопротивление понижается. Это может привести к электрическому пробою изоляции при включении двигателя и его преждевременному выходу из строя.
) и неоправданному перерасходу средств и электроэнергии. Кроме того, из-за систематической недогрузки двигатель в период работы не прогревается до необходимой температуры. В условиях влажной окружающей среды изоляция двигателя во время длительных пауз в работе постепенно увлажняется и ее сопротивление понижается. Это может привести к электрическому пробою изоляции при включении двигателя и его преждевременному выходу из строя.
Таким образом, мощность двигателя рассчитывают, прежде всего, исходя из обеспечения его нормированного нагрева, а затем в зависимости от характера нагрузки проверяют по дополнительным условиям: обеспечение пуска, устойчивой работы при перегрузках и т. д. для правильного выбора мощности двигателя по нагреву необходимо знать закон, по которому его температура изменяется во времени.
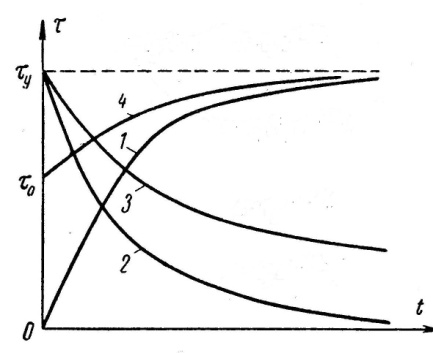
Рис.7.5. Графики нагрева и охлаждения электродвигателя.
В целях упрощения решения поставленной задачи допускают следующее: двигатель представляет собой однородное тело, температура которого во всех точках в любой момент времени одинакова, т.е. его теплопроводность равна бесконечности; теплоотдача двигателя пропорциональна первой степени превышения температуры; теплоту, отдаваемую излучением, из-за малости не учитывают; в рассматриваемый малый период времени нагрузка на валу двигателя, потери ё
мощности и температура окружающей среды неизменны [14].
На основании закона сохранения энергии с учетом принятых допущений составим уравнение теплового баланса электродвигателя для бесконечно малого интервала времени затрачена на нагрев самого двигателя, а другая часть будет отдана в окружающую среду.
Таким образом, справедливо равенство:
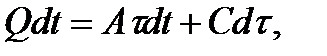 (7.5 )
(7.5 )
где Q - общее количество теплоты, выделяемое двигателем в единицу времени, Дж/с; С - теплоемкость двигателя, т. е. количество теплоты, необходимое для повышения температуры двигателя на 1°С, Дж/град; А - теплоотдача двигателя, т. е. количество теплоты, выделяемое двигателем в окружающую среду в единицу времени при разности температур, равной 1  С, Дж/с.град;
С, Дж/с.град; 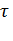 - превышение температуры двигателя над температурой окружающей среды °С.
- превышение температуры двигателя над температурой окружающей среды °С.
Выражение (7.5) представляет собой дифференциальное уравнение теплового баланса электродвигателя, причем уравнение с разделяющимися переменными. Процесс нагревания двигателя характеризуется зависимостью превышения температуры двигателя над температурой окружающей среды от времени: т = f(t). На основании
уравнения (7.5) найдем эту зависимость.
Разделим переменные:
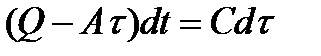
отсюда
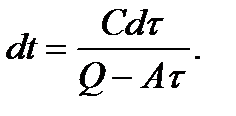 (7.6)
(7.6)
После интегрирования получаем:
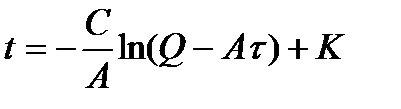 . (7.7)
. (7.7)
Определим постоянную интегрирования К из условия, что при t= 0 в общем случае начальное значение разности температур двигателя и окружающей среды 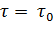
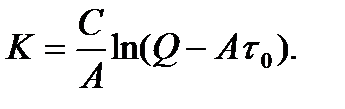
Подставим полученное значение К в уравнение (7.7):
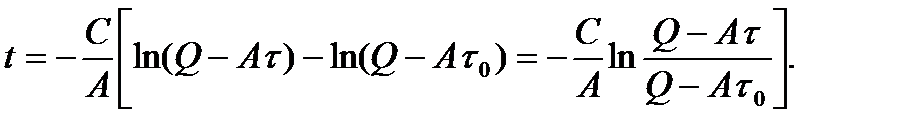 (7.8)
(7.8)
Решим уравнение (7.8) относительно величины 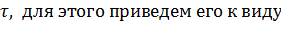 :
:
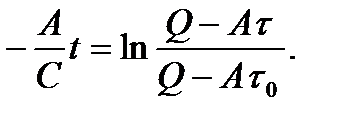
Потенцируя левую и правую части последнего равенства, получаем:
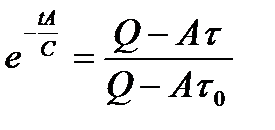
откуда
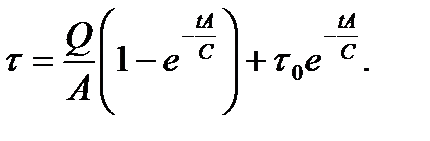 (7.9)
(7.9)
Обозначая в равенстве (7.9) С/А = 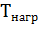 и Q/А =
и Q/А = 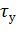 , получаем окончательный вид уравнения, определяющий закон изменения
, получаем окончательный вид уравнения, определяющий закон изменения
превышения температуры двигателя над температурой окружающей среды во времени:
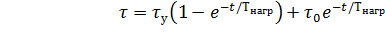 . (7.10)
. (7.10)
Если в начальный момент 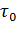 = 0,
= 0,
то уравнение нагрева принимает следующий вид
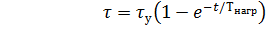 , (7.11)
, (7.11)
где 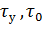 - превышение температуры двигателя соответственно
- превышение температуры двигателя соответственно
установившееся и в начальный момент.
Согласно уравнениям ( 7.10) и (7.11) на рис.7.5 построены
кривые 4 и 1.
Физический смысл величин  , и
, и 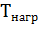 , входящих в последние равенства, становится ясным из анализа уравнений (7.9) и (7.10).
, входящих в последние равенства, становится ясным из анализа уравнений (7.9) и (7.10).
Действительно, при t = 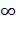
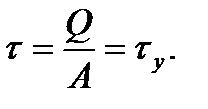 (7.12)
(7.12)
Следовательно, 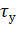 - это значение установившегося превышения температуры двигателя над температурой окружающей среды, которое достигается двигателем через бесконечно большое время.
- это значение установившегося превышения температуры двигателя над температурой окружающей среды, которое достигается двигателем через бесконечно большое время.
Входящую в уравнение (7.11) постоянную величину
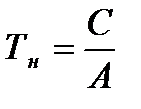 (7.13)
(7.13)
называют постоянной времени нагрева, так как она характеризует скорость нагревания двигателя. Постоянную 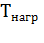 можно представить как интервал времени, в течение которого двигатель достиг бы установившейся температуры
можно представить как интервал времени, в течение которого двигатель достиг бы установившейся температуры 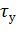 , если бы отдача теплоты в
, если бы отдача теплоты в
окружающую среду отсутствовала.
Действительно, при А = 0 уравнение (7. 5) примет вид:
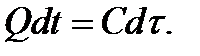 (7.14)
(7.14)
Считая, что нагрев двигателя начинается от температуры окружающей среды, т.е. 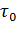 = 0, после интегрирования (7.14) получаем:
= 0, после интегрирования (7.14) получаем:
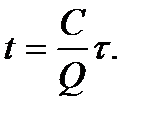 (7.15)
(7.15)
Подставив в (7.15) значение  =
= 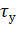 = Q/А, найдем продолжительность нагревания двигателя до установившейся температуры:
= Q/А, найдем продолжительность нагревания двигателя до установившейся температуры:
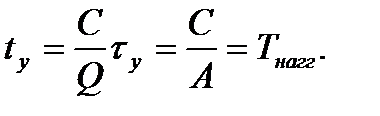 (7.16)
(7.16)
При различных нагрузках нагревание двигателя нагревание двигателя происходит по разным кривым, как это показано на рис.7.7. Постоянная времени нагрева двигателя остается неизменной.
Постоянные времени нагрева электродвигателя определяют различными методами.








