Графический метод расчета пусковых сопротивлений

Дата: 2025-06-02; Просмотры: 10

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Этот способ расчета дает наглядное представление о значениях добавочных сопротивлений, но имеет существенный недостаток -

точность расчетов зависит от точности построения пусковой диаграммы двигателя.

Электромеханические характеристики для двигателя постоянного тока с включенным в цепь якоря добавочным сопротивлением R_доб. приведены на рис. 2.15.

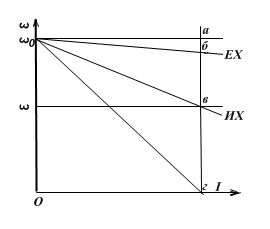
Рис.2.15. Электромеханические характеристики ДПТ НВ при введении добавочных резисторов в цепь якоря.

Уравнение ЭДС для номинального тока и частоты вращения ω

(точка в):

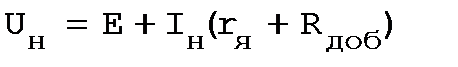
или

.

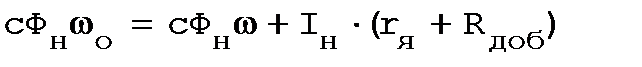Последнее выражение разделим на сФ_н:

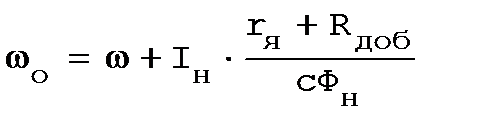. (2.39)

Из рис.2.15имеем:

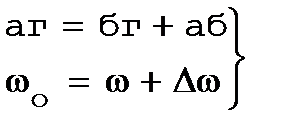(2.40)

Сравнивая выражения (2.39) и (2.40 ), запишем:

,

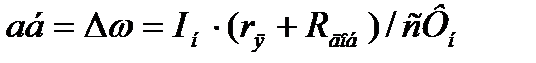следовательно, для постоянных значений I_н и сФ_н значение отрезка аб пропорционально 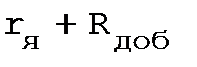. Если характеристика проходит через точку г, то все приложенноеU_н уравновешивается падением в

сопротивлении R_н:

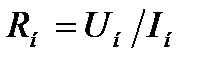(2.41)

R_н носит название номинального сопротивления, 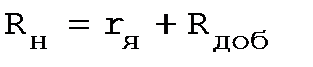. Номинальное сопротивление электродвигателя - это такое сопротивление якорной цепи, при котором в момент включения (при ω=0) в обмотке якоря протекает номинальный ток. Отрезок аг пропорционален R_н. Таким образом, по значению отрезка, отсекаемого характеристикой на линии номинального тока, можно рассчитать сопротивление якорной цепи. Но для этого необходимо знать масштаб

сопротивлений:

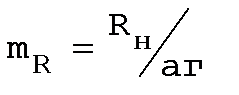или ,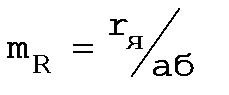

где 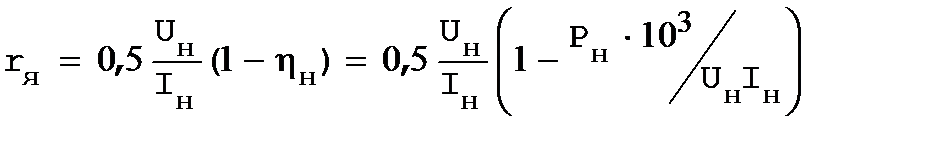; U_н, I_н, Р_н, - номинальные напряжение, ток и мощность двигателя.

Первый способ определения масштаба более точный, так как

отрезок аг больше, чем отрезок аб.

При расчете пусковых сопротивлений двигателя постоянного тока графическим методом возможны два варианта.

1.Число пусковых ступеней m задано.

По паспортным данным машины строим естественную электромеханическую характеристику по двум точкам (ω_o, М = 0) и (I_н, ω_н)

(рис. 2.16). Откладываем значения токов переключения I₁ и I₂.

Их значения необходимо обосновывать, исходя из требований технологии к электроприводу и коммутационной способности двигателя. Предельное значение тока I₁ берем равной (2...2,5)I_н. Ток I₂ = (1,2...1,3)I_н. Через точки, соответствующие значениям I₁ и I₂ на оси токов проводим две прямые, параллельные оси частоты вращения. Соединяем точки 1 и ω_о прямой линией, которая пересечется в точке 2 с током I₂.

Дальнейший порядок построения от точки 2 к 3 и т.д. виден из рис. 2.16. В результате построения необходимо попасть в точку пересечения естественной электромеханической характеристики и линии тока переключения I₁ (точку 7). Если совпадения не получилось или число ступней не равно заданному, то необходимо изменить значение тока I₂ или I₁ и повторить построение.

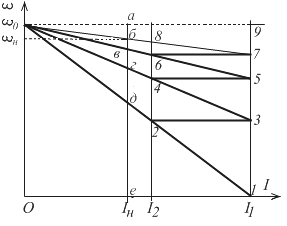
Рис. 2.16. Графический метод расчета сопротивлений пусковых

резисторов ДПТ НВ.

Определяем масштаб сопротивления:

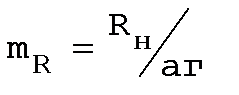или ; ;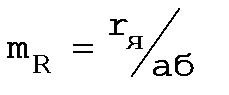

.

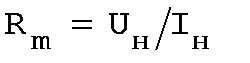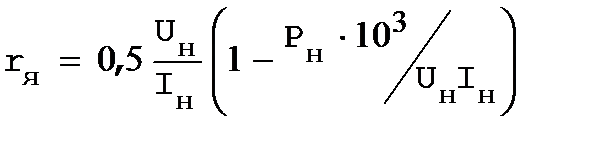Определяем значения пусковых сопротивлений ступеней:

; ; ; .

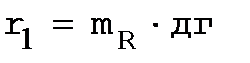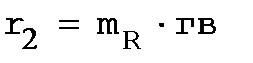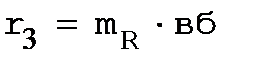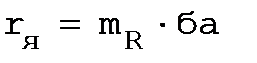Проверяем правильность расчета:

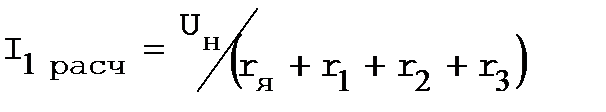
Полученное значение должно отличаться от заданного тока не более чем на 7...10%. При отклонении более 10% необходимо выполнить более тщательное построение и расчет.

2. Если число пусковых ступеней не задано, то в этом случае при построении необходимо попасть в точку пересечения линии тока I₁ и естественной электромеханической характеристики, а затем принять то число ступеней, которое получится.

Таким образом, процесс пуска двигателя в несколько ступеней, изображенный на рис. 2.16, характерен тем, что ток двигателя во время пуска колеблется в пределах от 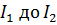. В начале пуска 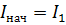, далее, по мере ускорения двигателя растет его ЭДС, вследствие чего начинает уменьшаться ток в цепи якоря двигателя, а следовательно, и момент двигателя. Когда ток достигает 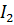выключается часть пускового реостата с таким расчетом, чтобы ток двигателя снова достиг значения 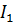и т.д.

По мере выведения пусковых резисторов сопротивление цепи якоря уменьшается, а следовательно, уменьшается и значение электромеханической постоянной, что приводит к уменьшению продолжительности пуска на каждой последующей ступени.

Глава 3.

Электроприводы с двигателями постоянного

тока по c ледовательного возбуждения

3.1. Особенности работы ДПТ ПВ

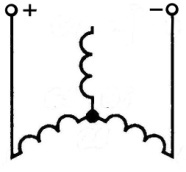
Двигатели постоянного тока последовательного возбуждения широко применяют на электротранспорте, в приводе подъемно-транспортных механизмов. Необходимо отметить, что такие двигатели применяют в качестве стартеров для двигателей вну­треннего сгорания. Двигатели последовательного возбуждения надежны по сравнению с другими машинами постоянного тока, так как они имеют обмотку возбуждения, выполненную проводом большого сечения, и с малыми напряжениями между витками. Схема включения в сеть приведена на рис.3.1 , откуда видно, что ток возбуждения равен току якоря, который зависит от нагрузки двигателя. Во время работы ток якоря изменяется от холостого хода до номинального значения (и более), следовательно, изменяется и поток возбуждения.

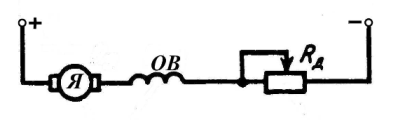
Рис. 3.1. Схема включения ДПТ ПВ: ОВ – обмотка возбуждения;

Я – обмотка якоря.
Вследствие этого невозможно дать аналитические выражения механической и электромеханической характеристик для конкретного двигателя, по которым можно было бы построить их графики. Для анализа механической характеристики машины постоянного тока последовательного возбуждения реальный график намагничивания заменяют идеализированным - ломаным, линейным (рис.3.2 ).

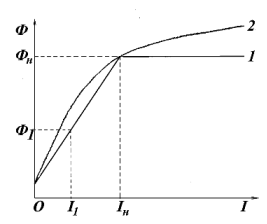
Рис. 3.2. Кривые намагничивания машин постоянного тока

последовательного возбуждения: 1 – идеализированная характери

стика; 2 – реальная характеристика.

Предположим, что двигатель работает на идеализированной характеристике (а) с нагрузкой 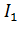, меньшей 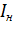(система не насыщена). Так как эта часть характеристики линейна, то

Ф = кI, (3.1)
где к – коэффициент пропорциональности, к = Ф /Iн.
Электромагнитный момент:
М = сФI = скI. (3.2)
Уравнение ЭДС:
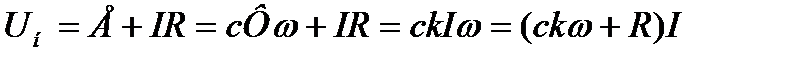. (3.3)
где R - сопротивление якорной цепи.
Из выражения (3.3) определяем электромеханическую

характеристику:
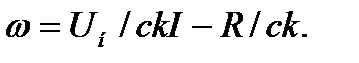(3.4)
Из уравнения электромагнитного момента определим значение тока и подставим его в выражение электромеханической характеристики:

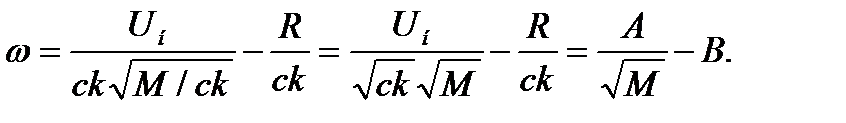(3.5)
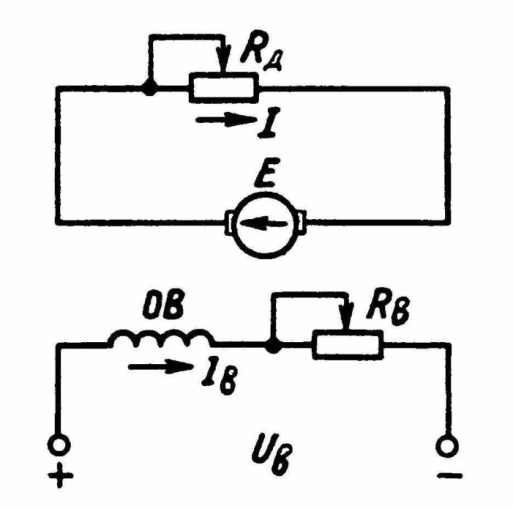
Зависимость между моментом и частотой вращения при насыщенной магнитной системе имеет гиперболический характер. Это справедливо для малонагруженных электрических двигателей, ток которых меньше номинального. При токе больше номинального наступает насыщение, поток двигателя не изменяется и механическая характеристика практически становится линейной. На холостом ходу остаточный поток равен (0,02…0,09)Ф, следовательно, и характеристика а этой части становится близкой к линейной. Таким образом, характеристику двигателя постоянного тока можно разделить на три участка: 1, II, III (рис.3.3 ).

Нижний участок характеристики – 1 от = 0 до линейный и соответствует насыщению магнитной цепи машины (Ф = const).

Средний – П - соответствует гиперболической зависимости момента от частоты вращения, для которой ось ординат является

асимптотой.

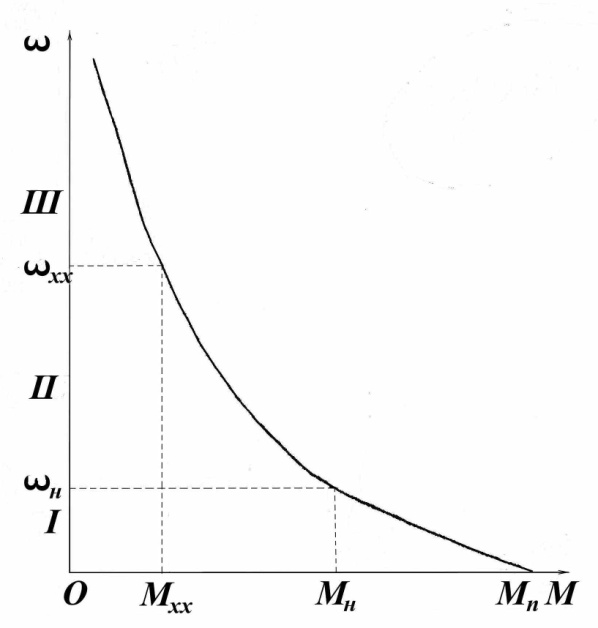
Рис. 3.3. Механическая характеристика двигателя последовательного

возбуждения.

Верхний - Ш участок имеет почти линейный характер и соответствует остаточному магнитному потоку. Особенностью механической характеристики двигателя последовательного возбуждения является ее большая крутизна в области малых значений момента.
Значительное увеличение частоты вращения при малых нагрузках обусловливается соответствующим уменьшением магнитного потока.
Уравнение (3.5) дает лишь общее представление о механической характеристике двигателя последовательного возбуждения. При расчетах этим уравнением пользоваться нельзя, так как машин с ненасыщенной магнитной системой обычно в современной практике не строят. Вследствие того, что реальные механические характеристики сильно отличаются от кривой, выраженной уравнением (3.5), построение характеристик приходится выполнять графо-

аналитическими способами.

3.2. Естественные электромеханическая и механическая

характеристики ДПТ ПВ

Электромеханическая и механическая характеристики ДПТ ПВ являются естественными, eсл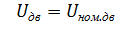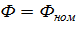и , и 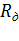= 0. На практике для построения естественных характеристик используют обобщенные зависимости (универсальные характеристики) для двигателей данного типа (рис.3.4).Универсальная характеристика

дается в относительных величинах:
; ;

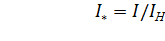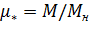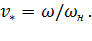
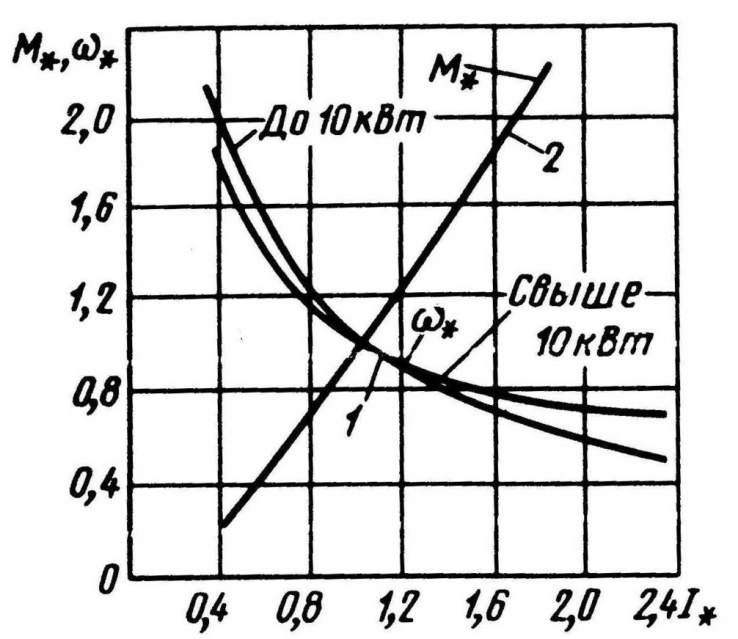
Рис. 3.4.Универсальные характеристики двигателей ДПТ ПВ.

где I, M и 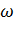- текущие значения тока, момента и угловой скорости двигателя; 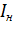, 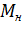и 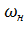- номинальные значения тока, момента и

угловой скорости двигателя.
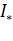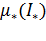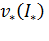Для построения характеристик двигателя задаемся несколькими относительными значениями тока двигателя на универсальной характеристике и по кривым и определяем значения 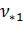и 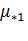[18]. Абсолютные значения тока, угловой скорости

и момента: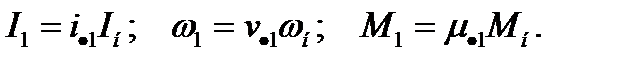
При построении характеристик стремятся значения относительных величин выбирать по возможности равномерно. Результаты расчетов заносим в табл.3.1.

Затем задаемся значением 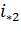и определяем координаты второй точки. Результаты заносим в ту же таблицу. Таким образом, для заданного диапазона изменения угловой скорости или тока получим

серию расчетных точек (не менее пяти).

Таблица 3.1

Данные для расчета электромеханической и механической

характеристик ДПТ ПВ

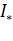
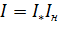
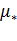
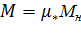
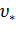
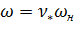
3.З. Искусственные механические характеристики ДПТ ПВ

Механические характеристики ДПТ ПВ являются искусственными в следующих случаях:

в цепь якоря последовательно включают добавочный резистор;
изменяют напряжение питания машины;
параллельно якорю или обмотке возбуждения включают резистор.
На искусственных механических характеристиках двигатель работает при регулировании частоты вращения, ограничении пусковых токов и во многих других случаях, например, при снижении напряжения при пуске мощного двигателя. Искусственные механические

характеристики строят различными методами.
Аналитический метод построения искусственной характеристики при изменении добавочного сопротивления в якорной цепи.
Добавочное сопротивление в якорную цепь вводится для ограничения пускового тока или регулирования частоты вращения. Для любого значения частоты вращения и соответствующего тока I двигателя на естественной электромеханической характеристике уравнение ЭДС можно записать в виде
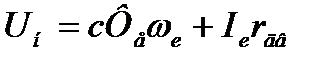. (3.6)
где 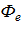- магнитный поток двигателя, соответствующий току .

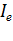При введении в цепь якоря добавочного сопротивления двигатель будет работать на искусственной характеристике. Тогда

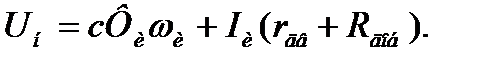(3.7)

где 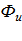, , 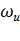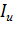- магнитный поток, угловая скорость и ток

двигателя на искусственной характеристике.
Определим значения угловых скоросте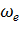й и 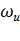из уравнений (3. 6) и (3.7 ) и возьмем их отношение:

(3.8)

а б

Рис.3.5. Электромеханические характеристики ДПТ ПВ при введении

добавочного резистора.

Если у двигателя на естественной и искусственной электромеханических характеристиках токи равны, т.е. 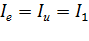, то равны и

потоки возбуждения: 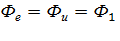(рис.3.5 ).

Выражение (3.8) с учетом сказанного запишем следующим образом:
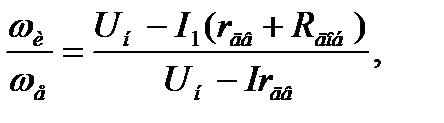(3.9)

откуда

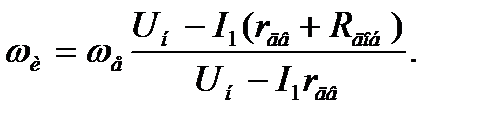(3.10)

Таким образом, задаваясь на естественной электромеханической характеристике значениями тока 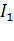и угловой скорости 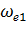, определяем угловую скорость 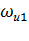на искусственной характеристике при введенном в цепь якоря добавочном сопротивлении для того же тока.
Построение искусственных электромеханических и механических характеристик при введении в цепь якоря добавочного сопротивления выполняем следующим образом. По универсальной характеристике и паспортным данным двигателя строим естественные механическую и электромеханическую характеристики. Определяем значение

сопротивления резистора :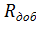
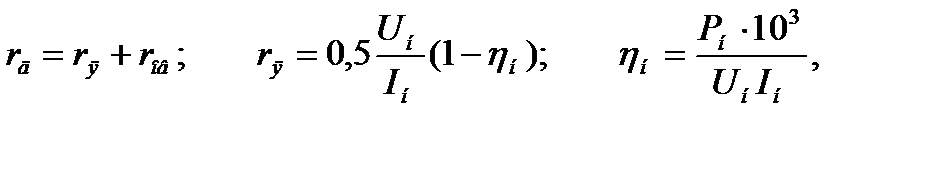(3.11)

где 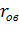- сопротивление обмотки возбуждения; 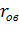= 0,5 ;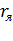

.
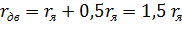По выражению (3.10 ) строим искусственную электромеханическую характеристику для заданного сопротивления 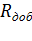. Для этого

задаемся током 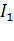и определяем 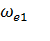(рис.3.6).
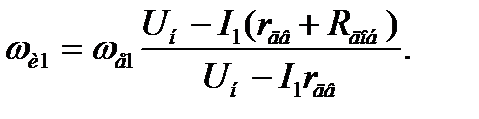(3.12)

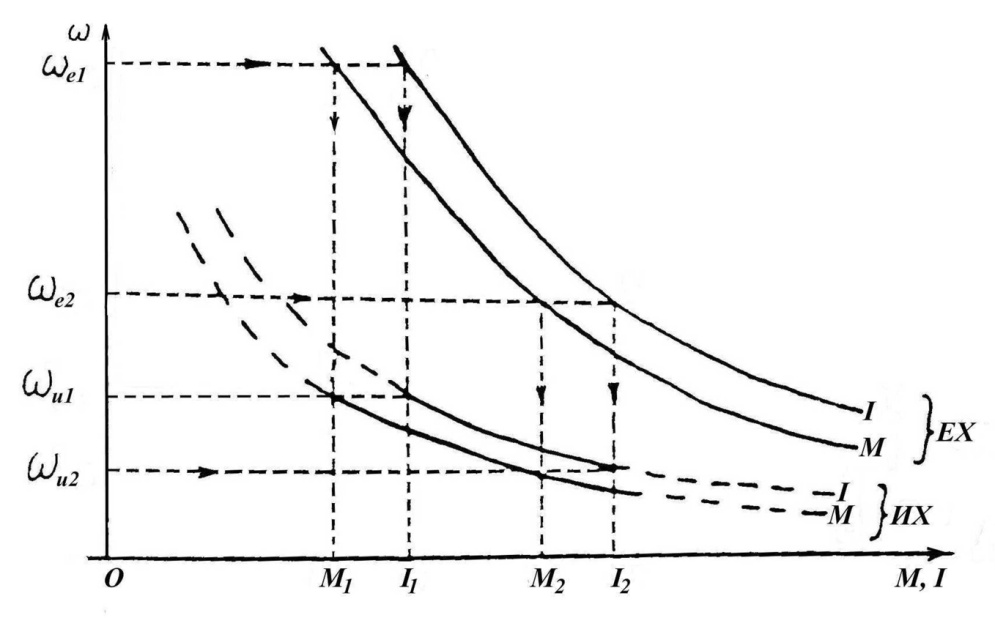
Рис. 3.6. Построение искусственных механических и

электромеханических характеристик ДПТ ПВ аналитическим

методом при включении добавочного сопротивления.

После этого принимаем значения тока: (не менее пяти точек в рассматриваемом диапазоне) и рассчитываем соответствующие угловые скорости и т.д. По полученным данным строим

искусственную электромеханическую характеристику.
Для построения искусственной механической характеристики поступают следующим образом: при угловой скорости (токе ) значение момента двигателя равно 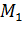. На искусственной электромеханической характеристике при угловой скорости значение тока не изменилось, следовательно, не изменился и момент, т.е. 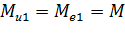. Аналогично определяем моменты для 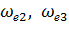и т.д. Соединив полученные точки, получим искусственные механическую и электромеханическую характеристики (рис.3.6).
Графический метод построения искусственных механических характеристик двигателей последовательного возбуждения заключается в в следующем. Если ток двигателя последовательного возбуждения постоянен, т.е. I = const, то постоянным будет и поток возбуждения (Ф = соnst). Из уравнения ЭДС двигателя определяем зависимость

сопротивления якорной цепи от угловой скорости:
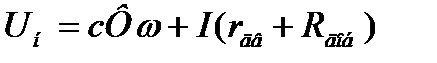(3.13)

откуда

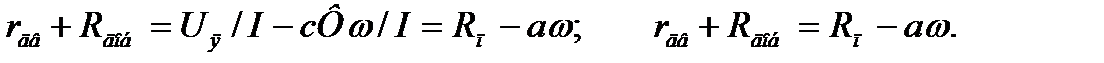(3.14)

3начит, при одном и том же токе двигателя между угловой скоростью и сопротивлением существует линейная зависимость.
Для построения графика искусственной механической характеристики в требуемом диапазоне задаемся пятью-шестью значениями токов: 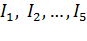. Графики изменения сопротивления от угловой скорости

R = f( 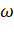) при заданных значениях токовстроим во втором квадранте по двум точкам. Для тока 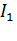координаты первой точки ( 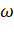= 0; 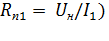; второй - ( ). Для тока координаты следующие: первой точки ( 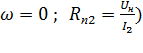; второй 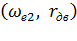и т.д. Таким образом, получаем семейство линейных характеристик R = f(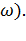
Искусственную электромеханическую характеристику при заданном добавочном сопротивлении 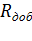строят вследующем порядке (рис.3.7 ): от сопротивления 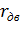дополнительно по оси R откладываем в масштабе 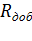(точка б); через точку б проводим прямую, параллельную оси . Эта прямая пересекает графики 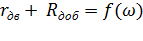в пяти точках: 1”, 2”, 3, 4”, 5”. Эти точки определяют значения угловой скорости двигателя при введенном добавочном сопротивлении 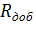для токов 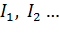Для графического построения электромеханической характеристики 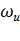= (I) проводим прямую, параллельную оси I ‚ через 1” до пересечения с точкой в точке 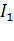, которая лежит на искомой электромеханической характеристике = f (t ).

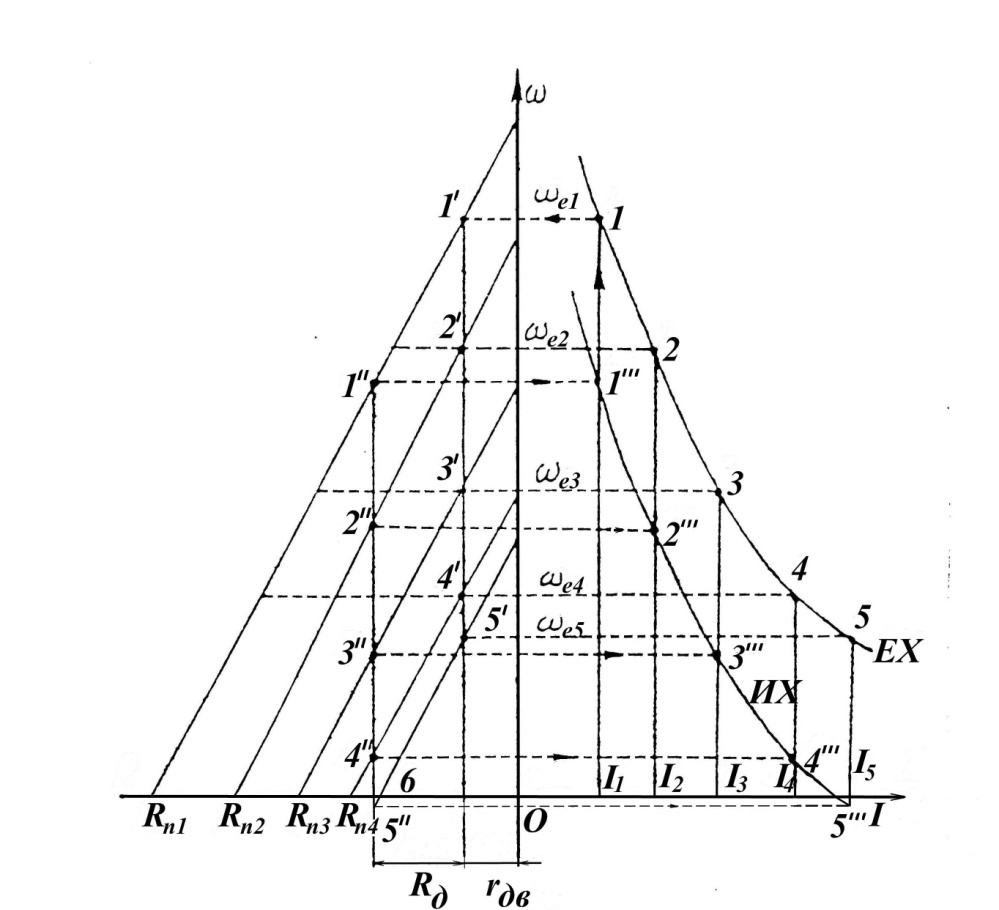
Рис. 3.7. Графический метод построения электромеханической характеристики ДПТ ПВ при изменении добавочного резистора.
Аналогичные построения выполняются для точек т.д. Соединив эти точки плавной линией, получим график электромеханической характеристики при добавочном сопротивлении .
Механическую характеристику строят так же, как при

аналитическом методе.
Искусственные механические характеристики двигателя последовательного возбуждения при изменениях напряжения отражают изменения момента и угловой скорости при регулировании частоты вращения двигателя и при ограничении пускового тока. Для этого используется специальный регулируемый источник: система Г-Д, управляемый тиристорный выпрямитель и т.д. Механические характеристики при изменениях напряжения можно построить по полученным ранее соотношениям. Уравнение ЭДС двигателя (3.7 ) при работе на искусственной характеристике для заданного тока I :

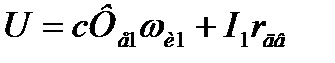. (3.15)

В этом случае необходимо в уравнении (3.7) принять 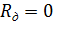и s w:ascii="Cambria Math"/><w:i/><w:sz w:val="28"/></w:rPr><m:t>С„</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 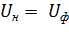. Тогда

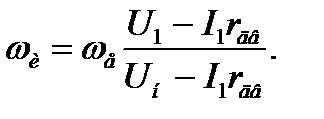(3.16 )

Для заданного значения 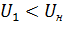примем значения токов 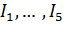и определим угловые скорости 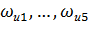по выражению (3.16). Построим искусственную электромеханическую характеристику. Механическая характеристика строится аналогично.

3.4. Тормозные режимы ДПТ ПВ

ДПТ ПВ может работать в двух тоpмозных режимах: противовключения и динанамического тоpможения.

В режиме противовключения ДПТПВ напряжение сети и ЭДС совпадают по знаку. Для ограничения значения тока в цепь якоря вводится добавочный резистор. Механические характеристики для этого режима располагаются во втором и четвертом квадрантах.

Режим противовключения возможен в двух случаях:

1.При работе двигателя с активным моментом сопротивления,­ например, движение лебедки, поднимающей груз. Здесь 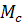– момент сопротивления, создаваемый грузом (рис.3.8).

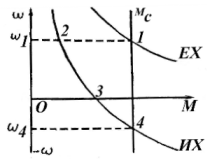
Рис. 3.8. Характеристика режима противовключения ДПТ ПВ при включении добавочного резистора в цепь якоря.

Подъем груза идет со скоростью ω₁ (точка 1). Включаем в цепь якоря добавочное сопротивление R_добl , двигатель переходит на искусствeннyю механическую характеристику (точка 2). Под дейст­вием груза происходят тоpможение двигателя до ω₃ = 0. В точке 3 , поэтомy под действием груза двигатель начинает вращаться в обратнyю сторону, против включения, и в точке 4 . Двигатель будет работать с постоянной угловой скоро­стью ω₄ в режиме противовключения, опуская груз.

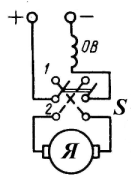
Рис.3.9. Реверсирование двигателя ДПТ ПВ.

2.При реверсе двигателя, который осуществляют изменением полярности подведенного к якорю напряжения (рис.3.9). Направление тока в обмотке возбуждения не меняют, с тем чтобы не перемагнитить систему (рис. 3.10 ).

Механические характеристики для этого случая изображены на pис. 3.10.

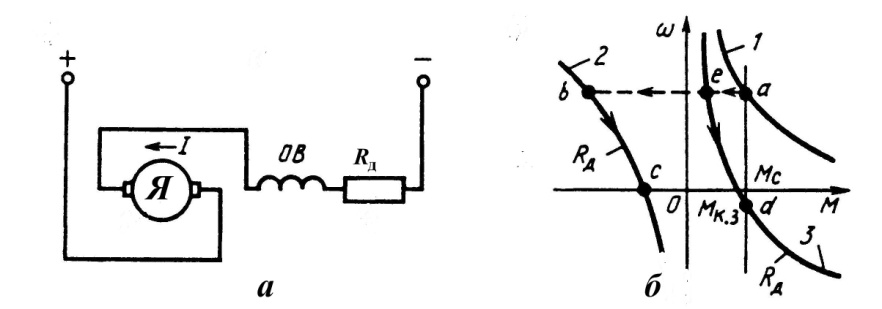
Рис.3.10. Механические характеристики ДПТ ПВ

при реверсе в режиме противовключения..

При переключении обмоток якоря под действием сил инерции угловая скорость в первый момент не изменится. Не меняются направление тока в обмотке возбуждения и знак потока возбуждения. Ток якоря меняет свое направление, поэтому момент двигателя становится отрицательным и характеристика располагается во втором квадранте. Этот момент тормозной, так как момент и угловая скорость имеют разные знаки. При реверсе ЭДС двигателя и напряжение сети совпадают по знаку, поэтому для ограничения тока в цепь якоря включают добавочный резистор, и характеристика получается пологой. В режим противовключения характеристика двигателя располагается

между точками б и с.
Уравнение ЭДС для режима противовключения:

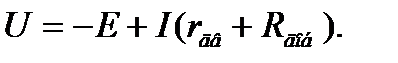(3.17)
Умножим на ток I левую и правую части:
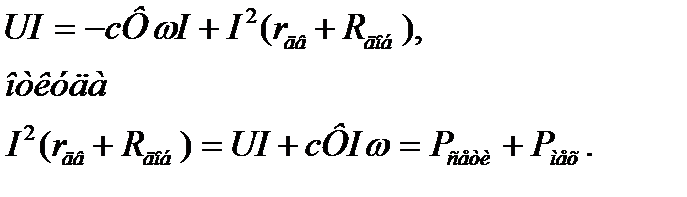(3.18)
Из этого выражения следует, что энергия, подводимая из сети и с вала двигателя, полностью теряется в резисторах 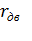и .
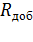Динамическое торможение ДПТ ПВ можно осуществить двумя способами: с независимым возбуждением и с самовозбуждением.
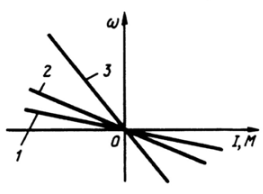
Торможение с независимым возбуждением получают следующим образом: обмотку якоря замыкают на добавочный резистор, а обмотку возбуждения включают в сеть. В этом случае имеем рассмотренное ранее динамическое торможение двигателя независимого (параллельного) возбуждения. Схема и механические характеристики для этого случая приведены на рис.3.11.

а б

Рис.3.11. Механические характеристики ДПТ ПВ в режиме

динамического торможения с независимым возбуждением: а - схема;

б – механические характеристики.

В режиме динамического торможения с самовозбуждением якорь включают последовательно с обмоткой возбуждения через добавочный резистор. Чтобы не размагничивать систему при данном способе торможения, переключают якорь и оставляют прежним направление тока в обмотке возбуждения (рис.3.12).

Остаточный магнитный поток машины в обмотке якоря наводит ЭДС. После переключения якоря направление тока обмотки воз­буждения остается прежним, и остаточный поток сyммиpуется с потоком, созданным током возбуждения. Значение наведенной ЭДС возрастает, одновременно растет и ток. Для его ограничения необходимо добавочное сопротивление R_доб, Знак создаваемого момента будет отрицательным из-за смены направления то­ка в якоре, следовательно, для рассматриваемого направления вращения имеем тоpмозной режим. Механическая характеристика в режиме динамического торможения будет нелинейной, как и для двигательного режима (рис.3.13)

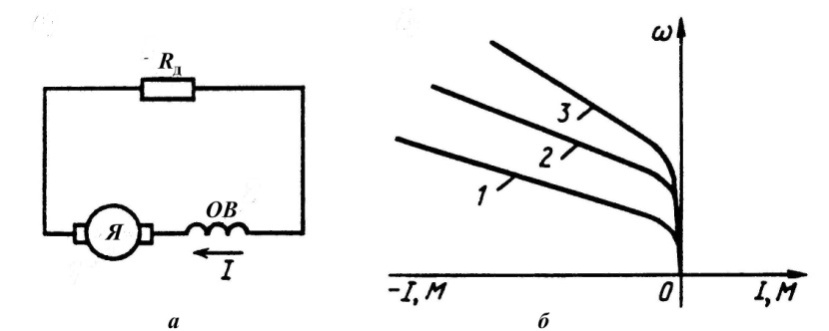
Рис.3.13. Механические характеристики ДПТ ПВ в режиме

динамического торможения с самовозбуждением.

Как показывает Москаленко, В.В. [12], особые свойства приобретает электродвигатель последовательного возбуждения при шунтировании обмотки якоря резистором 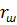(рис.3.14). Ток в обмотке

возбуждения

,

где 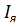- ток якоря, А; 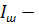ток в шунтирующем резисторе, А.

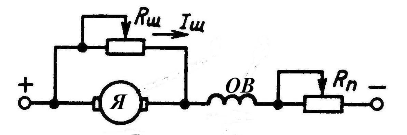
Рис.3.14. Схема включения ДПТ ПВ при шунтировании якоря

добавочным резистором.

В целях упрощения рассуждений можно принять, что в электродвигателе действует два магнитных потока: поток 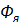, созданный током якоря, зависящий от нагрузки электродвигателя, и поток 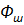, созданный током 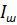, не зависящий от нагрузки электродвигателя.
Наличие магнитного потока 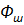делает возможным в электродвигателе последовательного возбуждения режим холостого хода. Значение частоты вращения идеального х.х. в таком электродвигателе тем меньше, чем меньше значение сопротивления резистора .
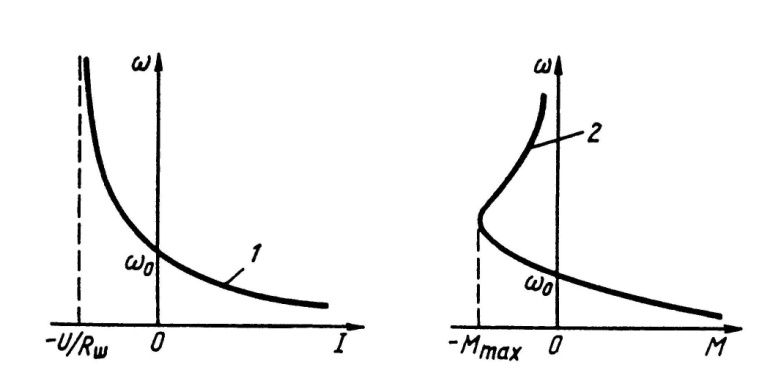
Электродвигатель последовательного возбуждения с шунтирующим резистором может работать в режиме генераторного торможения с отдачей энергии в сеть постоянного тока. Характеристики для этого режима работы представлены на рис. 3.16.

а б

Рис.3.15. Электромеханическая – а и механическая - б характери стики ДПТ ПВ при шунтировании якоря добавочным резистором.

3.5. Расчет пусковых и тормозных резисторов ДПТПВ

В основу определения пусковых и тормозных сопротивлений двигателя последовательного возбуждения положен графический метод построения характеристик [18].

1) в первом квадранте (рис.3.17) строим естественную

электромеханическую характеристику I = f(ω) по паспортным данным и универсальной характеристике;

2) принимаем токи переключения I₁ и I₂. Как и для двигателя независимого возбуждения, значения токов переключения определяется требованием технологии и условиями коммутации двигателя. Если время пуска двигателя не влияет на производительность рабочей машины, то значения пусковых токов может быть в области номинального тока. Если время пуска влияет на производительность рабочей машины, то

I₁ = (2,0…2,5)I_ном; I₂ = (1,2…1,5)I_{ном .} (3.19)

3) во втором квадранте откладываем сопротивление R_дв

R_дв = 1,5 U_н/I_н ∙ (1 - P_н∙10³/U_нI_н). (3.20)

4) для принятых токов переключений сопротивления определяем при 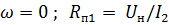. Полученные значения R_п1 и R_п2 откладываем на оси сопротивлений во втором квадранте.

5) через точки 1 и 2 (пересечение линий токов I₁ и I₂ с естественной электромеханической характеристикой) проводим прямые, параллельные оси тока до пересечения с линией 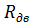в точках 1' и 2'. Проводим линии R_П1 - 1' и R_П2 - 2'. Затем восстанавливаем перпендикуляр из точки R_ПI до пересечения в точке 3. Через точку 3 проводим прямую, параллельную оси сопротивлений, до пересечения в точке 4 и т.д. Построение ломаной линии должно закончиться в точке 1. Если этого не получилось, необходимо изменить значения I₁ и I₂ и все пов­торить. График изменения тока двигателя I(ω) при пуске пока­зан в первом квадрате на рис. 3.17 . Значения добавочных соп­ротивлений берем из построения:

R₁ = l₃₄ ∙ m_R ; R₂ = l' ₅₁ ∙ m_R

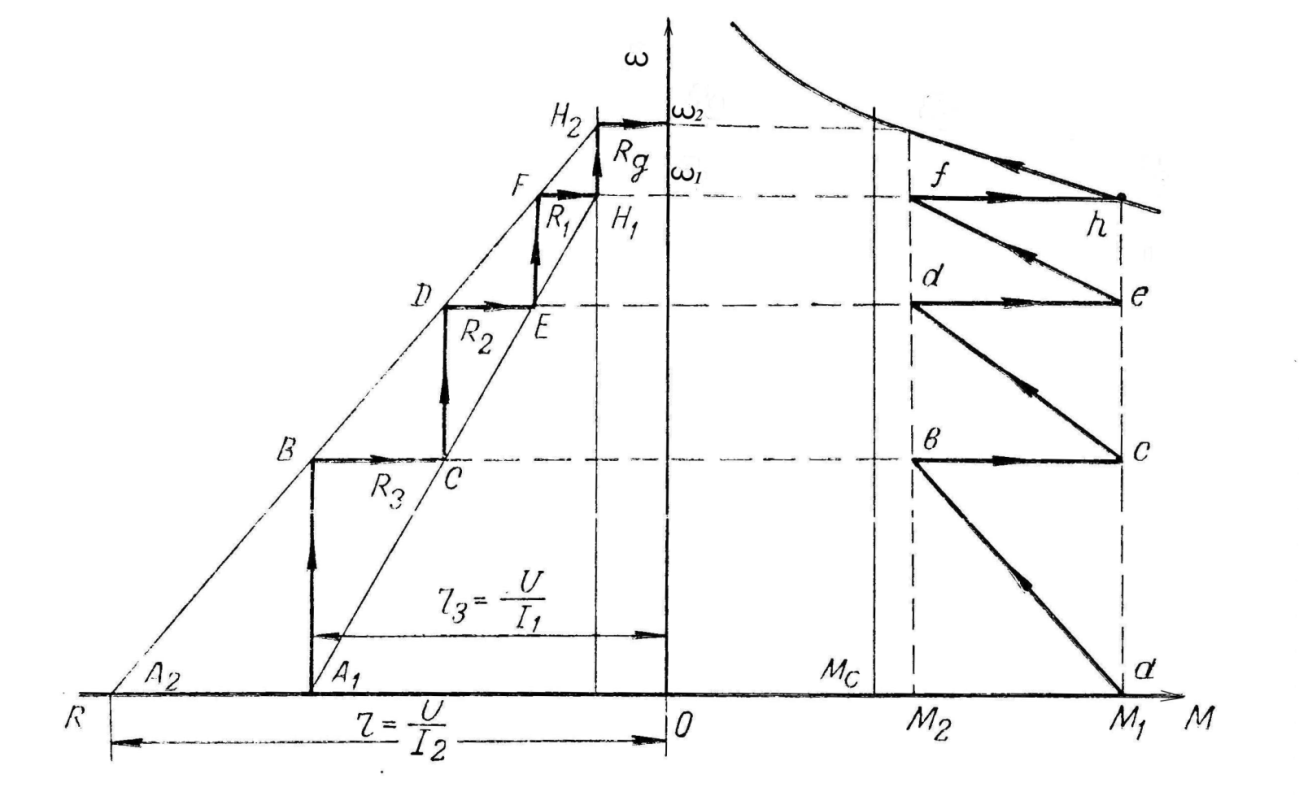
Рис. 3.16. Графический метод расчета пусковых резисторов ДПТ ПВ.

Правильность расчетов пусковых сопротивлений проверяем следующим образом:

1) определяем суммарное сопротивление якорной цепи:

ΣR = R_дв+ R_I + R₂ +...

2) определяем ток I = U_н/ΣR и сравниваем его с пусковым I₁.

Должно быть: I = I₁

Значение тормозного сопротивления в режиме противовключе­ния определяем аналитическим и графическим методами. Предва­рительно должны быть заданы ток I₁ и частота вращения ω_пв

Двигателя в режиме противовключения.

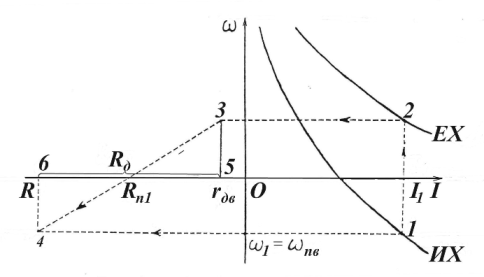
Рис.3.17. Графический метод расчета тормозного резистора.

По паспортным данным двигателя и универсальной характеристике

строим ω_ест = f (I) (рис. 3.17). Определим R_дв и R_п1 = U_н/I₁. Откладываем эти значения на оси сопротивления во втором квадранте. Через точку I₁ на оси токов проводим прямую, параллельную оси ω , до пересечения графика электромеханической характеристики в точке 2. Затем определяем точку 3. Через точки 3 и R_п1 проводим прямую до пересечения в точке 4. Добавочное сопротивление в этом режиме : R_доб = l₅₆ ∙ m_R .

Глава 4.

Асинхронный электропривод
Асинхронный электропривод широко применяется в сельскохозяйственном производстве благодаря надежности и простоте конструкции, дешевизне и высокому КПД асинхронного двигателя. Совершенствование асинхронного электропривода в настоящее время идет по трем направлениям: 1. Совершенствование электродвигателя; 2. Совершенствование соединительных устройств; З. Совершенствование преобразовательных устройств.
4.1 . Уравнение механической и электромеханической

характеристик асинхронного двигателя

Исследование и анализ механических характеристик осуществляют по эквивалентным схемам замещения. Наиболее целесообразной для анализа механических характеристик является Г-образная схема замещения, у которой намагничивающий контур вынесен на зажимы первичной цепи (рис. 4.1).

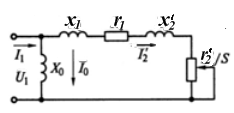
Рис.4.1. Упрощенная схема замещения асинхронного

двигателя.
Схема замещения построена для одной фазы при следующих

допущениях:
1) параметры всех цепей постоянны, т.е. вторичное приведенное сопротивление 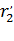не зависит от частоты тока ротора 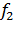, а насыщение, стали машины не влияет на реактивное сопротивление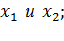
2) полная проводимость намагничивающего контура неизменна и намагничивающий ток пропорционален приложенному напряжению;
3) добавочные и магнитные потери в статоре не учитываются;
4) не учтены моменты, создаваемые высшими гармоническими

составляющими магнитодвижущей силы.
Обозначения элементов схемы замещения:
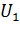- фазное напряжение обмотки статора, В; 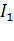- фазный ток статора, А; 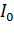- ток намагничивания, А; 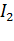- ток ротора, приведенный к напряжению статора. А; 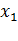- реактивное сопротивление обмотки статора, Ом; 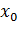- реактивное сопротивление контура намагничивания, Ом;

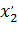- реактивное сопротивление ротора, приведенное к напряжению статора, Ом; 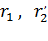- активное сопротивление обмотки статора электродвигателя, приведенные сопротивления ротора, Ом; z - полное сопротивление обмотки статора, Ом; s - скольжение ротора,
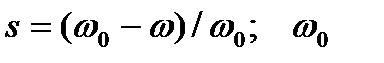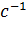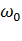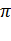- синхронная частота вращения, ; = 2 f/p,

р - число пар полюсов в фазной обмотке.
Параметры цепи ротора приведены (пересчитаны) к цени статора, что позволяет изобразить эти две цепи на схеме соединенными электрически. Приведение выполнено с помощью коэффициента трансформации АД по ЭДС.

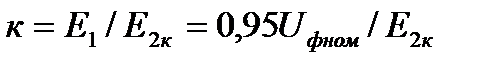, (4.1)

где 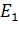и 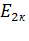- фазные ЭДС статора и ротора при неподвижном роторе. 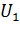- фазное номинальное напряжение сети.
Расчетные формулы приведения имеют вид.

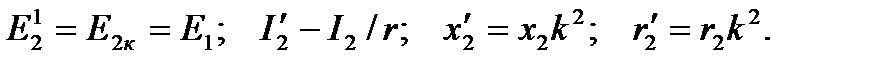(4.2)
Из схемы замещения ток ротора :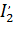
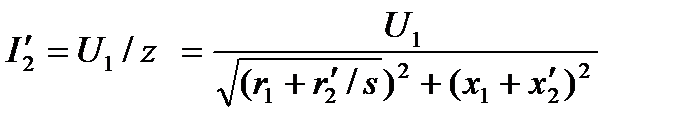. (4.3)

Примем и преобразуем выражение (4.3):
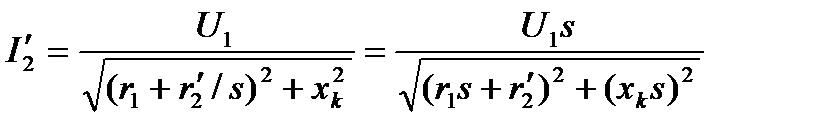. (4.4)

Полученное выражение является электромеханической характеристикой асинхронного двигателя. Оно показывает, что сила тока ротора двигателя с учетом принятых допущений определяется только скольжением s (или частотой вращения 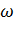). Так, при s = 0, когда ток ротора 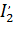= 0. В этом случае обмотка ротора неподвижна относительно магнитного поля статора и в ней не наводится ЭДС .
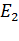По мере увеличения скольжения s (уменьшения частоты вращения 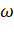) увеличивается 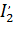и при остановке ротора ( 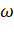= 0 , s = 1) ток 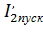становится максимальным . При этом в обмотке статора протекает пусковой ток
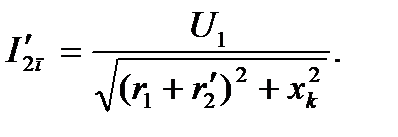(4.5)

Пусковой ток асинхронного двигателя превосходит номинальное значение в 5...10 раз. Кратность пускового тока I_пуск/ I_ном = i_п обычно приводится на щитке двигателя и в ка­талогах. Это очень важный показатель двигателя, так как от кратности зависят падение напряжения в сети, сечение питаю­щих проводов, мощность источника, выбор коммутирующих, защи­тных аппаратов. Асинхронный двигатель потребляет из сети активную мощность Р₁, которая преобразуется в электромагнит­ную Р_эм, передаваемую ротору, и теряется в намагничивающем контуре Р_μ, в меди обмоток статора Р_м1:

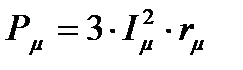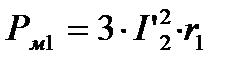; . (4.6)

Из схемы замещения (рис. 4.1) видно, что Р_эм расходуется в активном сопротивлении r^`₂/s:

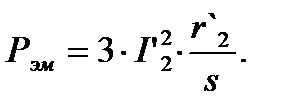(4.7)

Учитывая (4.4), можно записать:

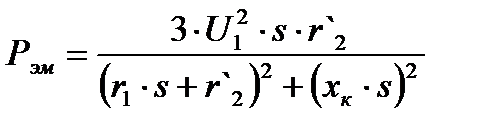. (4.8)

Из курса «Электрические машины» известно, что электромагнитную мощность, передаваемую из статора в ротор, определяют по выражению:

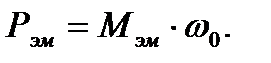(4.9)

где М_эм – электромагнитный момент статора;

Решив совместно выражения (4.8) и (4.9) получим:

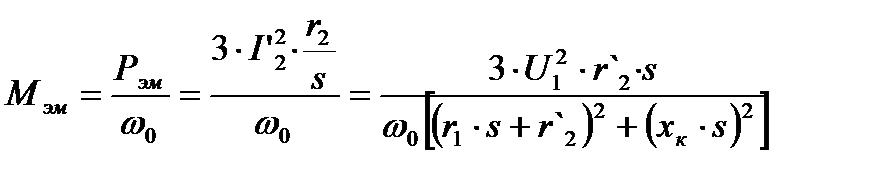. (4.10)

Это уравнение механической характеристики асинхронного двигателя. Для простоты написания в дальнейшем М_эм обозначили М. График механической характеристики имеет максимум, кото­рый наступает при определенном значении скольжения 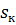для определения величины этого максимума и соответствующего значения скольжения 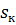возьмем производную по скольжению и приравняем ее к нулю:

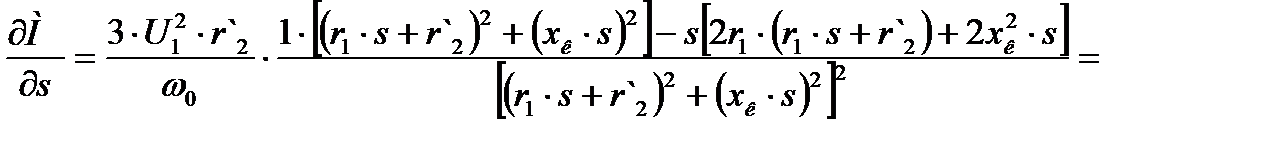
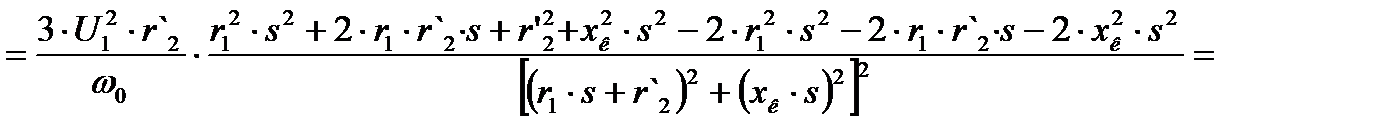
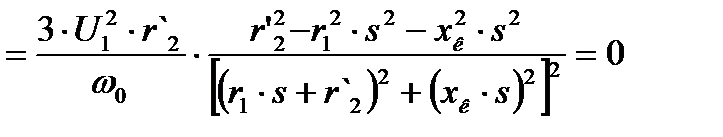. (4.11)

Частная производная 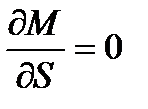при 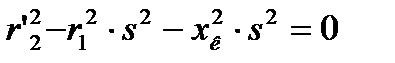. Отсюда определим скольжение s = s_к, при котором момент двигателя имеет максимум:

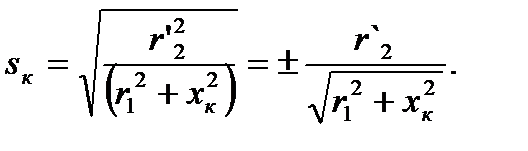(4.12)

Знак плюс относится к двигательному режиму, знак минус – к тормозному. Подставим значение s_к со знаком «+» в уравнение механической характеристики асинхронного двигателя (4.10) :

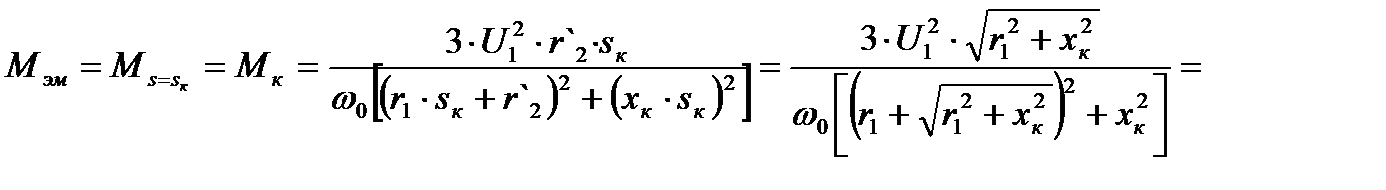
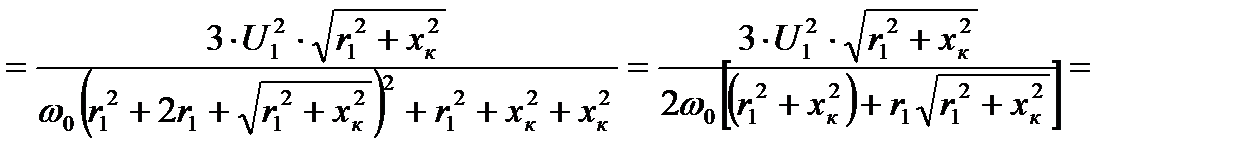
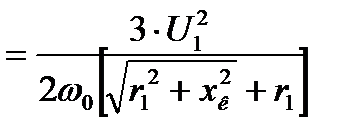. (4.13)

При s = s_к

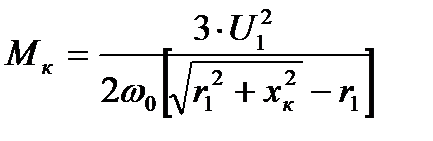. (4.14)

Если скольжение s_к отрицательно (в тормозном режиме), то

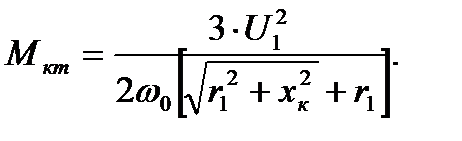
Если изменять значение скольжения ротора двигателя в пределах 0 ≤ s ≤ 1, то с учётом s_к и М_к график механической характеристики, построенной по выражению (4.10), имеет вид, изображённый на рис. 4.2. Момент М_к называется критическим, так как при нагрузке на валу, превышающий это значение, двигатель остановится ( иногда говорят «опрокинется» ) или будет вращаться в обратную сторону.

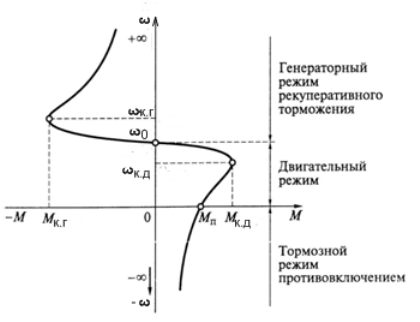
Рис. 4.2. Механическая характеристика асинхронного двигателя.

Если сравнить выражения критического момента для двигательного и тормозного режимов при равенстве сопротивлений r₁ и х_к, то окажется, что в тормозном режиме критический момент несколько больше. Физическое объяснение этого явления состо­ит в том, что за счет падения напряжения (значит, и мощности) в активном сопротивлении статора r₁ значение критическо­го момента в двигательном режиме будет меньше, чем в тормоз­ном. Для асинхронных двигателей мощностью 20 кВт и более активное сопротивление статора r₁ на порядок меньше индуктивного х_к. Поэтому значением r₁ можно пренебречь (приравнять к нулю). В этом случае:

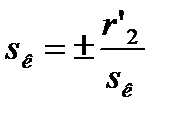(4.15); 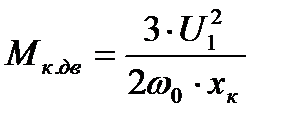(4.16); 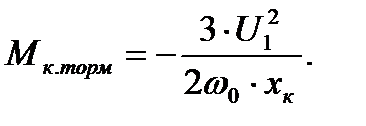(4.17)

4.2. Расчётное выражение механической характеристики

асинхронного двигателя

Уравнение механической характеристики асинхронного двигателя (4.10) затруднительно использовать для практических рас­четов, так как обычно неизвестны величины сопротивлений r₁, r`₂ и х_к. Необходимо получить выражение, в котором использовались бы паспортные данные двигателя. для этого поделим соответственно левую и правую части формулы (5.6) на (5.8):

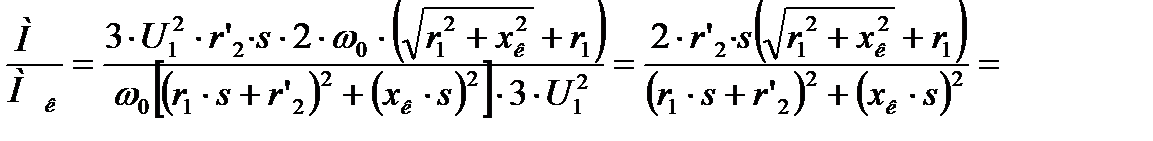
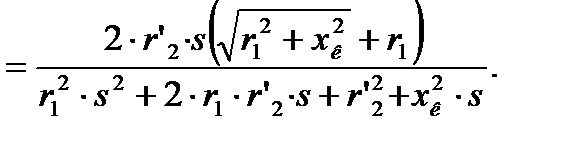
разделим числитель и знаменатель на

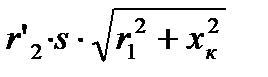
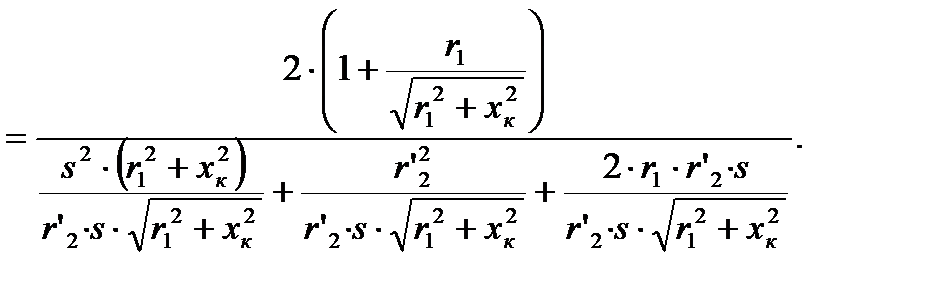
введём обозначение

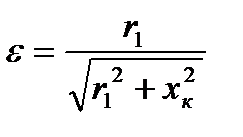
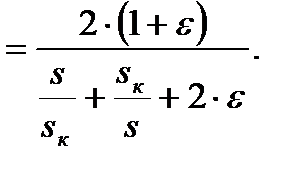
откуда

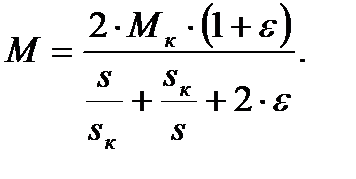(4.18)

Полученное выражение представляет собой уточненное урав­нение механической характеристики асинхронного двигателя. Как уже говорилось, для мощных асинхронных двигателей можно пренебречь величиной r₁ тогда ε = 0. Упрощенное уравнение ме­ханической характеристики:

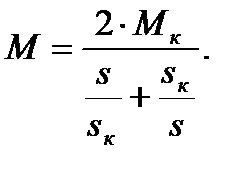(4.19)

Из курса «Электрические машины» известно, что r₁ 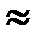r`₂. Следовательно, можно принять ε 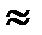s_к. Тогда уравнение механической характеристики будет иметь вид:

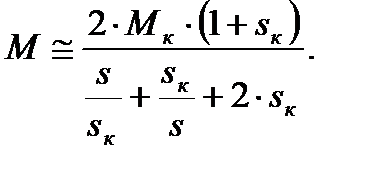(4.20)

Таким образом, для расчета механической характеристики требуются значения только М_к и s_к которые приводятся в пас­порте двигателя. Задаваясь s в требуемых пределах, можно по­лучить график механической характеристики. Выражением (4.20) достаточно точно описывается механическая характеристика асинхронного двигателя с фазным ротором. В двигателях же с короткозамкнутым ротором имеет место вытеснение тока в стержнях ротора. Поэтому механическая характеристика, пост­роенная по этим выражениям, несколько отличается от действи­тельной, особенно на пусковой части, а рабочая часть - сов­падает. Выражение (5.10) обычно используют для качественного анализа механической характеристики.

Для определения s _к в выражении (4.20) принимают s = s_н, М = М_н отношение 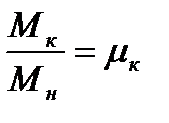- кратность критического момента:

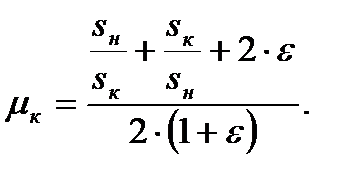
Примем ε = s_к. Тогда это выражение можно записать так:

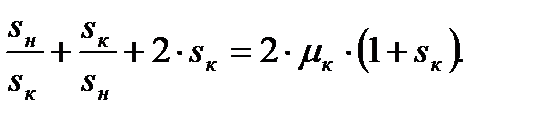(4.21)

Решим его относительно s_к:

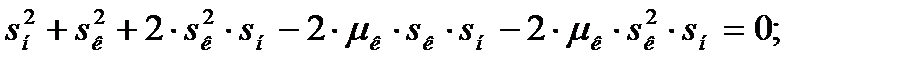
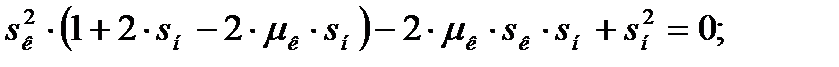
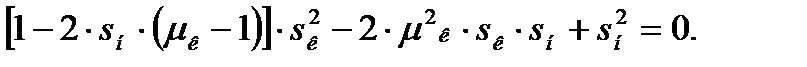(4.22)

Получим неприведенное полное квадратное уравнение. Решим его относительно s_к:

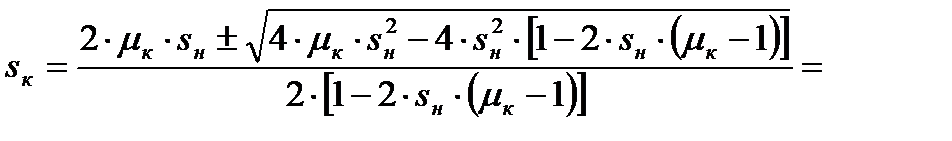
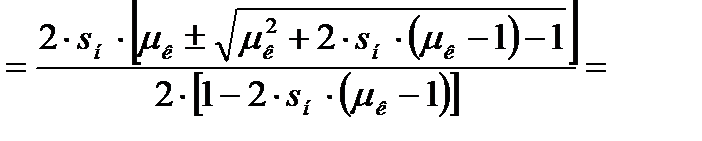
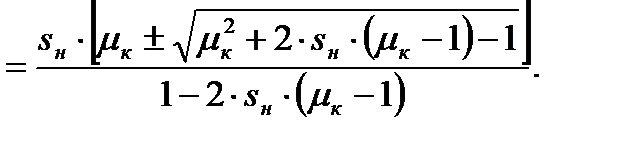(4.23)

Значение 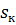при знаке «минус» перед корнем не имеет

физического смысла. Таким образом:

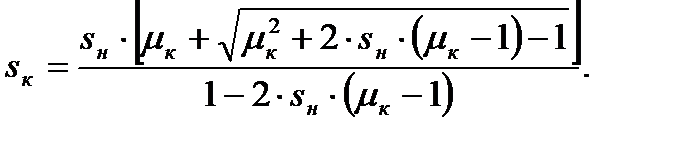(4.24)

При r₁ 0 получим упрощённое выражение:

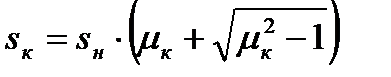. (4.25)

Необходимо отметить, что выражение (4.24) справедливо для двигателей мощностью более 20 кВт. Для двигателей меньшей мощности при расчетах возникают существенные погрешности.

Для анализа механической характеристики асинхронного двигателя рассмотрим упрощенное выражение механической характеристики асинхронного двигателя (4.26):

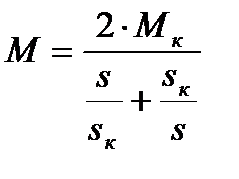. (4.26)

При изменении скольжения двигателя от 0 до (1.2…1.5)s и на рабочей ветви характеристики отношение 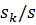больше 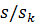в 8…10 раз. Поэтому пренебрегаем слагаемым 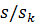в знаменателе этой формулы. Выражение механической характеристики запишем в виде:

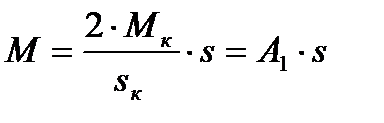. (4.27)

где 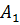- постоянный коэффициент, 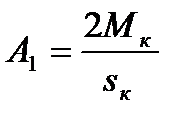. Это есть уравне­ние прямой линии. Значит, рабочая часть механической харак­теристики в рассматриваемых пределах линейна. Ближе к крити­ческомy моменту (после М > 0,7... 0,75 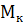) характеристика ста­новится нелинейной.

При 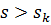к отношение s/ /s, поэтому пренебрегаем вторым слагаемым в знаменателе, а уравнение механической характери­стики примет вид:

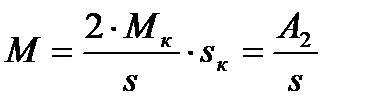. (4.28)

Это выражение - уравнение гиперболы, значит, пусковая ветвь механической характеристики нелинейная.

4.3. Построение естественных механической и

электромеханической характеристик асинхронного двигателя

по каталожным данным

Характеристика асинхронного двигателя естественна при

U_дв = U_н, отсутствии добавочного сопротивления в цепи ротора и статора и при частоте источника питания, равной номинальной

частоте двигателя.

Естественную механическую характеристику по каталожным данным строят при расчетах переходных процессов электропри­водa, определении: частоты вращения регулируемого двигателя, т.е. в тех случаях, когда нужно точно знать частоту вращения и момент [18].

Исходные данные берут из таблички на щитке двигателя или из каталога (5): номинальная мощность двигателя Р_н, кВт; номинальная частота вращения n_н. 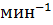, или значение номинального скольжения s_н (обычно в процентах); кратность критического момента М_к/М_н, для двигателей серии 4А ее обозначают μ_к; кратность пускового момента М_п/М_н обозначают μ_п; кратность минимального момента М_min/М_н - μ_min; критическое скольжение –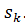

Естественную механическую характеристику АД строят по пяти точкам с соответствующими координатами:

Первая точка - синхронная угловая скорость ω_о = 2πf/р или ω_о = πn_о/30 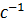, где f - частота питающей сети; n_о = 60f/р; p – число пар полюсов (определяется из типоразмера электродвигателя). В каталожных данных при f = 50 Гц синхронная частота вращения двигателя 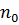= 3000, 1500, 1000, 750, 600, 500 и т.д. . Момент двигателя при ω_о равен нулю, т.е. эта точка лежит на оси ординат – частоты вращения;

Вторая точка – номинальные: частота вращения ω_н = πn_н/30 или 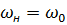(1- s_н), 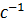и момент М_н = Р_н • 10^-3/ ω_н, Н•м.

Третья точка – критические: момент 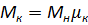и угловая скорость ω_к = ω_о(1 - s_к).

Если значение критического скольжения не приводится в справочной литературе, его определяют по формуле:

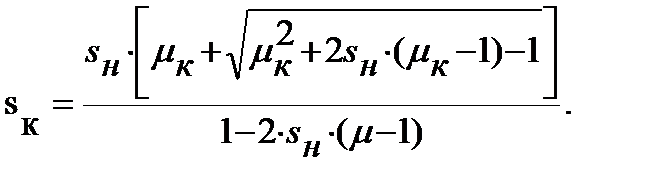
Четвертая точка – минимальные: момент М_м = М_н 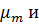скорость

ω_м = ω_о(1 - s_м), s_m= 6/7 для всех двигателей:

Пятая точка - пусковой момент М_п = М_н 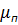, ω_о = 0.

Для более точного построения механической характеристики в области критического скольжения необходимо взять несколько промежуточных точек и определить значения момента по (4.20).

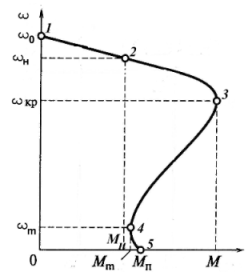
Рис. 4.3. Построение естественной механической характеристики

асинхронного двигателя.

Соединив плавной линией рассчитанные точки, получим график механической характеристики асинхронного двигателя (рис.4.3). На этой же рисунке пунктиром приведен график ме­ханической характеристики, построенной по уравнению (4.19).

Естественная электромеханическая характеристика асинхрон­ного двигателя I = f(ω) нужна при построении нагрузочных диаг­рамм для проверки двигателя на нагрев.

Рис.4.4. Построение естественной электромеханической

характеристики асинхронного двигателя.

Исходные данные можно взять из таблички двигателя и каталога: номинальная мощность двигателя Р_н, кВт; номинальное линейное напряжение двигателя U_н, B; номинальные коэффициенты: полезного действия η_н и мощности cosφ; кратность пускового тока 1_п; номинальное и критическое скольжение s_н, s_к. Естественную электромеханическую характеристику строят по четырем характерным точкам:

Первая точка имеет координаты :синхронная угловая скорость

ω_о = 2πf/р или ω_о = πn_о/30 и ток статора, соответствующий ω_о (ток намагничивания) :

I_c = I _н(sinφ_н - cosφ_н/2 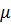_к), (4.30)

где 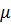_к - кратность критического момента ;

Вторая точка соответствует номинальным значениям:

I_н = P_н • 10³/( 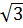• U_н • η_н • cosφ_н); ω_{н =} ω_о(1 - s_н);

Третья точка соответствует критическому скольжению дви­гателя:

ω_{к =} ω_о(1 - s_к); I_к = (0,7…0,8)I_пуск

Четвертая точка - пусковая: I_пуск = I_н • i_п; ω = 0

Соединив полученные точки плавной линией, получим график электромеханической характеристики. Обычно ее строят на одном графике с механической (рис.4.4).

4.4. Искусственные механические характеристики

асинхронного двигателя

Асинхронные двигатели, применяемые в сельскохозяйственном производстве, редко работают на естественной механической характеристике. Это вызвано несколькими причинами. Во-первых, при включении двигателей в сеть возникают большие пусковые токи, которые вызывают понижение напряжения на зажимах электродвигателей. Во-вторых, для выполнения требований технологии к электроприводу применяют регулировки или поддержание на заданном уровне координат двигателя (ω, М, I, P). Например, в обкаточных стендах или установках вентиляции помещений можно применять регулировки частоты вращения путем изменения напряжения, частоты и сопротивления в цепи ротора. Таким образом, асинхронные двигатели в рассмотренных случаях работают на искусственных характеристиках, когда U_дв ≠ U_н или r_доб, х_доб ≠ 0 или f_сети ≠ f_ном

4.5. Влияние изменения напряжения сети на

характеристики АД

Напряжение на обмотке статора изменяют с целью ограничения пусковых токов или регулирования скорости асинх­ронного двигателя. Напряжение регулируют с помощью авто­трансформатора, синхронного генератора или специальными полупроводниковыми

регуляторами напряжения.

Из уравнения механической характеристики (4.10) следует, что для любой частоты вращения асинхронного двигателя при постоянст­ве r₁, r₂' и х_к момент двигателя пропорционален квадрату напряжения:

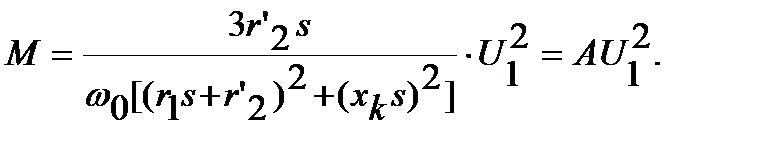
Таким образом, по естественной механической характеристи­ке, построенной при U_н , можно легко построить искусственную для напряжения U₁ < U_н:

М_иск/М_е = U₁²/U₁²_ном (4.33)

отсюда

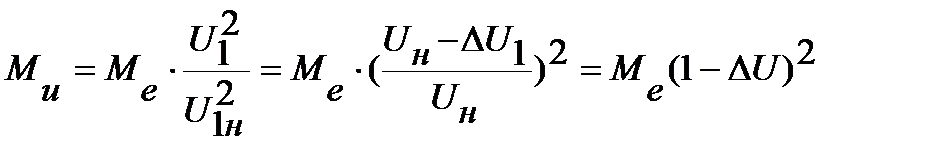
, (4.34)

где ΔU - относительное значение снижения напряжения на зажи­мах двигателя, ΔU = ΔU₁ /U_н .

Синхронная частота вращения ω_о и критическое скольжение s_к от напряжения не зависят, поэтому остаются постоянными при изменении напряжения.

Порядок построения искусственной механической характеристики при изменении напряжения следующий: по паспортным данным двигателя строим естественную механическую характеристику; определяем относительное значение снижения ΔU₁; задаемся значением частоты вращения ω₁ и для нее на естественной характеристике определяем М_1е; определяем момент М_1и при понижения напряжения по выражению (4.34); задаемся значением ω₂ и рассчитываем М_2и и т.д. Соединяем расчетные точки и получаем график механической характеристики при пониженном на ΔU напряжении (рис.4.5).

На практике чаще приходится рассчитывать не всю характе­ристику, а только номинальный пусковой и критический момен­ты. Так, для проверки двигателя по перегрузочной способности необходимо определить момент М_к при заданном или расчетном снижении напряжения. С этой целью критический момент, соответствующий номинальному напряжению пересчитывают к заданному (сниженному) значению напряжения и сравнивают с максимальным

рабочим:

М_к(1 - ΔU)² > M_cmax

Например, если М_к = 10 Н м, максимальный момент нагрузки

М_смах = 7 Н м, то при работе на естественной характеристике 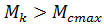; двигатель не "опрокинется". Если в сети произошло понижение напряжения на 20% из-за пуска рядом работающего мощного двигателя, то

М_к < М_смах, т.к. М_к(1 - ΔU)²=10(1 - 0,2)² = 10 0,64 = 6,4 Н м

Следовательно, асинхронный двигатель «опрокинется» (остано­вится). Такие же проверочные расчеты проводят при пуске.

Электромеханическая характеристика асинхронного двигателя (4.4) зависит от напряжения в первой степени. Следовательно, ток изменяется пропорционально напряжению.

I_и = I_е(1 - ΔU₁). (4.35)

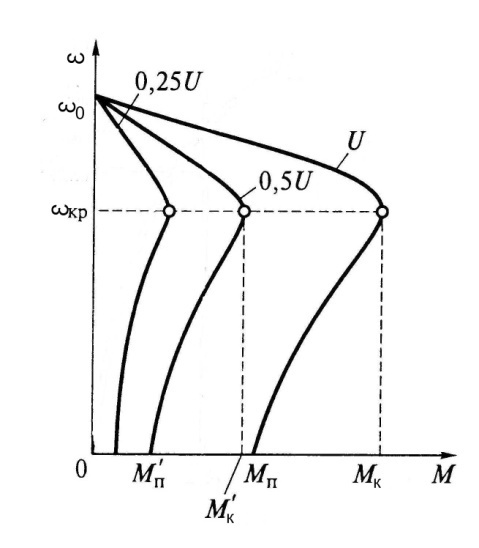
Рис. 4.5. Механические характеристики асинхронного двигателя при

понижении напряжения на статоре.

4.6. Влияние на характеристики асинхронного двигателя

добавочных активного и индуктивного сопротивления в цепи

статора

Добавочное активное или индуктивное сопротивление включа­ют в цепь статора для ограничения пусковых токов асинхронных двигателей [4]. Выясним поведение механической и электромехани­ческой характеристик асинхронного двигателя. При введении r_доб и х_доб в цепь статора синхронная скорость не изменяется, а критическое скольжение и критический момент уменьшаются:

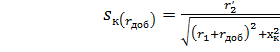; (4.36)

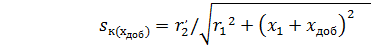; (4.37)

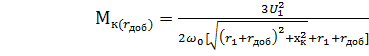; (4.38)

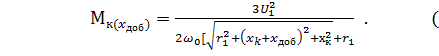4.39)
Пусковой момент определим из уравнения (4.10) при s = 1:

;

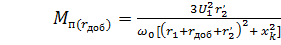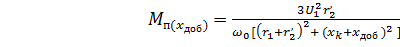. (4.40)

Следовательно, пусковой момент двигателя при введении в цепь

статора добавочного сопротивления снижается. Это явление необходимо учитывать при эксплуатации электроприводов различных технологических линий, отдельных машин и механизмов. При повышеннй нагрузке электродвигатель с включенными в цепи статора добавочными сопротивлениями может не запуститься, От этого может пострадать вся технологическая цепочка производства.

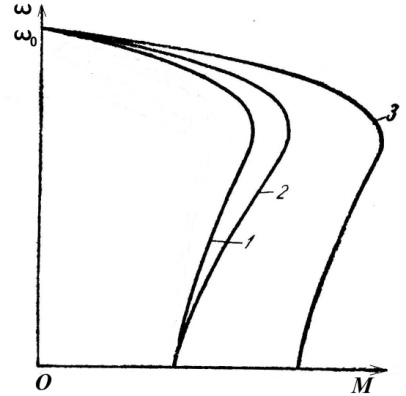
Рис.4.6. Механические характеристики асинхронного двигателя при введении в цепь статора добавочных сопротивлений: 1- активного, 2- индуктивного, 3 – естественная характеристика..

Промежуто­чные точки искусственной характеристики можно определить по формуле (4.20), подставляя значения s_ки и М_ки (рис.4.6).Для построения искусственной электромеханической характе­ристики при введении добавочного сопротивления запишем выра­жение механической характеристики (4.10):

М = 3∙I’_2е ∙ r’₂ / ω_o ∙ s; (4.41 )

пусть I₂ ≈ I_стат; тогда для любой постоянной скорости ω или s

М_е = I_е²∙А; М_и = I_и²∙А (4.42 )

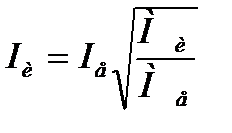где A = 3r₂'/ ω_os, откуда

Значит, для построения искусственной электромеханической характеристики необходимо иметь графики М_е, М_и, I_е. Задаваясь значением скорости, определим М_е, М_и и I_е, а затем по выражению (4.42) определим I_и.

4.7. Включение добавочного активного сопротивления в цепь

ротора

Добавочное активное сопротивление в цепь ротора асинхрон­ного двигателя включают для ограничения пусковых токов и ре­гулирования частоты вращения. Синхронная угловая скорость ω_о не изменяется, критическое скольжение s_к растет, так как увеличивается сопротивление ротора в соответствии с формулой (4.12.):

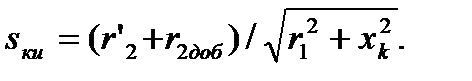
Значение критического момента М_к не изменяется, так как оно не зависит от r₂

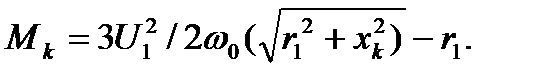(4.43)

Пусковой момент двигателя изменяется: вначале возрастает и при

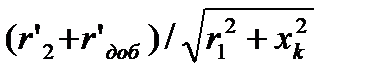
достигает величины критического момента (М_п = М_к). Дальнейшее увеличение добавочного сопротивления приводит к снижению пускового момента.

Определим соотношение скольжения двигателя при работе на естественной и искусственной характеристиках. Момент двига­теля на естественной характеристике:

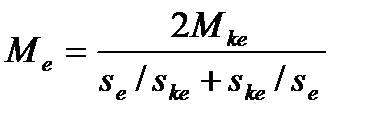
на искусственной характеристике:

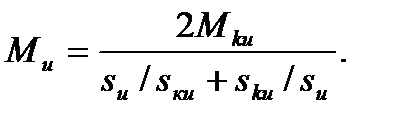
Приравниваем М_е и М_и, учитывая, что М_ке, = М_ки:

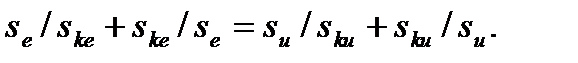
Обозначим: s_е /s_ке = y; s_и/s_ки = z. Тогда последнее уравнение

можно записать в виде

y +1/y = z +1/z.

Решим это уравнение:

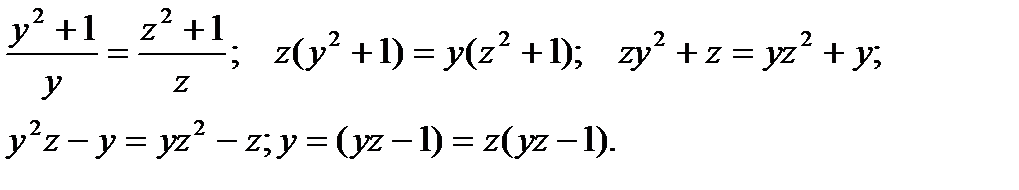
Уравнение имеет смысл при y = z. При yz = 1, y = 1/z или 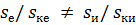, что не имеет физического смысла, так как 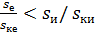. Таким образом при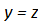

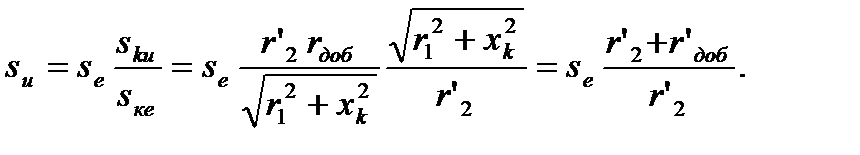
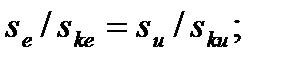
(4.44)

Для построения искусственной механической характеристики сначала необходимо построить естественную. Затем задаваясь значением момента М₁, определить по графику s_е1 и рассчитать s_и1:

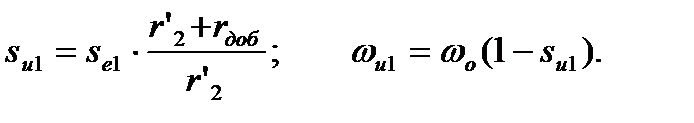
На практике достаточно взять значение момента двигателя от нуля до М_к (четыре-пять точек) и построить искусственную характеристику (рис.4.7). Электромеханическую характеристику рассчитываем по выражению, как для случая с добавочным активным сопротивлением в цепи статора.

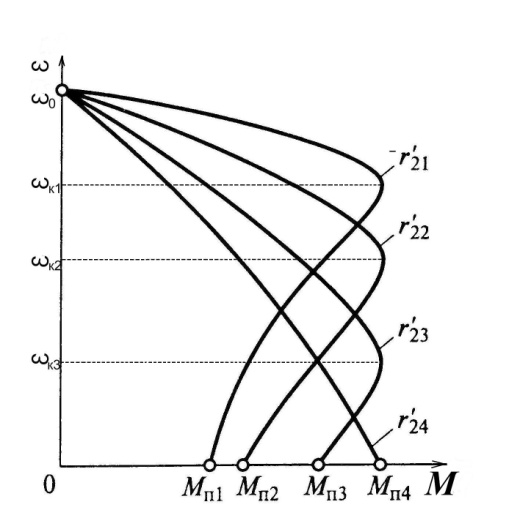
Рис. 4.7. Механические и электромеханические характеристики

асинхронного двигателя при введении добавочного резистора

в цепь ротора.

4.8. Влияние изменения частоты тока питающей сети

на работу АД
Изменение частоты питающей сети наблюдается при значительных колебаниях нагрузки в сетях с источником электроснабжения ограниченной мощности (при питании от резервной электростанции). В приводах частоту тока сети изменяют с целью регулирования частоты вращения или поддержания ее на заданном уровне [19]. При изменении частоты тока сети двигатель переходит на искусственную механическую характеристику. Частота вращения поля статора при изменении частоты от 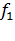до :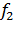

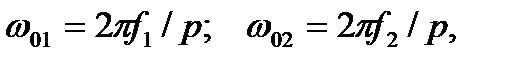(4.48)
отсюда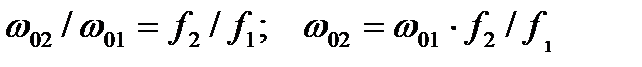

Синхронная частота вращения изменяется прямо

пропорционально изменению частоты сети. Определим характер изменения критического момента и критического скольжения. Для простоты пренебрегаем значением активного сопротивления статора .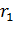
Тогда выражение (4.14) будет иметь вид:
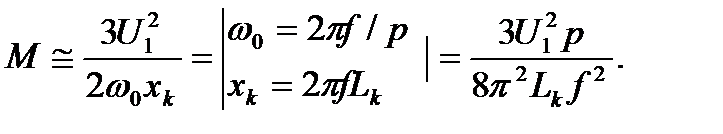(4.49)
Значение критического момента изменяется обратно пропорционально квадрату частоты. Для частот 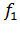и 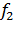, взяв соответственно отношение 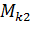и 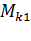, получим:
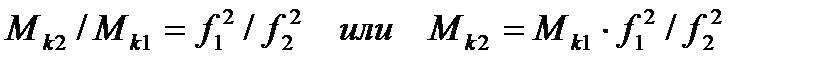. (4.50)
Для критического момента асинхронного двигателя при
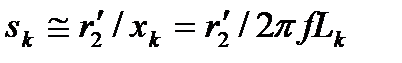. (4.51)
т.е. значение критического скольжения изменяется обратно пропорционально частоте. Пересчитать скольжение с одной частоты на другую можно, если взять отношение 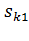и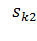
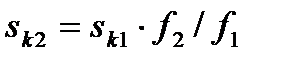. (4.52)

Значение изменения частоты вращения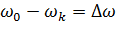

для разных частот тока:
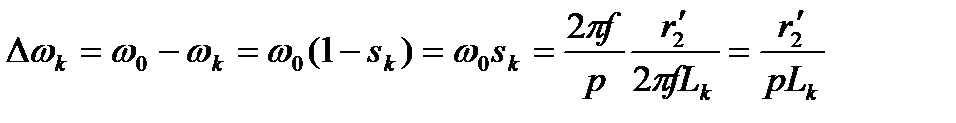. (4.53)

Если пренебречь изменением и в двигателе при

изменении частоты, то 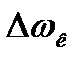будет иметь постоянное значение. Искусственные механические характеристики АД строят по выражению (4.19) или (4.20), для которых определяют 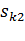и 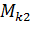. Задавшись значением s от 1 до нуля, рассчитывают искусственную механическую характеристику (рис.4.8).

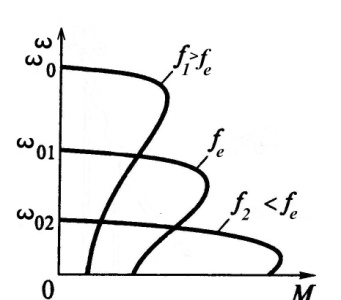
Рис. 4.8. Механические характеристики АД при изменении частоты.
4.9. Тормозные режимы асинхронных двигателей
Асинхронные двигатели, как и машины постоянного тока, обратимы и могут преобразовывать электрическую энергию в механическую (двигательный режим) и наоборот преобразовывать механическую энергию в электрическую (генераторный режим). Режим генераторного (рекуперативного) торможения происходит с отдачей энергии в сеть. Он возможен при частоте вращения ротора асинхронного двигателя выше синхронной ( > ).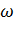
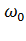Скольжение s = ( 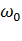- 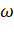)/ 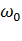< 0 отрицательно, следовательно, в выражении момента двигателя знак изменяется:

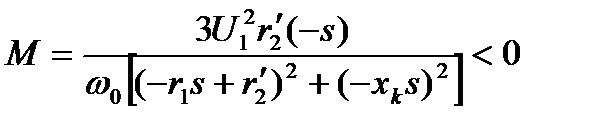. (4.54)
Рассмотрим особенности этого режима:
1) критическое скольжение не изменяется по значению, но меняется по знаку:
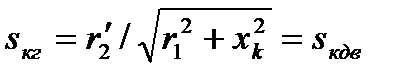. (4.55)

2) критический момент ( 4.14 ) будет больше критического момента 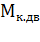в двигательном режиме:

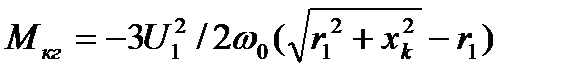. (4.56)
З) в двигательном режиме активная мощность

(из схемы замещения)
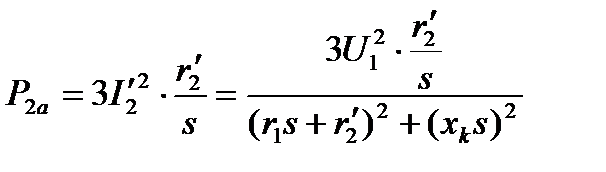. (4.57)

При любом s > 0 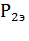> 0 . Активная мощность потребляется из сети и преобразуется в механическую.
При рекуперативном торможения при s < 0
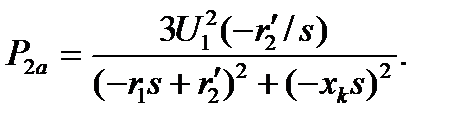(4.58)

Активная мощность изменяет свой знак. Механическая энергия, подведенная с вала рабочей машины, преобразуется в электрическую и отдается в сеть за вычетом потерь в электродвигателе.
Выясним характер изменения реактивной мощности:
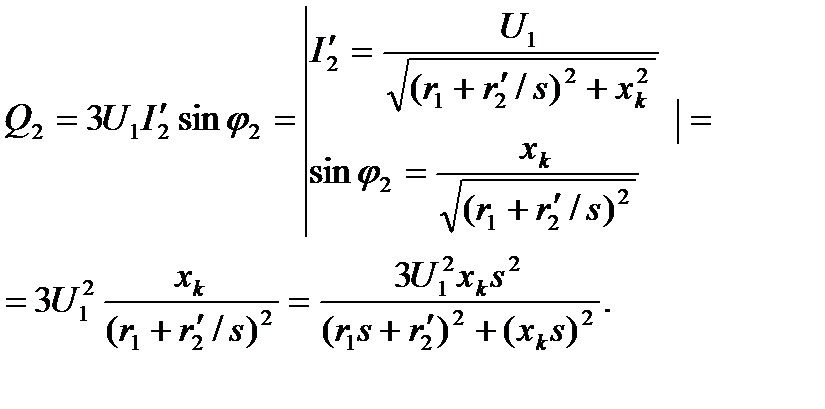(4.59)

При любом значении скольжения знак не изменяется. В режиме рекуперативного торможения реактивная мощность создает необходимое магнитное поле статора для возбуждения асинхронного

двигателя.

Механическую характеристику асинхронного двигателя строят по выражению ( 4.9). Характеристика располагается в четвертом или втором квадранте системы координат (рис.4.2) .

Рекуперативное торможение возможно в следующих случаях:

1) при работе с активным моментом подъемно-транспортных машин (кранов, кран-балок, лебедок и т.д.). Допустим, лебедка поднимает груз со скоростью v. Момент сопротивления, создаваемый грузом, равен (рис.4.10). В какой-то момент времени двигатель реверсируют. Следовательно, он перейдет на другую характеристику, из точки 1 в точку 2. Под действием сил инерции в первый момент времени ротор двигателя вращается с частотой вращения 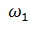(груз поднимается). Но так как 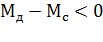, то и 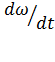< 0. Следовательно, груз тормозится и в точке 3 останавливается в верхнем положении, а затем под действием 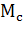и 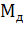начинает опускаться. В точке 4 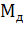= 0, но под действием груза электродвигатель разгоняется до точки 5,

где 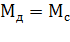. Груз опускается со скоростью 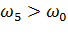, электрический двигатель находится в режиме рекуперативного торможения.

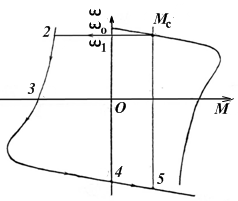
Рис. 4.10. Рекуперативное торможение асинхронного

двигателя при опускании груза.

Потенциальная энергия поднятого груза преобразуется в электрическую и отдается в сеть за вычетом потерь;

2) при переходе многоскоростного двигателя с высокой частоты вращения на низкую. Допустим, двухскоростной двигатель работает с моментом 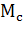в точке 1 на второй частоте вращения (рис.4.11). Если отключить вторую частоту вращения и включить первую, то электродвигатель перейдет в точку 2 характеристики первой частоты вращения. В этом случае 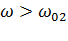, и двигатель находится в режиме рекуперативного торможения. Запасенная двигателем и рабочей машиной кинетическая энергия преобразуется в электрическую и отдается в сеть. А с уменьшением запаса кинетической энергии снижается и частота вращения, двигатель тормозится и переходит в точку З характеристики, где ;

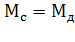3) при горячей обкатке ДВС после ремонта. Эта операция осуществляется в ремонтных мастерских и гаражах с помощью асинхронного двигателя с фазным ротором. В цепь ротора включают регулируемые резисторы. После окончания холодной обкатки выполняют горячую. С этой целью подают топливо в ДВС и запускают его. Постепенно увеличивают частоту вращения двигателя выше и асинхронный двигатель переводят в режим рекуперативного торможения. Регулируя значение сопротивления добавочного резистора в цепи ротора, изменяют загрузку ДВС и его частоту вращения [21].

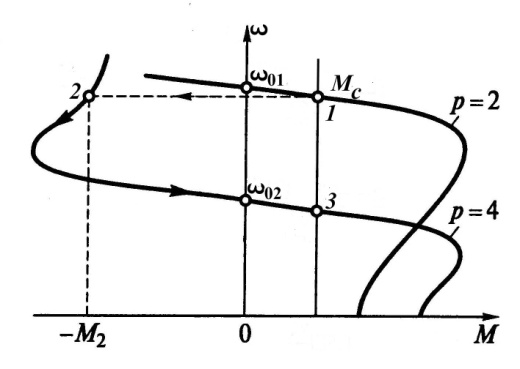
Рис. 4.11. Рекуперативное торможение асинхронного двигателя при

переключении частоты вращения.
Режим противовключения. Этот режим возникает в тех случаях, когда под действием внешних сил (активного момента рабочей машины или сил инерции) двигатель вращается в обратную сторону (против включения). Рассмотрим эти случаи более подробно:

1) асинхронный двигатель с фазным ротором приводит в движение лебедку, поднимающую груз (момент сопротивления ). Подъем идет со скоростью (рис.4.12). Вводим в цепь ротора добавочное активное сопротивление 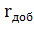, и двигатель переходит на искусственную механическую характеристику из точки 1 в точку 2. При введении сопротивления момент двигателя уменьшается до значения 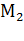, который меньше 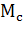. Двигатель тормозится. В точке З двигатель остановится, но > 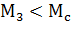и под действием груза двигатель начнет вращаться в обратную сторону. Таким образом, асинхронный двигатель перевели в тормозной режим противовключения. в точке 4 , груз будет опускаться с постоянной угловой скоростью

Рис.4.12. Режим противовключения асинхронного двигателя при

активном моменте.
2) асинхронный двигатель работает с рабочей машиной с угловой скоростью 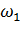. Предположим, что в какой-то момент времени мы осуществили реверс этого двигателя. Следовательно, он переходит на другую механическую характеристику (рис.4.13). Под действием сил инерции в первый момент времени частота вращения агрегата не изменяется, и двигатель переходит из точки 1 прямого вращения ротора в точку 2 обратного вращения.

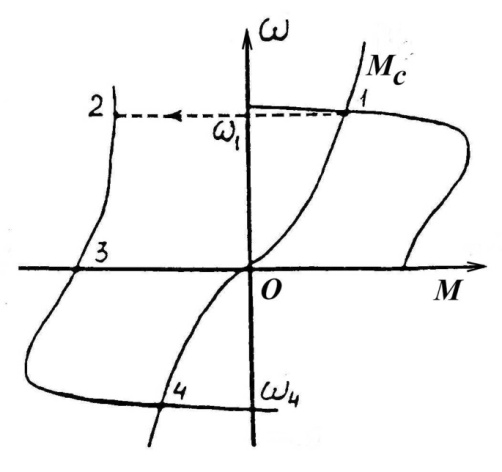
Рис.4.13. Реверсирование асинхронного двигателя

В точке 2 знаки момента и скорости разные, следовательно, режим работы - тормозной. При таком движущем моменте двигателя знак скорости должен быть отрицательным, а он положительный, значит, от точки 2 до точки З имеет место режим противовключения. Механические характеристики асинхронного двигателя в режиме противовключения располагаются во втором или в четвертом квадранте.
Рассмотрим особенности работы асинхронного двигателя в режиме противовключения. Прежде всего необходимо отметить, что если двигатель перевели в режим торможения, то преобразованная механическая мощность от рабочей машины или энергия сил инерции поступает в ротор, т.к. 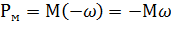для первого случая и 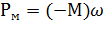= 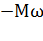- для второго. Электрическую мощность, поступающую из сети, можно определить по выражению
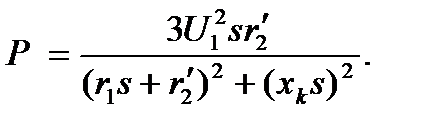(4.60)

В режиме противовключения s > 1, так как

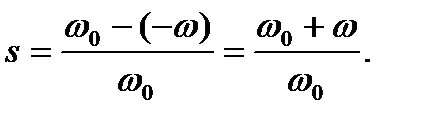
Знак электромагнитной мощности не изменяется. Это говорит о том, что и сетевая активная мощность идет в ротор. Таким образом, в ротор асинхронного двигателя по двум каналам поступает энергия, которая расходуется в его сопротивлениях. Значение суммарной мощности велико, и двигатель может быстро нагреться выше допустимой температуры. Для ограничения этого нагрева режим противовключения должен протекать кратковременно (при реверсе) или необходимы специальные меры: включение добавочных сопротивлений в цепь ротора, чтобы ограничить ток двигателя и вывести потери за

пределы обмоток двигателя.
Для определения характера изменения тока и момента двигателя в режиме противовключения представим электромагнитный момент двигателя в следующем виде:
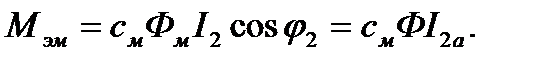(4.61)

где - постоянный коэффициент, определяемый конструкцией двигателя; 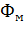- магнитный поток двигателя, пропорциональный напряжению сети; 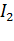- ток ротора; 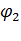– угол сдвига фаз тока и ЭДС ротора; 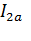- активная составляющая тока ротора.
Ток ротора

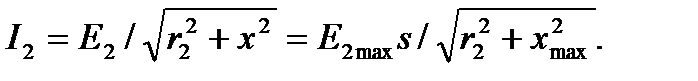(4.62)

где 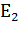– действующее значение ЭДС ротора; ;

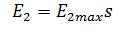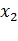- индуктивное сопротивление ротора,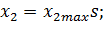

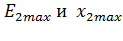- ЭДС и сопротивление при s = 1.
При работе в режиме противовключения s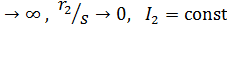

Таким образом, в режиме противовключения ток ротора и статора при s 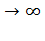стремятся к постоянному значению. Активная

составляющая тока ротора:
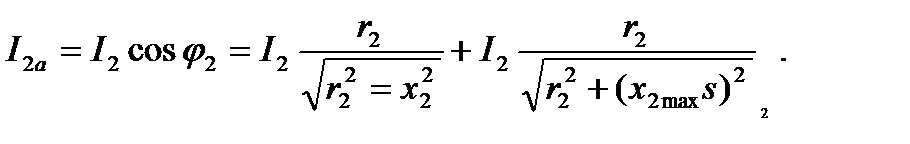(4.63)

При увеличении частоты вращения в режиме противовключения

(s 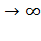) активная составляющая тока ротора и момент двигателя стремятся к нулю. Действительно, и по уравнению механической

характеристики
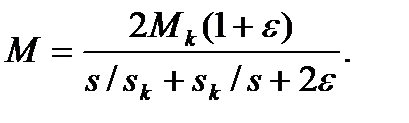(4.64)

при s 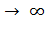электромагнитный момент будет уменьшаться до нуля.

Режим динамического торможения асинхронных двигателей осуществляется с независимым возбуждением и с самовозбуждением. В режиме динамического торможения с независимым возбуждением обмотку статора отключают от сети переменного тока и подают в нее постоянный ток. При этом обмотка статора создает постоянный магнитный поток, который пересекает вращающаяся обмотка ротора. Последняя включена на добавочное сопротивление или замкнута накоротко. В обмотке ротора наводится переменная ЭДС 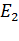и появляется ток 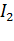, как и в обычном генераторе, только нагрузкой здесь служит сопротивление цепи ротора. Ток 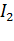взаимодействует с постоянным магнитным полем статора и создает тормозной момент. С уменьшением скорости снижаются ЭДС, ток и момент. При остановленном роторе тормозной момент равен нулю. Значение тока

ротора асинхронного двигателя
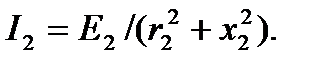(4.65)

где 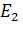– ЭДС ротора двигателя,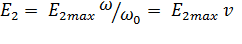

где v - относительное значение частоты вращения, ;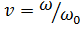

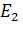- значение ЭДС ротора при синхронной частоте вращения .
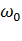Пренебрегая эффектом вытеснения тока в обмотке ротора, считаем постоянным значение его активного сопротивления .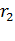
Индуктивное сопротивление
.
Принимаем постоянной индуктивность обмотки ротора 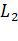. Частоту тока ротора 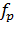представим в виде
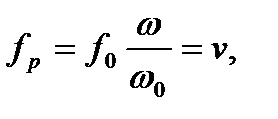(4.66)

где 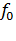- частота тока ротора при синхронной частоте вращения, для отечественных двигателей 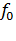= 50Гц. Индуктивное сопротивление

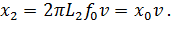
График изменения индуктивного сопротивления приведен на рис.4.14.
С учетом сказанного ток ротора можно записать в виде
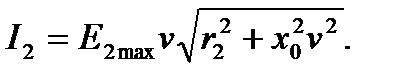(4.67)

Тормозной момент, как и двигательный, создается активной

составляющей тока :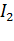
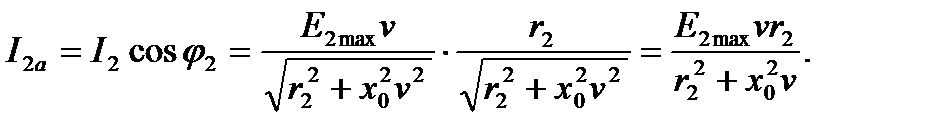(4.68)

При изменении частоты вращения ротора от нуля до бесконечности активная составляющая имеет максимум. Частота вращения, при

которой будет этот максимум:

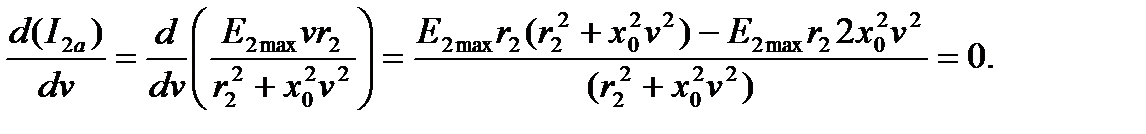
Дробь равна нулю, если числитель ее равен нулю, т.е.

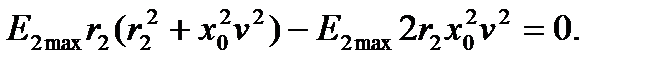
Решаем это уравнение относительно v
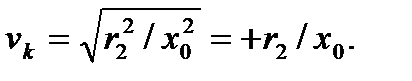v (4.69)

Рассмотрим график изменения сопротивлени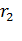й и 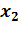на рис. 4.14.

Для анализа влияния значения сопротивления в цепи ротора асинхронного двигателя на тормозной момент необходимо выполнить построения, представленные на рис. 4.14.

Из подобных треугольников АОВ и СОД имеем соотношения:
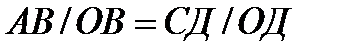или 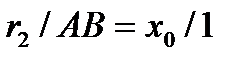откуда АВ =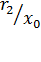

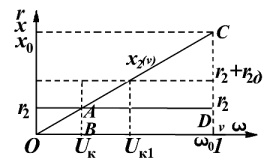
Рис. 4.14. График изменения сопротивлений в роторной цепи при

динамическом торможении асинхронного двигателя.
Следовательно, АВ = 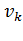. Из графика и выражения (4.70) видно, что максимальное значение динамического момента наступает при равенстве активного и индуктивного сопротивлений в цепи ротора. Необходимо отметить, что на синхронной частоте вращения значение индуктивного сопротивления значительно больше активного сопротивления обмоток ротора. Поэтому максимальное значение динамического момента находится на частоте вращения 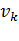, близкой к нулю. При включении добавочного сопротивления 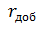в ротор значение частоты

вращения 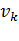увеличивается. Определим значение максимальной составляющей тока двигателя при :
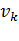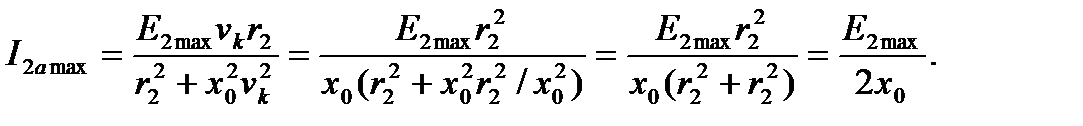(4.70)

Максимальное значение активной составляющей тока ротора зависит от ЭДС 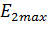, которое в свою очередь определяется для данного двигателя значением потока возбуждения (постоянного тока). График изменения активной составляющей тока ротора ( в другом масштабе это график динамического торможения) приведен на рис.4.15.

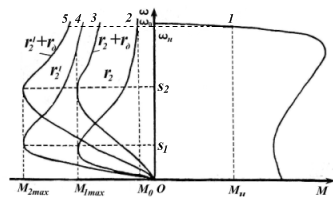
Рис.4.15. Механические характеристики асинхронного двигателя в

режиме динамического торможения.
Пусть двигатель работает с частотой вращения . Отключаем его от сети переменного тока и подаем в цепь статора постоянный ток 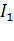. Возникает тормозной момент, и двигатель переходит в точку 2 характеристики динамического торможения. При снижении частоты вращения момент вначале растет, достигает 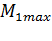, затем уменьшается до нуля. Выражения (4.69…4.71) дают представление о качественном изменении механических характеристик асинхронных двигателей. Этими выражениями трудно пользоваться для построения реальных механических характеристик, так как часто неизвестны параметры 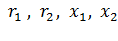. Для вывода расчетных формул механических характеристик в режиме динамического торможения постоянный ток, подаваемый в статор, заменяют эквивалентным переменным. И далее рассматривают работу как обычной асинхронной машины. Аналитическое выражение механической характеристики асинхронного двигателя в режиме динамического торможения имеет вид:
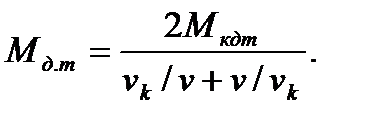(4.71)

где ; , - индуктивные сопротивления намагничивающего контура статора и обмотки ротора; - переменный ток статора, определяемый из равенства намагничивающих сил постоянного и переменного потоков = .

С учетом сопротивления обмотки статора относительное

значение критической частоты вращения можно записать в виде

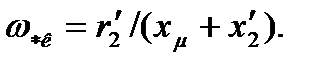(4.72)

Соотношение постоянных и переменных токов в зависимости от схемы нужно выбрать в табл.4.1

Таблица 4.1

Соотношения значений сопротивлений и токов для различных схем

динамического торможения АД.

Параметры	Схемы и значения параметров
Схемы включения обмоток
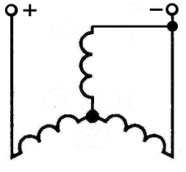
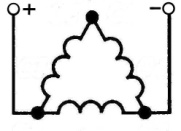
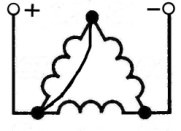
	2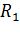
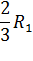
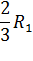
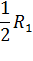
Соотношения токов 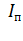=	1,23	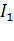1,41	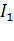2,12	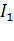2,45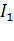

Таким образом, изменение сопротивления в цепи статора приводит к изменению максимальных значений тормозного момента, а изменение сопротивления в цепи ротора - к изменению скольжения.

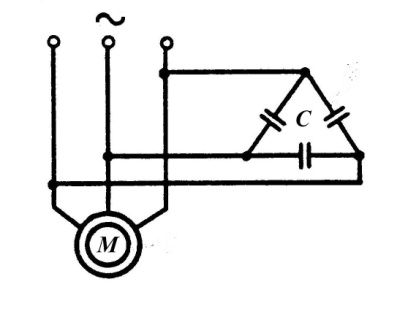
а б в

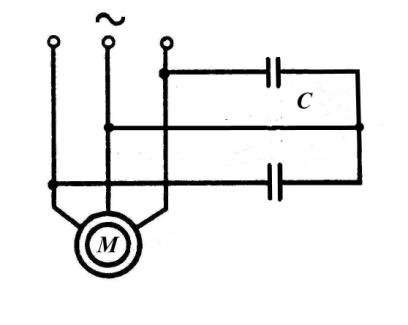
Рис.4.16. Схемы включения конденсаторов в режиме динамического торможения асинхронного двигателя с самовозбуждением.
Динамическое торможение с независимым возбуждением нашло применение в приводах, где требуются быстрая и точная остановка механизма, сокращение продолжительности переходного процесса в электроприводах. Оно имеет достоинства: потери а двигателе ниже, чем при противовключении; не требуется отключать двигатель при нулевой частоте вращения; обеспечивается точная остановка привода.

Динамическое торможение с самовозбуждением осуществляется с помощью конденсаторов. у работающего двигателя отключают от сети обмотку статора и подключают батарею конденсаторов по схеме (рис.4.16) [12]. Можно использовать бумажные и электролитические конденсаторы. Процесс самовозбуждения можно проследить по рис.4.17. Торможение при самовозбуждении основано на том, что после отключения АД от сети его электромагнитное поле затухает (исчезает не мгновенно) в течение некоторого, пусть и небольшого интервала времени. За счет энергии этого затухающего поля и использования специальных схем включения АД можно обеспечить его самовозбуждение и реализовать тормозной режим. На практике применение нашли так называемые конденсаторное и магнитное торможение АД. При конденсаторном торможении возбуждение АД осуществляется с помощью конденсаторов С, подключаемых к статору. Отметим, что конденсаторы могут подключаться к статору постоянно (глухое подключение) или с помощью дополнительного контактора, будучи при этом соединенными в схему треугольника или звезды.

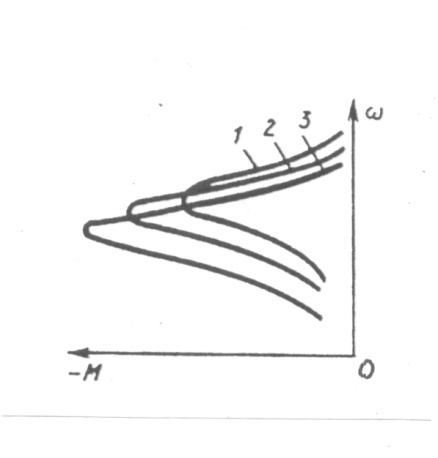
Рис.4.17. График изменения ЭДС и напряжения на конденсаторе

в зависимости от тока асинхронного двигателя.
Определяющий фактор, от которого зависят вид и расположение характеристик АД 1... 3 (см. рис.4.18, а значит, интенсивность торможения - емкость конденсаторов С (кривые 1… 3 соответствуют значениям 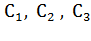). Чем она больше, тем больше будет максимум тормозного момента, а характеристики будут смещаться в область низких частот вращения АД.

Магнитное торможение реализуется после отключения статора двигателя от сети и замыкания с помощью контактов К его выводов накоротко (рис.4.19).

Рис.4.19. Схема магнитного торможения асинхронного двигателя.

За счет запасенной в двигателе электромагнитной энергии проходит самовозбуждение двигателя и на его валу создается тормозной момент. Особенностью такого торможения является быстротечность, определяемая небольшим временем затухания магнитного поля двигателя, однако возникающие при этом тормозные моменты достаточно велики и обеспечивают интенсивное торможение электропривода.

Тиристорные схемы существенно расширили практические возможности торможения АД, которые позволяют осуществлять как пуск двигателя, так и его торможение. Для обеспечения интенсивного торможения двигателя часто используется комбинированный способ, например динамическое торможение в сочетании с торможением коротким замыканием. Этот способ может быть реализован тиристорным устройством (см.рис.4.20) состоящим из двух пар встречно-параллельно включенных тиристоров VS1…VSб , служащих для подключения или отключения двигателя от источника питания, и дополнительного тиристора VS5 для торможения коротким замыканием обмоток статора.

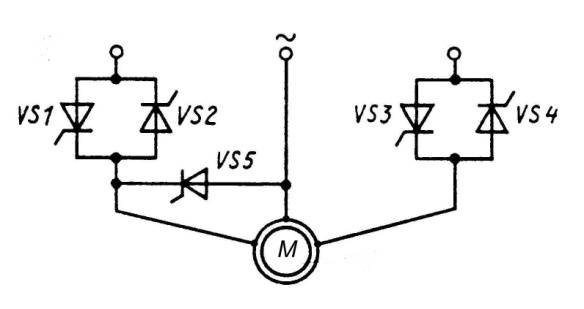
Рис.4.20. Схема тиристорного торможения асинхронного двигателя.

Торможение осуществляется следующим образом. После закрытия тиристоров и отключения двигателя от сети подается сигнал управления на тиристор VS1 , который замыкает накоротко две фазы статора. Когда интенсивность торможения коротким замыканием обмоток статора уменьшится, сигнал управления подается на тиристор VS1 который пропускает в цепь статора выпрямленный ток и тем самым обес-

обеспечивает режим динамического торможения. Серийные тиристорные пускорегулирующие устройства обеспечивают и другие варианты торможения АД, а также так называемый безударный его пуск, при котором снижаются броски электромагнитного момента.

4.10. Ограничение пусковых токов асинхронных

двигателей

При включении асинхронного двигателя в сеть возникает большой пусковой ток, превышающий номинальный в 5…7 раз и вызывающий в линии значительное падение напряжения, что может привести к остановке рядом работающих двигателей. Под действием пускового тока в двигателе возникают динамические усилия, повреждающие и разрушающие обмотку, нагружаются силовые трансформаторы и линия, что приводит и дополнительным потерям мощности ‚ ограничение пусковых токов особенно актуально для сельскохозяйственных установок из-за удаленности электродвигателей от источников питания и соизмеримости мощности трансформаторов и пусковой мощности электродвигателей. Частые пуски нагревают обмотки двигателя.
Ограничить пусковые токи можно несколькими способами: включением добавочного активного или индуктивного сопротивления в цепь статора; включением добавочного активного или индуктивного сопротивления в цепь ротора; переключением обмотки статора на период пуска с «треугольника» на «звезду»; понижением напряжения на статоре. Схемы снижения пусковых токов путем переключения обмоток со «звезды» на «треугольник» (рис.4.21) можно рекомендовать для электродвигателей, фазные обмотки которых рассчитаны на линейное напряжение. Это относится к электроприводам прессгрануляторов, мощных дробилок и т.п.). В сети с напряжением 380 В необходимо применять двигатели рассчитанные на напряжение 660/380 В. При напряжении сети 380 В у двигателя должно быть напряжение 380/220 В.

Рассмотрим соотношение пусковых токов двигателя при соединении в «звезду»:
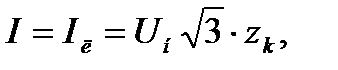(4.73)

где 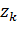- полное сопротивление обмотки статора при включении.

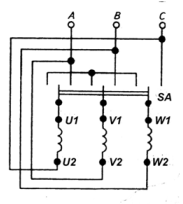
Рис. 4.21. Схема переключения обмоток статора асинхронного

двигателя со «звезды» на «треугольник».

Пусковые токи двигателя при включении обмоток в «треугольник»:

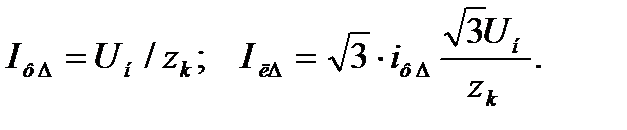
Отношение токов:
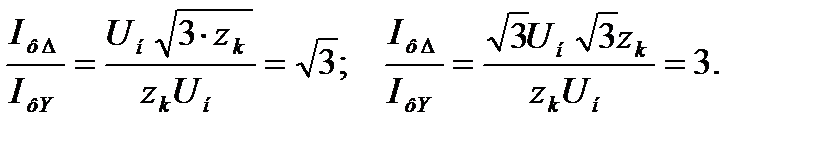(4.74)

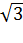Таким образом, при включении обмоток двигателя в «звезду» фазный ток уменьшается в раз, а линейный - в три раза. При понижении напряжения на фазе в 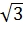раз момент двигателя уменьшается в три раза.

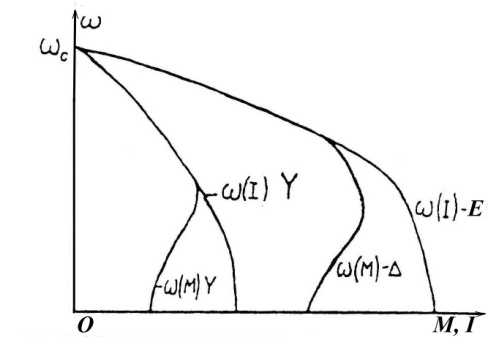
Рис.4.22. Характеристики асинхронного двигателя при

переключении обмоток статора со «звезды» на «треугольник».

Механические и электромеханические характеристики при пуске двигателя этим способом приведены на рис.4.22. Пусковые токи асинхронных двигателей можно ограничить понижением напряжения на статоре.
Пусковой ток асинхронного двигателя при номинальном напряжении питания равен:

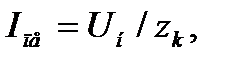
где 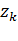- сопротивление фазы двигателя в момент включения.
Для снижения пускового тока в а раз напряжение на статоре асинхронного двигателя необходимо снизить в это же число раз
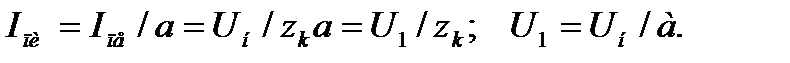(4.75)

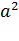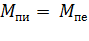Уменьшение напряжения на статоре вызывает снижение пускового момента двигателя в или (1 - 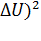. На рис.4.23 изображены механические и электромеханические характеристики асинхронного двигателя при снижении пускового тока а два раза. Значительное уменьшение пусковых моментов позволяет использовать данный способ в основном при пуске двигателей на холостом ходу с небольшим относительно 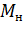, моментом трогания.

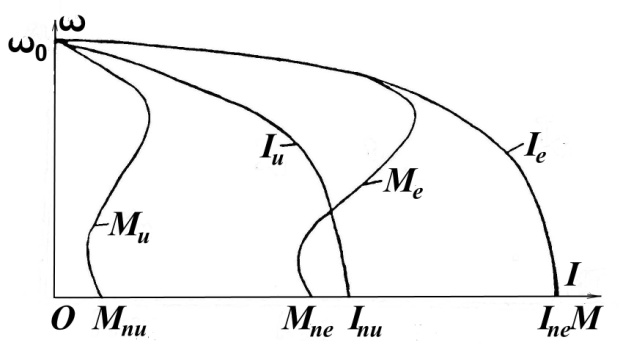
Рис.4.23. Характеристики асинхронного двигателя при понижении

напряжения.
В расчетах при выборе двигателя обязательна проверка на возможность пуска при понижении напряжения: .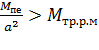
Ограничить пусковые токи асинхронных двигателей можно включением добавочного активного или индуктивного сопротивления в цепь статора [16].
Расчет значения добавочного активного 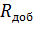или индуктивного 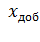сопротивления начинают с выбора необходимого пускового тока 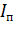и определения кратности снижения этого тока:
,
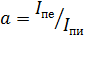где - пусковой ток двигателя при отсутствии сопротивления в

цепи статора, =
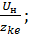
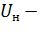номинальное фазное напряжение сети; сопротивление обмотки фазы статора; 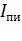- пусковой ток при введении добавочного сопротивления в цепь статора, 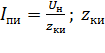- полное сопротивление цепи обмотки статора при введени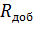и или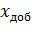
Подставим значения токов 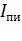и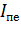

a = .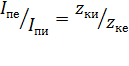

Для определения необходимого значения cтроят треугольник сопротивлений (рис.4.24).

Рассчитываем полное сопротивление обмотки двигателя:

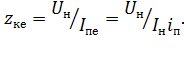
Затем активное сопротивление
,
где 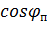- коэффициент мощности двигателя при пуске;

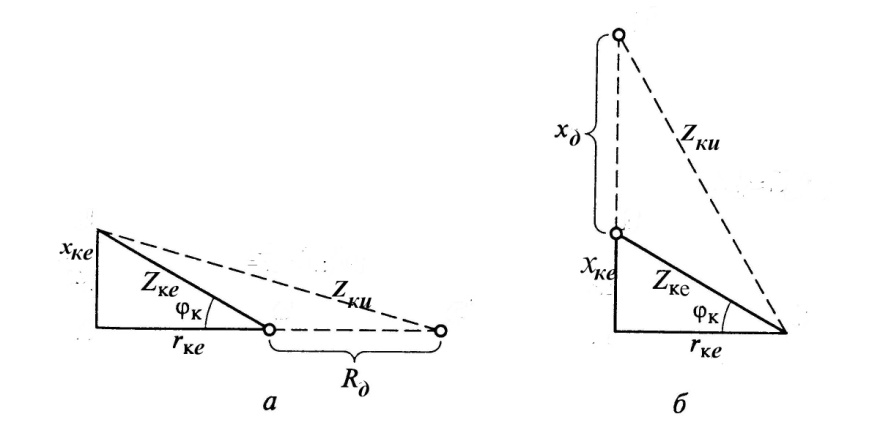
Рис.4.24. Треугольники пусковых сопротивлений при включении в цепь статора асинхронного двигателя: а – активного сопротивления;

б – индуктивного сопротивления.

индуктивное сопротивление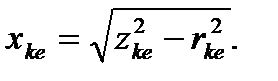

Из треугольника сопротивлений (рис.4.25, а) имеем
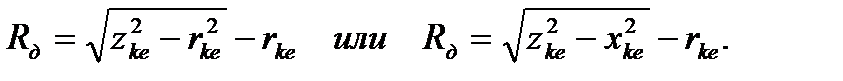(4.76)

Аналогично определяем значение добавочного индуктивного

сопротивления (рис.4.24, б ):
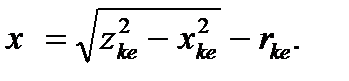(4.77)

Механические и электромеханические характеристики двигателя при введении добавочных сопротивлений рассмотрены ранее.
Пусковая диаграмма двигателя приведена на рис.4.25. Сопротивление 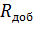или 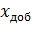отключают после разгона двигателя или в какой то момент времени, при котором скачок тока не превышает .
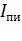Ограничение пусковых токов асинхронных двигателей возможно и включением добавочных резисторов в цепь ротора [4]. При пуске асинхронного двигателя с фазным ротором с замкнутыми накоротко кольцами пусковой момент равен (0,5... 1,5) 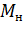, а ток статора и ротора превосходит номинальный в 5... 10 раз.

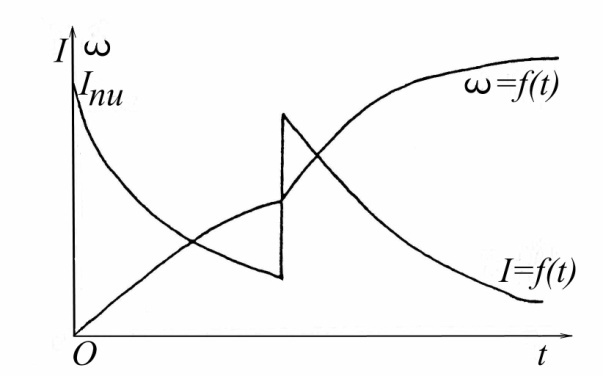
Рис.4.25. Диаграммы тока пуска асинхронного двигателя с

помощью резистора в цепи статора.

Введение в цепь ротора активных сопротивлений снижает токи двигателя и увеличивает пусковой момент до (см. рис.4.7). Схемы включения ступеней пусковых резисторов приведены на рис.4.2, 6.

Рис. 4.26. Схемы включения пусковых резисторов асинхронного

двигателя.

4.11. Расчет пусковых резисторов для асинхронных двигателей
Расчеты пусковых резисторов для асинхронных двигателей с фазным ротором аналогичны расчетам пусковых резисторов для шунтовых и сериесных двигателей [18]. При этом необходимо учесть, что на рабочей части механической характеристики асинхронного двигателя момент пропорционален току, поэтому расчеты ведут для моментов, а не для тока [4]. Значение максимального пускового момента ограничивается динамическими усилиями в обмотках и нагревом машины. В некоторых случаях этот момент ограничивается требованиями технологии. Расчет сопротивлений пусковых резисторов можно выполнить точными и приближенными методами аналитическим и графическим методом. Рассмотрим приближенный метод, который применяют при максимальных моментах переключения, не превышающих 0,7 Диаграмма пуска асинхронного двигателя в две ступени приведена на рис.4.28.

Аналитический метод. Если число ступеней m задано, то

кратность моментов переключения
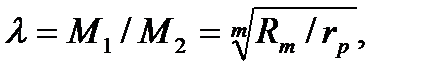(4.78)

где 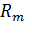- максимальное сопротивление роторной цепи в момент включения, 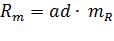; масштаб сопротивления

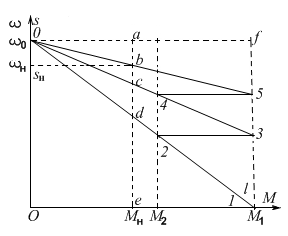
Рис.4.28. Пусковая диаграмма асинхронного двигателя. 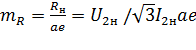, - сопротивление ротора, аb
После подстановки значени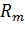й и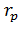
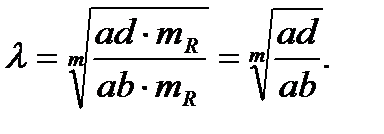(4.79)

Отрезок ab = , а размер отрезка определим из подобных

треугольников Oad и ofl:

аd/ao = lf/of;
отрезки аО = 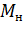; lf = 1; jf = 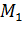, следовательно:
а d = ао lf / of = ; .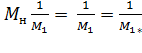

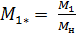Таким образом,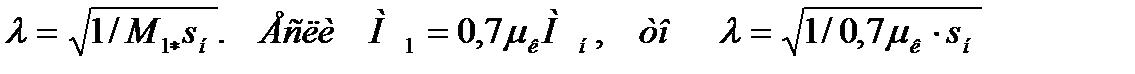

Значение 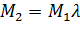должно быть больше , т.е. . По аналогии с машинами постоянного тока (глава 2 и 3)

определим сопротивление:
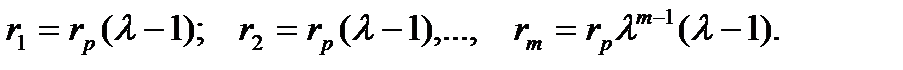(4.80)
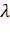Когда число ступеней не задано, принимаем значения моментов переключения и , затем определяем и число ступеней m:
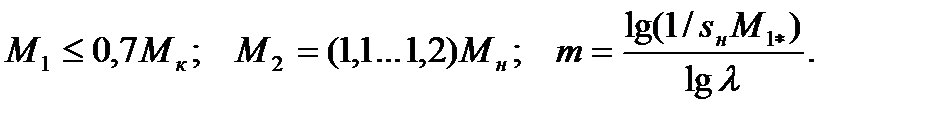(4.81)

Полученное число ступеней округляем до целого и уточняем значение 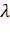. Далее расчет выполняем, как в первом случае.
Графический метод. Порядок построения пусковых

характеристик такой же, как и для машин постоянного тока параллельного возбуждения. Сначала по паспортным данным машины строим естественную механическую характеристику 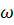= f(M) и задаемся моментами переключения 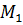и (рис.4.28). Строим пусковую характеристику: проводим линию 1 – 2 - 0 до пересечения в точке 2, затем 3 – 4 - 0 и т.д. до совпадения я точке 5 (момент )на естественной характеристике. На линии номинального момента определяем значения сопротивлений ступеней резисторов:
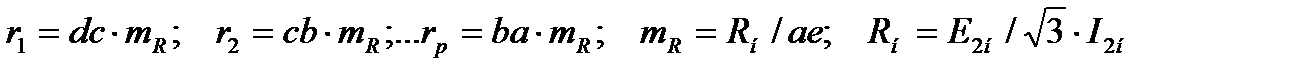(4.82)
где 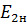, 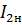- номинальные значения ЭДС и тока ротора.
Для проверки, необходимо определить сопротивление ротора и сравнить его с полученным графическим методом
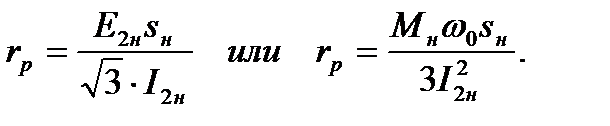(4.83)

4.12. Электроприводы с линейными электродвигателями
В настоящее время около 40-50% серийных электродвигателей эксплуатируется в производственных механизмах с поступательным или возвратно-поступательным движением рабочего органа. Для преобразования вращательного движения в поступательное используются разнообразные устройства: пневмо- и гидропередача, пара «винт - гайка»; кривошипно-шатунный механизм, шестерня и рейка, колесо и путевая структура в транспортных системах и др. Кроме того, в таких приводах, как правило, используются редукторы, являющиеся местом дополнительных потерь и отказов.
Линейные электродвигатели позволяют непосредственно осуществить поступательное движение без механического контакта между первичной (обычно статором) и вторичной (ротором) структурами, следовательно, исключить передаточный механизм. При этом значительно упрощается кинематическая схема, повышается надежность, точность управления, а сами линейные электродвигатели хорошо пристраиваются к исполнительному механизму, обладают технологичностью в производстве и меньшим расходом стали благодаря малоотходному раскрою.
На практике применяются линейные двигатели постоянного тока (в основном - шаговые), асинхронные (ЛАД), синхронные (ЛСД) и электромагнитные (ЛЭМД). Получают распространение линейные асинхронные двигатели в силу их конструктивной простоты, дешевизны, технологичности изготовления, надежности, разнообразия конструктивных решений. Конструктивно ЛАД выполняют цилиндрическими и плоскими.
На рис.4.29 показано устройство плоского ЛАД.

Рис.4.29. Устройство плоских линейных асинхронных двигателей:

1-индуктор с обмоткой (статор); 2- реактивная шина; 3- обратный магнитопровод; а – двухсторонний ЛАД; б – односторонний ЛАД; в – короткозамкнутая обмотка с обратным магнитопроводом.

Управление параметрами движения ЛАД осуществляют так же, как и обычным АД: изменением сопротивления реактивной шины, регулированием частоты и длительности включений. ЛАД применяются в конвейрах, ворошителях бункеров-питателей сыпучих грузов, транспортных средствах, ручном инструменте и т.п. Важным преимуществом ЛАД состоит в высоком значении .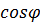

4.13. Способ маркировки выводов обмоток трехфазных

асинхронных двигателей

Для включения трехфазных электродвигателей в сеть на выводах их обмоток должна быть нанесена маркировка, пользуясь которой можно собрать схемы соединения обмоток «звездой» и «треугольником». В практике эксплуатации, особенно после ремонта, встречаются электродвигатели, у которых отсутствуют обозначения начал и концов фаз. Вследствие этого возникает необходимость в определении начал и концов фаз электродвигателей. В разное время были предложены методы определения начал и концов фаз трехфазных электродвигателей, которые применяются достаточно широко и сегодня: метод трансформации, метод подбора. У них есть существенные недостатки, связанные с необходимостью выполнять ряд переключений выводов фаз. Эти операции требуют значительных затрат времени.

Автором предложен более простой метод определения начал и концов фаз трехфазных электродвигателей, который заключается в следующем. Сначала известными методами с помощью контрольной лампы или вольтметра определяют попарную принадлежность выводов к каждой из трех фаз электродвигателя. Затем три фазы соединяют последовательно (в открытый треугольник), как показано на рис.4.30. Параллельно каждой фазе присоединяют вольтметры. Собранную таким образом электрическую цепь включают в сеть. Если фазы электродвигателя оказались включенными согласно: начало-конец-начало-конец-начало-конец, то вольтметры покажут одинаковые значения напряжения.

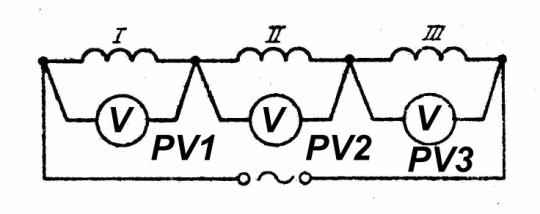
Рис.4.30. Схема соединения фаз трехфазного электродвигателя

в открытый треугольник.

Если одна из фаз оказалась включенной в открытый треугольник встречно по отношению к двум другим, то вольтметр, подключенный к ней, покажет большее напряжение по сравнению с показаниями двух других вольтметров.

Руководствуясь показаниями последних, можно сразу осуществить маркировку начал и концов фаз электродвигателя.

а б

Рис.4.31. Взаимное расположение магнитных потоков взаимной

индукции в статоре трехфазного электродвигателя при включении обмоток в открытый треугольник: а – согласном; б – встречном.

Существо процессов, происходящих при разметке выводов фаз электродвигателя описанным методом, заключается в следующем. Рассмотрим магнитную цепь трехфазного электродвигателя, которая представлена на рис.4.31, а при согласном включении фаз. Каждая из них создает магнитные потоки самоиндукции и взаимной индукции. На рис. 4.30 для удобства у каждой фазы изображено два потока взаимной индукции, сцепляющихся с соседними фазами. Магнитные потоки взаимной индукции из трех фаз направлены навстречу друг другу. Этим объясняется равенство напряжений на зажимах всех фаз. Уравнения, характеризующие значения напряжения на зажимах фаз, имеют вид:

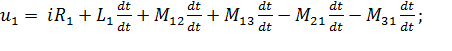(4.84)
;
.
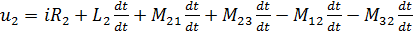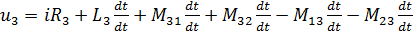В комплексной форме записи эти уравнения имеют вид:

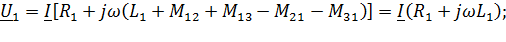
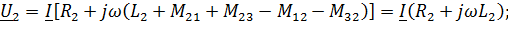(4.85)

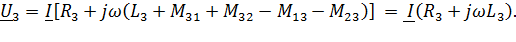
Так как конструкции фаз электродвигателя одинаковы и все входящие в уравнения (4.84) и (4.85) параметры соответственно равны

т.е. 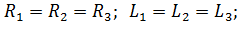то и

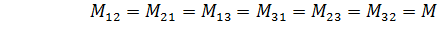
Поэтому

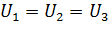
Векторная диаграмма для этого случая приведена на рис.4.31.

Случай встречного включения одной из фаз электродвигателя при соединении их в открытый треугольник представлен на рис.4.31, б. Из этлгл рисунка видно, что витки третьей фазы, включенной встречно двум другим, пронизываются четырьмя потоками взаимоиндукции 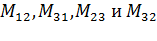, которые направлены в одну сторону.

Представленные примеры относятся к магнитным цепям, электромагнитные процессы в которых описывают при помощи понятий магнитодвижущей силы, магнитного потока и разности магнитных потенциалов. В завимости от исполнения магнитные цепи можно классифицировать по разным признакам.

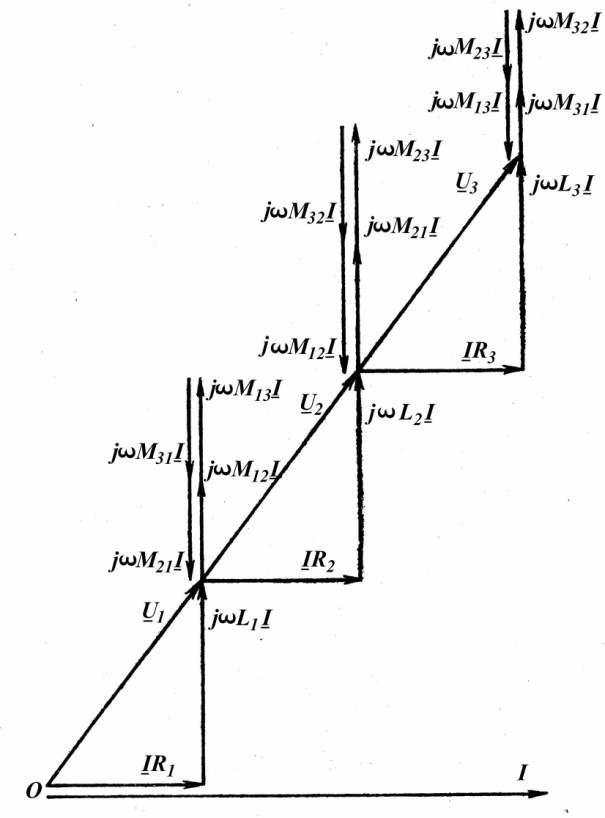
Рис.4.32. Векторная диаграмма для согласного включения фаз

двигателя при соединении в открытый треугольник.
Две другие фазы пронизываются потоками взаимной индукции в различных направлениях. Этим объясняется наличие большего значения напряжения на фазе, включенной встречно по отношению к двум другим. Уравнения, подтверждающие это положение имеют вид:

;

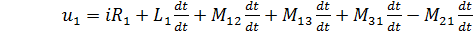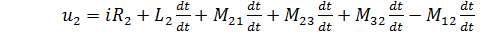(4.86);

.
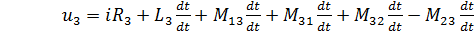Действительно, уравнение, определяющее значения напряжения на зажимах фазы, включенной встречно по отношению к другим, имеет на два слагаемых больше. В комплексной форме записи эти уравнения принимают вид:
= [

= [ ;

= [
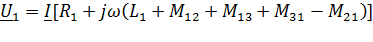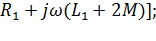
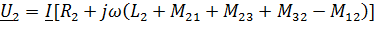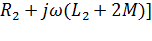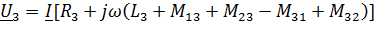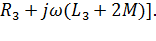
Таким образом, по векторной диаграмме, представленной на рис.4.33, видно, что вектор напряжения s w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 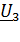(на зажимах фазы, включенной встречно) больше по сравнению с векторами .

Рис.4.33. Векторная диаграмма для встречного включения одной из

обмоток электродвигателя.

Большие различия в напряжениях на обмотках возникают при вынутом роторе. Новый способ маркировки выводов фаз трехфазных электродвигателей теоретически обоснован, прост в реализации и успешно применяется на практике и в учебном процессе.