Осевые моменты инерции твердого тела

Дата: 2025-06-02; Просмотры: 7

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Характер распределения массы тел относительно плоскости, оси или центра существенно влияет на движение этих тел (системы тел) и характеризуется соответствующим моментом инерции. Ограничимся рассмотрением моментов инерции относительно оси (рисунок 5.3).

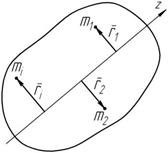Момент инерции тела относительно оси – это сумма произведений массы каждой точки тела на квадрат расстояния от оси до точки:

J = åm r2 , [J ]= éëкг × м2 ùû .

Рисунок 5.3

Для тонкостенного кольца (рисунок 5.4) рас-

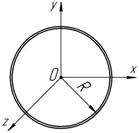стояние r i

есть величина постоянная равная R :

J = åm r2 = R2 åm

= mR2 .

Рисунок 5.4

Момент инерции любого тела можно представить в виде:

J = m r 2 ,

где

r = i z

– радиус инерции – расстояние от оси вращения, на котором необходимо разместить массу тела, чтобы момент инерции размещенной массы равнялся моменту инерции тела

относительно этой оси, м.

Для сложных тел, для которых момент инерции математически выразить затруднительно, определяется и задается именно радиус инерции.

Момент инерции тела относительно оси проходящей через его центр масс (центральной оси) всегда наименьший.

Теорема Гюйгенса-Штейнера (рисунок 5.5)

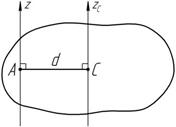Момент инерции тела относительно любой оси равен моменту инерции тела относительно параллельной оси, проходящей через центр его масс плюс произведение массы тела на квадрат

расстояния между этими осями:

Рисунок 5.5 J z = J zс + md 2 .

Моменты инерции некоторых однородных тел

1. Тонкий стержень (рисунок 5.6)

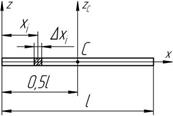Предположим, что стержень длиной l имеет постоянное весьма малое сечение F и плотность

r . Его масса определится:

m = r V = r Fl ,

Рисунок 5.6

где V – объем тела,

м3 .

Разобьем стержень на элементарные участки длиной

Dx i , массы

которых

m i = r FDx i . Тогда момент инерции относительно оси z ,

проходящей перпендикулярно стержню через его край, будет равен:

J = åm x2 = år F x2Dx = r F åx2Dx .

z i i i i i i

Перейдя к пределу суммы, получаем определенный интеграл:

l r Fl3 l2 ml2

J z = r F ò x2dx = = r Fl = .

0 3 3 3

С помощью теоремы Гюйгенса-Штейнера определим момент инерции

стержня J

C

относительно центральной оси z C

параллельной оси z :

J = J - md 2

C

= ml2

3

- ml2

4

ml2

.

12

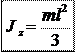Момент инерции тонкого стержня относительно оси z :

.

Момент инерции тонкого стержня относительно оси дящей через центр масс:

z C , прохо-

.

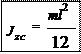2. Круглый диск малой толщины и цилиндр (рисунок 5.7)

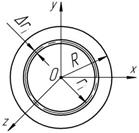Предположим, что круглый диск радиусом R

имеет весьма малую толщину h и плотность r .

m = r V = r hF = r h p R2 .

Разобьем диск на элементарные кольца шириной

Рисунок 5.7

Dr i , массы которых m i = r hF i .

æ Dr ö2 æ Dr ö2

F i = p ç r i + i ÷ - p ç r i - i ÷

= 2p r iDr i ;

è 2 ø è 2 ø

m i = 2r h p r i Dr i .

J = åm r2 = å2r h p r3Dr = 2r h p år3Dr .

Перейдя к пределу суммы, получаем определенный интеграл:

R 4

J z = 2r h p òr3d r = 2r h p

= r h p R

2

= r h p R2=

mR2

.

0 4 2 2 2

Момент инерции круглого диска относительно оси z :

mR2

J z =

. (5.3)

2

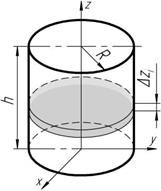Для круглого цилиндра (рисунок 5.8) момент

инерции инерций

J z

DJ z

определим как сумму моментов элементарных пластинок толщиной

Dz i , масса которых m i , относительно той же оси,

Рисунок 5.8

пользуясь формулой (5.3):

å å m R2

R2 å

mR2

2 2 2

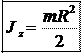Момент инерции круглого цилиндра относительно оси z :

.

+ md 2 .

КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. Что такое механическая система?
2. Как разделяются силы, действующие на механическую систему?
3. Каковы свойства внутренних сил?
4. Как определить центр масс механической системы?
5. Как определяется момент инерции относительно оси?
6. Сформулируйте теорему Теорема Гюйгенса-Штейнера.
7. Запишите формулы для моментов инерции стержня, диска и цилиндра.