Лекция 1. Матрицы.
Раздел 1. Введение
Математическое образование студента начинается с трех основных дисциплин, а именно высшей алгебры, аналитической геометрии и математического анализа. Эти три дисциплины вместе составляют фундамент, на котором строится все здание современной математики.
Высшая алгебра представляет собой естественное обобщение и далеко идущее развитие школьного курса алгебры, где центральным является вопрос о решении уравнений. Изучение уравнений начинается с простого случая одного уравнения первой степени с одним неизвестным, а затем развивается в двух направлениях:
· с одной стороны, рассматриваются системы двух и трех уравнений первой степени с двумя и, соответственно, тремя неизвестными;
· с другой стороны, изучается одно квадратное уравнение с одним неизвестным, а также некоторые частные типы уравнений более высокой степени.
Оба направления получают дальнейшее развитие в курсе высшей алгебры, определяя ее разбиение на два больших раздела: линейную алгебру и алгебру многочленов.
Линейная алгебра имеет исходной задачей изучение произвольных систем уравнений первой степени (линейных уравнений). Для решения таких систем в том случае, когда число уравнений равно числу неизвестных, разработан аппарат теории определителей. Если же число уравнений не равно числу неизвестных, этого аппарата уже недостаточно, и была разработана теория матриц, т.е. систем чисел, разложенных в квадратные или прямоугольные таблицы.
Решением простейших уравнений занимались еще вавилонские, китайские а затем древнегреческие и индийские математики. Вершиной алгебраических исследований этого периода являются сочинения греческого математика Диофанта ( III в. до н.э.).
Большой вклад в развитие алгебры внесли математики средневекового востока, писавшие на арабском языке, особенно узбекский ученый Мухаммед Аль-Хорезми (IХ в.) и таджикский математик и поэт Омар Хайям (1040-1123г.г.).
2. Векторная алгебра и анализ
2.1. Определители, матрицы, системы линейных уравнений
Автор Л.Ю. Трояновская.
Лекция 1. Матрицы.
Содержание:
- Определение матрицы. Виды матриц. ♦
- Операции над матрицами и их свойства. ♦
Определение матрицы. Виды матриц.
Определение 1. Матрицей размерности 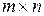 называется прямоугольная таблица чисел
называется прямоугольная таблица чисел 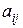 , состоящая из m строк и n столбцов.
, состоящая из m строк и n столбцов.
Обозначение:
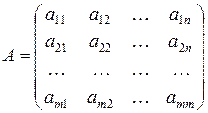 =
= 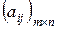 ,
,
где 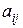 - элемент матрицы, расположенный на пересечении i -той строки и j-того столбца. Элементы
- элемент матрицы, расположенный на пересечении i -той строки и j-того столбца. Элементы 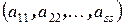 , где
, где 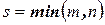 , образуют главную диагональ.
, образуют главную диагональ.
Выражение 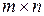 - называется размером (размерностью) матрицы.
- называется размером (размерностью) матрицы.
Строки матрицы будем обозначать 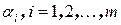 , а столбцы –
, а столбцы – 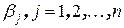 .
.
Определение 2. Матрицы 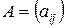 и
и 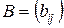 одинаковой размерности равны, если равны их соответствующие элементы:
одинаковой размерности равны, если равны их соответствующие элементы: 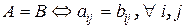 .
.
Замечание. Значок 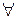 Называется «квантор всеобщности» и означает «для всех», «любой» и т.д.
Называется «квантор всеобщности» и означает «для всех», «любой» и т.д.
Виды матриц.
Определение 3. Если все элементы матрицы равны 0, то матрица называется нулевой, обозначается О:
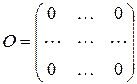 .
.
Нулевая матрица играет роль нуля в операциях над матрицами.
Определение 4. Матрица размера 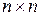 называется квадратной матрицей п – го порядка.
называется квадратной матрицей п – го порядка.
Элементы 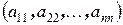 образуют главную диагональ, а элементы
образуют главную диагональ, а элементы 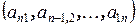 – побочную.
– побочную.
Пример. В матрице
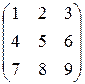
элементы 1, 5, 9 – главная диагональ, а 7, 5, 3 – побочная.
Определение 5. Квадратная матрица называется диагональной, если все ее элементы вне главной диагонали равны нулю: 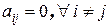 ,
,
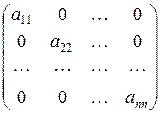 .
.
Определение 6. Диагональная матрица произвольного порядка называется единичной, если все элементы главной диагонали – единицы: 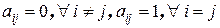 .
.
Обозначение
Е= 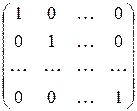 .
.
Единичная матрица играет роль единицы в операциях над матрицами.
Определение 7. Матрица называется матрицей треугольного вида, если все элементы под главной диагональю равны нулю.
Для квадратной матрицы: Для прямоугольной матрицы:
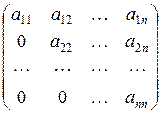
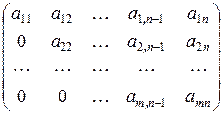
Операции над матрицами и их свойства.
Линейные операции.
Линейными являются операции сложения и умножения на число.
Определение 8. Суммой матриц 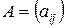 и
и 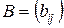 одинаковой размерности называется матрица
одинаковой размерности называется матрица 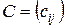 той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых матриц:
той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых матриц: 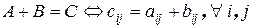 .
.
Пример.
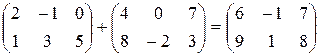 .
.
Определение 9. Произведением матрицы 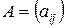 размерности
размерности  на число λ называется матрица
на число λ называется матрица 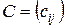 той же размерности, получающаяся из матрицы А умножением всех ее элементов на λ:
той же размерности, получающаяся из матрицы А умножением всех ее элементов на λ: 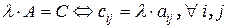 .
.
Пример.
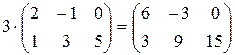 .
.
Определение 10. Матрица 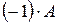 называется противоположной к матрице А и обозначается -А.
называется противоположной к матрице А и обозначается -А.
Основные свойства линейных операций.
1°. А+В=В+А,
2°. (А+В)+С=А+(В+С),
3°. λ∙( А+В)= λ∙ А+λ∙В,
4°. О+А =А,
5°. 0∙А=О,
6°. -А+А =О.
Умножение матриц.
Определение 11. Произведением матрицы 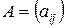 размерности
размерности 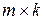 на матрицу
на матрицу 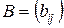 размерности
размерности 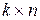 называется матрица
называется матрица 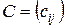 размерности
размерности 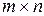 , каждый элемент которой
, каждый элемент которой 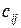 равен сумме произведений соответствующих элементов i -той строки матрицы А и j-того столбца матрицы В:
равен сумме произведений соответствующих элементов i -той строки матрицы А и j-того столбца матрицы В: 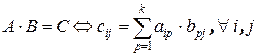 .
.
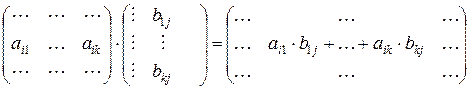 .
.
Пример.
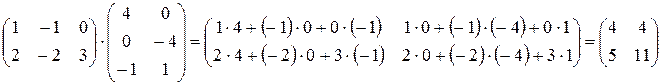
Основные свойства умножения матриц.
1°. (А∙В)∙С=А∙(В∙С),
2°. А∙(В+С)=А∙В+А∙С,
3°. λ∙( А∙В)= (λ∙ А)∙В=А∙(λ∙В),
4°. А∙Е=Е∙А=А.
Замечание. В общем случае, 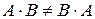 .
.
Если 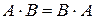 , то матрицы А и В называются перестановочными.
, то матрицы А и В называются перестановочными.
Транспонирование матриц.
Определение 12. Матрица 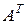 называется транспонированной к матрице А, если для всех ее элементов выполняется условие
называется транспонированной к матрице А, если для всех ее элементов выполняется условие 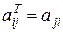 .
.
Пример.
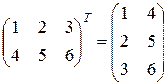 .
.
Основные свойства транспонирования.
1°. 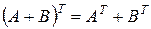 ,
,
2°. 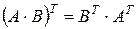 ,
,
3°. 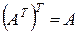 .
.








