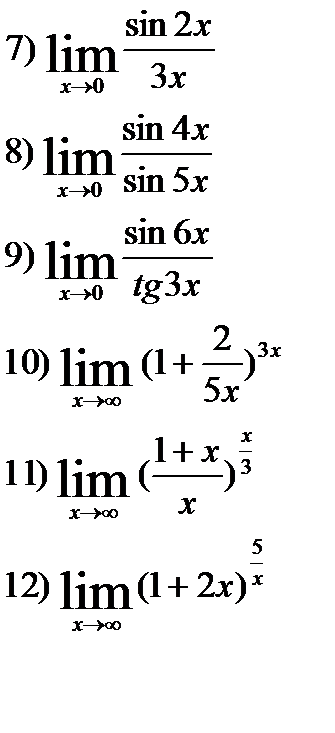Лекция по теме "Предел функции. Замечательные пределы".
1. Ознакомление с теорией предела функции.
Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Записывается предел следующим образом 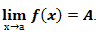 .
.
Вычислим предел: 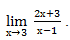
Подставляем вместо х – 3. 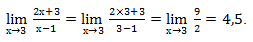
Заметим, что предел числа равен самому числу.
Примеры: вычислите пределы 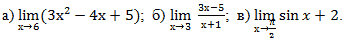
Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция называется непрерывной (в данной точке).
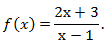
Вычислим значение функции в точке x0 = 3 и значение его предела в этой точке.
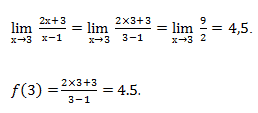
Значение предела и значение функции в этой точке совпадает, следовательно, функция непрерывна в точке x0 = 3.
Но при вычислении пределов зачастую появляются выражения, значение которых не определено. Такие выражения называют неопределённостями.
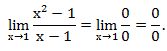
Основные виды неопределенностей: 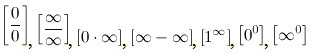
Раскрытие неопределенностей
Для раскрытия неопределенностей используют следующее:
· упрощают выражение функции: раскладывают на множители, преобразовывают функцию с помощью формул сокращенного умножения, тригонометрических формул, домножают на сопряженное, что позволяет в дальнейшем сократить и т.д., и т.п.;
· если предел при раскрытии неопределенностей существует, то говорят, что функция сходится к указанному значению, если такого предела не существует, то говорят, что функция расходится.
Пример: вычислим предел. 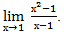
Разложим числитель на множители 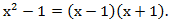
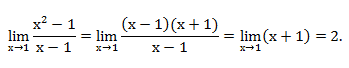
3. Вычисление пределов функции
Пример 1. Вычислите предел функции: 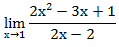
При прямой подстановке, получается неопределенность:
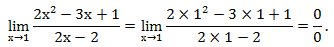
Разложим на множители числитель и знаменатель и вычислим предел.
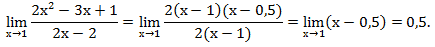
Пример 2. Вычислите предел функции: 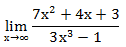
При прямой подстановке, получается неопределенность.
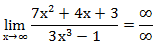
Помножим и числитель, и знаменатель на 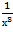 .
.
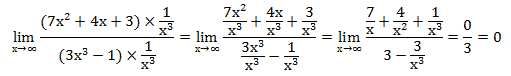
Учтем, что если число разделить на бесконечно большое число получится ноль. То есть предел 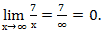 Аналогично
Аналогично 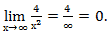
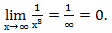
Пример 3. Вычислите предел функции: 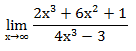
При прямой подстановке, получается неопределенность.
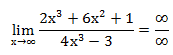
Помножим и числитель, и знаменатель на 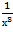 .
.
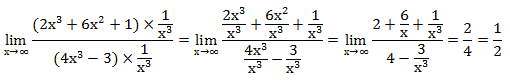
Мы учли, что 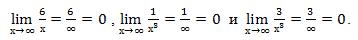
Свойства функции:
Если f(x)=b a g(x)=c то выполняются следующие свойства:
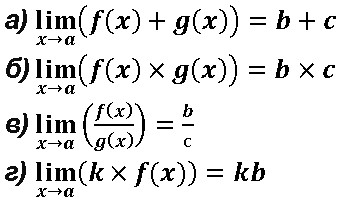
Замечательные пределы.
Первый замечательный предел.
Теорема. Предел отношения sin бесконечно малой величины к самой этой величины к самой этой величине равен 1, т.е. 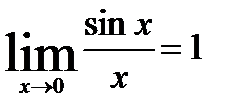 . Или
. Или 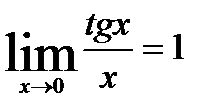
Теорема. Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен единице, то есть 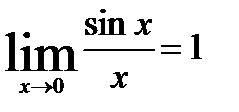 Этот предел называют первым замечательным пределом. С его помощью вычисляют пределы выражений, содержащих тригонометрические функции.
Пример 1. Вычислить
Этот предел называют первым замечательным пределом. С его помощью вычисляют пределы выражений, содержащих тригонометрические функции.
Пример 1. Вычислить 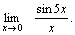 Решение. Преобразуем данное выражение:
Решение. Преобразуем данное выражение: 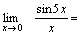 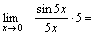 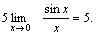 Пример 2. Найти
Пример 2. Найти 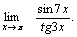 Решение. Для того чтобы воспользоваться первым замечательным пределом, перейдем к новой переменной
Решение. Для того чтобы воспользоваться первым замечательным пределом, перейдем к новой переменной 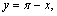 которая при которая при 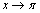 стремится к нулю. Тогда имеем стремится к нулю. Тогда имеем 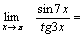 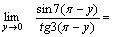 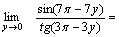 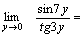 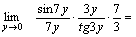 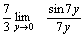 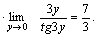 Второй замечательный предел:
Второй замечательный предел: 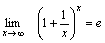 или или 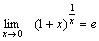 или или 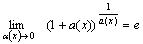 , , 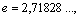 Пример 3. Найти
Пример 3. Найти 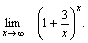 Решение. Полагая
Решение. Полагая 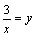 , получим: , получим: 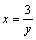 и и 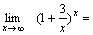 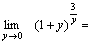 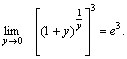 Пример 4. Найти
Пример 4. Найти 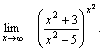 Решение. Преобразуем выражение, стоящее под знаком предельного перехода.
Решение. Преобразуем выражение, стоящее под знаком предельного перехода.
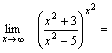 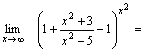 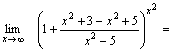 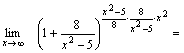 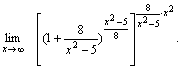 Так как
Так как 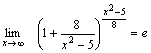 , а , а 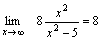 , то , то 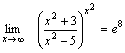 .
Для зачета по теме «Пределы», необходимо решить зачетную работу .
Для зачета по теме «Пределы», необходимо решить зачетную работу
|
Зачетная работа по теме «Пределы».
Вычислите пределы:
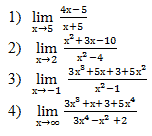 5)
5) 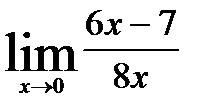 6) Найти предел функции:
6) Найти предел функции: 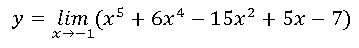
|