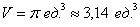Урок « Вычисление объема тела вращения с помощью определенного интеграла»
Цели урока: научиться вычислять объем тел вращения с помощью определенного интеграла.
Повторить:
1. Формулу Ньютона-Лейбница для нахождения значения определенного интеграла
2. Таблицу первообразных.
Представьте некоторую плоскую фигуру на координатной плоскости. Данную фигуру можно ещё и вращать, причем вращать двумя способами:
– вокруг оси абсцисс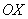 
;
– вокруг оси ординат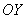 
.
Пример 1
Вычислить объем тела, полученного вращением фигуры, ограниченной линиями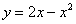 
, 
вокруг оси .
Решение:
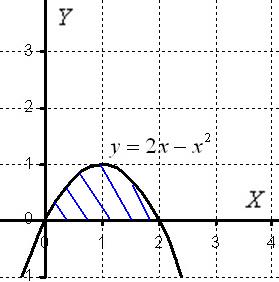
Искомая плоская фигура заштрихована синим цветом, именно она и вращается вокруг оси .
Объем тела вращения можно вычислить по формуле:
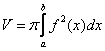
Вычислим объем тела вращения, используя данную формулу:
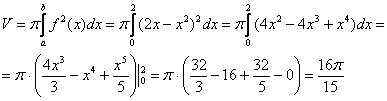
Ответ: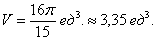 
Пример 2
Найти объем тела, образованного вращением вокруг оси 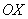фигуры, ограниченной линиями 
, , 
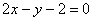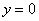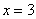
Решение: Выполним чертеж:
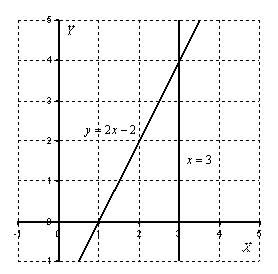
Объем тела вращения:
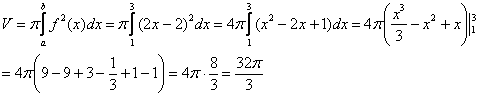
Ответ: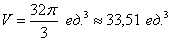 
Пример 3
Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиям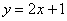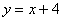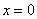и 
, 
, 
и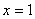 
Решение: Изобразим на чертеже плоскую фигуру, ограниченную линиями 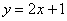, , 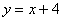, , 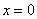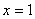не забывая при этом, что уравнение 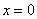задает ось :
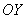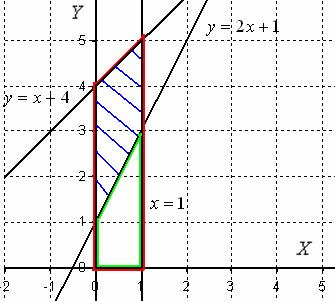
Искомая фигура заштрихована синим цветом. При её вращении вокруг оси получается такой сюрреалистический бублик с четырьмя углами.
Объем тела вращения вычислим как разность объемов тел.
Сначала рассмотрим фигуру, которая обведена красным цветом. При её вращении вокруг оси получается усеченный конус. Обозначим объем этого усеченного конуса через 
.
Рассмотрим фигуру, которая обведена зеленым цветом. Если вращать данную фигуру вокруг оси 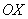, то получится тоже усеченный конус, только чуть поменьше. Обозначим его объем через 
.
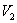И, очевидно, разность объемов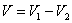 
– в точности объем нашего «бублика».
Используем стандартную формулу для нахождения объема тела вращения:
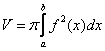
1) Фигура, обведенная красным цветом ограничена сверху прямой 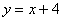, поэтому:
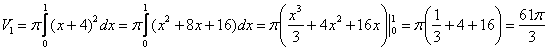
2) Фигура, обведенная зеленым цветом ограничена сверху прямой 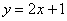, поэтому:
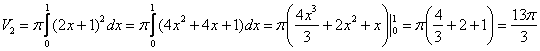
3) Объем искомого тела вращения: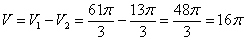 
Ответ: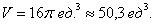 
Пример 4
Вычислить объем тела, образованного вращением относительно оси 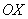плоской фигуры, ограниченной линиями 
, 
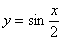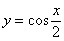, где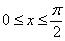 
.
Пример 4: Решение: Выполним чертеж:
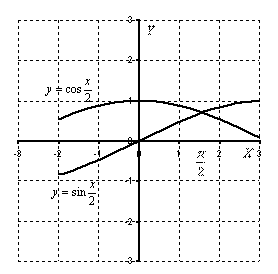
Объем тела вращения вычислим как разность объемов при помощи формулы:
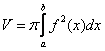
В данном случае:
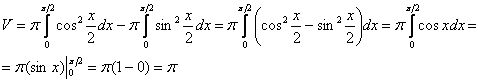
Ответ: 