Эмпирические константы равновесия и их взаимосвязь
Лекция 6
ХИМИЧЕСКОЕ РАВНОВЕСИЕ
Закон действующих масс
Итак, в предыдущей лекции было показано, что критерием направления протекания реакций и состояния равновесия при постоянстве температуры и давления (p , T - const), является изменение энергии Гиббса.
ΔG<0 – самопроизвольно протекает реакция в прямом направлении;
ΔG>0 – самопроизвольно протекает реакция в обратном направлении;
ΔG=0 – устанавливается равновесие (химическое, фазовое).
Все химические реакции в той или иной степени обратимы: наряду с химическим взаимодействием исходных веществ (прямая реакция) протекает взаимодействие между продуктами (обратная реакция), в результате которой снова образуются исходные вещества. По мере протекания процесса скорость прямой реакции уменьшается (количество молекул исходных веществ понижается), а скорость обратной реакции (по мере накопления молекул продуктов) возрастает. Когда обе скорости сравняются, наступает состояние химического равновесия – число молекул, составляющих систему, перестает меняться и остается постоянным во времени при неизменных внешних условиях. Химическое равновесие является подвижным – с изменением внешних параметров может смещаться в ту или иную сторону.
Равновесия могут быть классифицированы по различным признакам. Например, различают устойчивые, неустойчивые, безразличные и т.д. Для устойчивого равновесия характерно то, что к нему принципиально можно прийти с двух разных сторон.
Устойчивое равновесие является динамическим. Равновесное состояние сохраняется во времени постоянным не вследствие отсутствия процессов, а вследствие протекания их одновременно в двух противоположных направлениях с одинаковой скоростью. Термодинамически устойчивое равновесие иногда называют «истинным равновесием». Условием термодинамического равновесия является минимум энергии Гиббса (ΔG=0).
Например, в обратимой гомогенной реакции
Н2(г)+I2(г)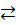 
2HI(г)
Соотношение скоростей прямой и обратной реакций согласно закону действующих масс зависит от соотношения концентраций реагирующих веществ, а именно: скорость прямой реакции
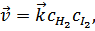
Скорость обратной реакции: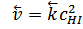 
,
где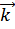 
, 
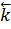- константы скорости прямой и обратной реакций.
Если Н2 и I2 – исходные вещества, то в первый момент скорость прямой реакции определяется их начальными концентрациями, а скорость обратной
реакции равна нулю. По мере расходования исходных веществ и образования продуктов скорость прямой реакции уменьшается, а скорость обратной возрастает. Спустя некоторое время обе скорости уравниваются и в системе устанавливается химическое равновесие.
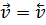, тогда 
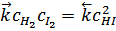или 
.
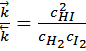Поскольку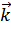 
и 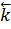при данной температуре постоянны, то и их отношение будет постоянным. Обозначим его через К, получим
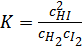
K называют константой химического равновесия, а приведенное уравнение является одним из выражений закона действующих масс, установленным эмпирическим путем норвежскими учёными Гульдбергом и Вааге в 1867 году.
Произведение равновесных концентраций продуктов реакции деленое на произведение равновесных концентраций исходных веществ, с учётом всех стехиометрических коэффициентов, есть величина постоянная.
Это «кинетический» вариант вывода уравнения закона действующих масс для химического равновесия. Он справедлив только для сравнительно простых реакций. В общем случае следует использовать термодинамический вывод.
Эмпирические константы равновесия и их взаимосвязь
Для обратимой реакции, где все реагенты идеальные газы
,
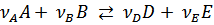согласно закону действующих масс, выразим константу равновесия через равновесные концентрации реагентов. Концентрационная константа – эмпирическая константа равновесия равна
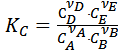, где с i – равновесная молярная концентрация.
Размерность константы: [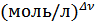 
] и др.
Для идеальных газов константу можно выразить через равновесные парциальные давления
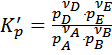, где pi – равновесное парциальное давление.
Размерность константы: [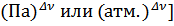 
Используя уравнение Менделеева-Клапейрона, выведем уравнение, связывающее эти выражения:
; 
; 
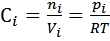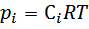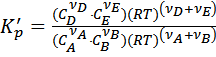
Или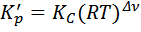 
Константу равновесия можно выразить через равновесную мольную долю (xi) или через равновесное число моль реагентов (ni):
; 
;
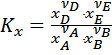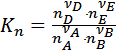С учётом того, что: pi=xi × p (закон Дальтона для ид. газов)
И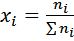 
Получим следующие уравнения:
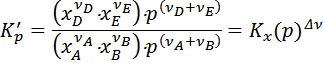
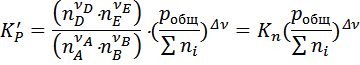
Где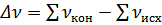 
.
Для реальных газов константа равновесия может быть выражена через равновесные фугитивности (летучести)
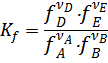
Где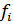 
- равновесная фугитивность (летучесть) i -того газа.
Летучесть связана с давлением уравнением:
f = g × р
g - коэффициент летучести (фугитивности).
Коэффициент летучести это мера отклонения поведения реального газа от идеального. При низких давлениях коэффициент летучести равен 1, и газ можно считать идеальным.
Если реакция протекает в конденсированных средах, например, в растворах, то константа равновесия должна быть выражена через активности.
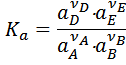
Где ai – активность i -того компонента. Активность равна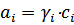 
, где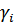 
- коэффициент активности. Активность безразмерная величина и константа, выраженная через активности, является термодинамической константой. Для идеальных растворов 
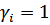, тогда будет справедлива концентрационная константа.
Термодинамическая константа равновесия
Равновесные системы это многокомпонентные системы. Для обратимых равновесных процессов можно записать:
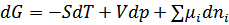
Где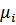 
- химический потенциал i -того компонента, 
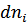- изменение количества моль i -того компонента.
Химический потенциал есть частная производная энергии Гиббса по числу моль компонента при постоянстве давления, температуры, чисел моль всех компонентов, кроме данного:
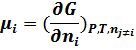
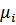- парциальная мольная величина энергии Гиббса.
Химический потенциал численно равен изменению энергии Гиббса при добавлении в бесконечно большую систему (настолько большую, что прибавление 1 моль вещества не изменяет её состав) одного моля i -того компонента.
Для чистого вещества химический потенциал равен его молярной энергии Гиббса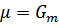 
.
Для идеальных газов: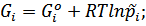 
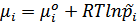
Где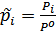 
- отнесенное давление (отнесенное к 1 атмосфере, поэтому безразмерная величина).
Принцип повсеместного равенства химического потенциала
Все химические и физико-химические процессы протекают в сторону уменьшения химического потенциала до тех пор, пока химический потенциал каждого компонента в каждой точке системы не станет одинаковым. В состоянии химического равновесия
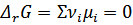
Для обратимой реакции, где все реагенты идеальные газы
,
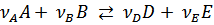используя уравнение для идеального газа,
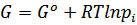
где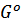 
- стандартная энергия Гиббса (т.е. энергия Гиббса при давлении 1 атм.), получим:
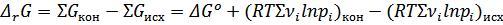
Где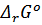 
- стандартная энергия Гиббса реакции. Преобразовав уравнение получим:
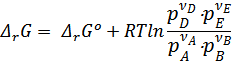
Это уравнение получило название изотермы Вант-Гоффа.
При равновесии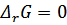 
, тогда
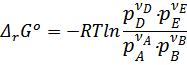
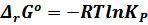
Здесь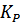 
- термодинамическая константа равновесия. Она не зависит от давления, а зависит только природы реагирующих веществ и температуры.
Или в общем виде уравнение изотермы Вант-Гоффа записывается как:
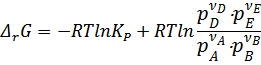
Связь между эмпирической и термодинамической константой
Чтобы установить взаимосвязь между эмпирически найденной величиной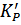 
и термодинамическими константами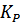 
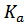(Ко) следует выразить парциальные давления каждого компонента в долях от стандартного (1 атм.). С учётом этого приходим к выражению:
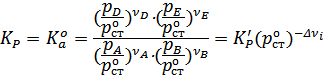
И аналогично можно вывести уравнения, связывающие термодинамическую константу и константы, выраженных через равновесные концентрации, мольные доли и количество моль реагентов.
Равновесия в гетерогенных процессах
Реакции называются гетерогенными, если реагирующие вещества находятся в разных фазах. В простейшем случае имеющиеся конденсированные фазы практически нерастворимы друг в друге. Тогда активности конденсированных фаз принимаются равными единице, а активности компонентов газовой фазы – их парциальным давлениям (или летучести, когда давления сопоставимы с критическими).
Примером простой гетерогенной реакции является термическая диссоциация карбоната кальция:
CaCO3(тв)=СaO(тв)+СО2(г)
; 
. 
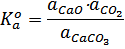
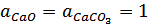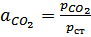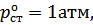тогда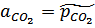 
.
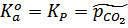
То есть термодинамическая константа численно равна равновесному давлению СО2 , выраженному в атмосферах.
Стандартные условия, когда давление равно стандартному, т.е.
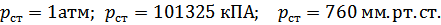
А газы, участвующие в реакции, являются идеальными.