Лінійна залежність векторів
Означення. Система векторів 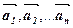 називається лінійно залежною, якщо існують такі числа
називається лінійно залежною, якщо існують такі числа 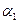 ,
, 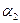 ,…
,… 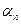 , серед яких хоча б одне відмінне від нуля, що
, серед яких хоча б одне відмінне від нуля, що 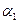
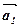 +
+ 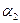
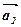 + … +
+ … + 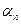
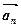 = 0. / 4/
= 0. / 4/
Якщо ж рівність /4/ справджується тільки при 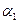 =
= 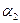 =…=
=…= 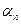 = 0, то дана система векторів називається лінійно незалежною.
= 0, то дана система векторів називається лінійно незалежною.
Сума 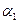
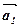 +
+ 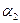
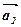 + … +
+ … + 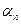
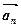 називається лінійною комбінацією векторів
називається лінійною комбінацією векторів 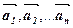 .
.
Розглянемо деякі властивості лінійної залежності векторів, які будуть потрібні надалі.
Властивість 1. Система векторів лінійно залежна тоді і тільки тоді, коли хоча б один з векторів є лінійною комбінацією інших векторів цієї системи.
Доведення.
1. Необхідність. Нехай система векторів 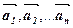 лінійно залежна. Тоді існують такі числа
лінійно залежна. Тоді існують такі числа 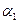 ,
, 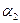 ,…,
,…, 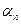 , що
, що 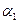
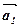 +
+ 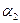
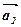 + … +
+ … + 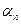
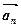 = 0 /5/
= 0 /5/
При цьому принаймні одне з чисел 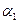 ,
, 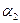 ,…,
,…, 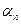 не дорівнює нулю. Нехай, наприклад,
не дорівнює нулю. Нехай, наприклад, 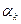
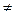 0. Тоді з рівності /5/ дістанемо:
0. Тоді з рівності /5/ дістанемо:
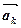 = –
= – 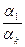
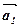 –
– 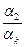
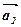 –
– 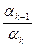
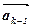 –
– 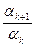
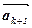 –
– 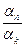
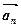 .
.
Отже, вектор 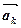 є лінійною комбінацією векторів
є лінійною комбінацією векторів 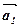 ,
, 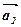 ,…
,… 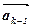 ,
, 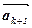 ,…,
,…, 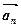 .
.
3. Достатність. Нехай у даній системі векторів вектор 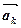 є лінійною комбінацією інших векторів:
є лінійною комбінацією інших векторів:
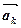 =
= 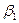
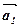 +
+ 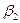
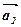 + … +
+ … + 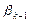
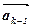 +
+ 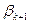
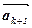 + … +
+ … + 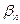
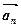 .
.
Цю рівність можна записати так:
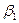
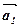 +
+ 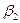
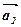 + … +
+ … + 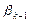
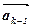 + (-1)
+ (-1) 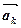 +
+ 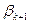
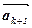 + … +
+ … + 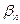
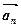 = 0.
= 0.
У цій рівності коефіцієнт біля 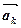 відмінний від нуля, тому дана система векторів лінійно залежна.
відмінний від нуля, тому дана система векторів лінійно залежна.
Властивість 2. Якщо частина даної системи векторів лінійно залежна, то і вся система векторів лінійно залежна.
Властивість 3. Якщо система векторів лінійно незалежна, то будь-яка її частина також лінійно незалежна.
Ця властивість безпосередньо випливає із властивості 2, бо якби деяка частина даної системи векторів була лінійно залежною, то і вся система була б лінійно залежною.
Властивість 4. Система лінійно незалежних векторів не містить нульового вектора.
Якщо в деякій системі векторів є нульовий вектор: 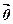 ,
, 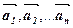 , то
, то
виконується рівність 1* 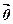 + 0*
+ 0*  +… + 0*
+… + 0* 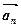 =0. 1
=0. 1 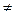 0, тому така система є лінійно залежною, а, отже, система лінійно незалежних векторів не може містити нульового вектора.
0, тому така система є лінійно залежною, а, отже, система лінійно незалежних векторів не може містити нульового вектора.
Для системи двох і трьох векторів поняття лінійної залежності тісно пов'язане з колінеарністю і компланарністю векторів. Справедливі такі теореми.
Теорема 1. Два вектори  і
і  лінійно залежні тоді і тільки тоді, коли вони колінеарні.
лінійно залежні тоді і тільки тоді, коли вони колінеарні.
Доведення.
1. Необхідність. Нехай система векторів  ,
,  лінійно залежна. Тоді за
лінійно залежна. Тоді за
властивістю 1 один із векторів лінійно виражається через другий:  = α
= α  ,
,
звідки випливає, що вектори  і
і  колінеарні.
колінеарні.
2. Достатність. Нехай вектори  і
і  колінеарні. Тоді існує таке число α, що
колінеарні. Тоді існує таке число α, що  = α
= α  . Із властивості 1 випливає, що вектори
. Із властивості 1 випливає, що вектори  і
і  лінійно залежні. Теорему доведено.
лінійно залежні. Теорему доведено.
Теорема 2. Система трьох векторів  ,
,  ,
, 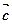 лінійно залежна тоді і тільки тоді, коли ці вектори компланарні.
лінійно залежна тоді і тільки тоді, коли ці вектори компланарні.
Доведення.
1. Необхідність. Нехай система векторів  ,
,  ,
, 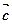 лінійно залежна. Тоді за властивістю 1 один із векторів є лінійною комбінацією інших векторів. Нехай, наприклад,
лінійно залежна. Тоді за властивістю 1 один із векторів є лінійною комбінацією інших векторів. Нехай, наприклад,  = α
= α  +β
+β 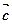 . Із означення суми векторів випливає, що вектори
. Із означення суми векторів випливає, що вектори  , α
, α  , β
, β 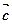 компланарні, а тоді і вектори
компланарні, а тоді і вектори  ,
,  ,
, 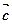 будуть компланарними, бо
будуть компланарними, бо  || α
|| α  ,
, 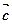 || β
|| β 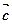 .
.
2. Достатність. Нехай вектори  ,
,  ,
, 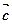 компланарні. Якщо
компланарні. Якщо  ||
||  , то за попередньою теоремою вектори
, то за попередньою теоремою вектори  ,
,  лінійно залежні, а за властивістю 2 лінійно залежними будуть і вектори
лінійно залежні, а за властивістю 2 лінійно залежними будуть і вектори  ,
,  ,
, 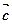 . Якщо ж
. Якщо ж  не ||
не ||  , то за теоремою про розклад вектора за двома не колінеарними векторами
, то за теоремою про розклад вектора за двома не колінеарними векторами  = α
= α  +β
+β 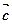 . То за властивістю 1 система векторів
. То за властивістю 1 система векторів  ,
,  ,
, 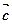 лінійно залежна. Теорему доведено
лінійно залежна. Теорему доведено
4. Координати вектора
Нехай (  ,
,  ,
,  ) деякий базис простору
) деякий базис простору 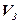 ,
,  – довільний вектор цього простору. За теоремою про розклад вектора за трьома некомпланарними векторами існують єдині числа
– довільний вектор цього простору. За теоремою про розклад вектора за трьома некомпланарними векторами існують єдині числа 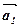 ,
, 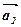 ,
, 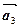 такі, що
такі, що
 =
= 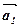
 +
+ 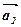
 +
+ 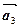
 .
.
Коефіцієнти  ,
,  ,
,  розкладу вектора за базисними векторами називаються координатами вектора в даному базисі. При цьому число
розкладу вектора за базисними векторами називаються координатами вектора в даному базисі. При цьому число  називається першою координатою, число
називається першою координатою, число  – другою, а число
– другою, а число  – третьою.
– третьою.
Якщо вектор  в даному базисі має координати
в даному базисі має координати  ,
,  ,
,  , то скорочено це записують так:
, то скорочено це записують так:  (
(  ,
,  ,
,  ) або
) або 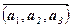 .
.
Встановимо геометричний зміст координат вектора в даному базисі. Для цього відкладемо вектори  ,
,  ,
,  і
і  від деякої точки О простору (мал. 16):
від деякої точки О простору (мал. 16):  =
= 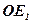 ,
,  =
= 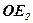 ,
,  =
= 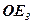 ,
,  =
= 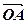 .
.
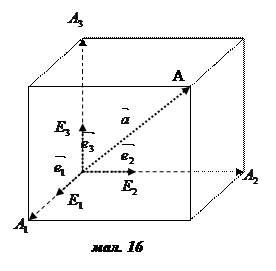
Побудуємо паралелепіпед, ребра якого напрямлені вздовж прямих 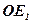 ,
, 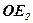 ,
, 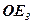 , а діагоналлю є відрізок OA. Тоді
, а діагоналлю є відрізок OA. Тоді  =
= 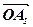 +
+ 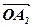 +
+ 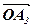 , де
, де 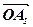 =
= 
 ,
, 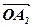 = =
= = 
 ,
, 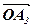 =
= 
 .
.
Тому 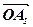 =
= 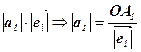 ;
;
 > 0, якщо
> 0, якщо 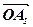
 і
і  < 0, якщо
< 0, якщо 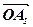
 ;
;
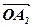 =
= 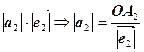 ;
;
 > 0, якщо
> 0, якщо 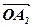
 і
і  < 0, якщо
< 0, якщо 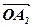
 .
.
Аналогічно, 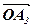 =
= 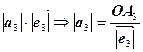 ;
;
 > 0, якщо
> 0, якщо 
 і
і  < 0,
< 0, 
 .
.
Отже, координата  з точністю до знака дорівнює довжині відрізка
з точністю до знака дорівнює довжині відрізка 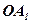 виміряному в одиницях довжини
виміряному в одиницях довжини  . Знак же координати
. Знак же координати  залежить від напрямку векторів
залежить від напрямку векторів 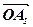 і
і  :
:  > 0, якщо
> 0, якщо 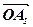
 і
і  < 0, якщо
< 0, якщо 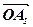
 . Аналогічно зміст двох інших координат
. Аналогічно зміст двох інших координат  і
і  .
.
Базисні вектори в самому базисі мають координати  (1; 0; 0),
(1; 0; 0),  (0; 1; 0),
(0; 1; 0),  (0; 0; 1).
(0; 0; 1).
Аналогічно визначаються координати вектора в просторі 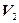 . Базис цього підпростору складається з двох не колінеарних векторів. Нехай система векторів
. Базис цього підпростору складається з двох не колінеарних векторів. Нехай система векторів  ,
,  є базисом підпростору
є базисом підпростору 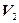 . Тоді за теоремою про розклад вектора за двома не колінеарними векторами для будь-якого вектора
. Тоді за теоремою про розклад вектора за двома не колінеарними векторами для будь-якого вектора  із підпростору
із підпростору 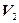 існують єдині числа
існують єдині числа  ,
,  такі, що
такі, що  =
= 
 +
+ 
 . Коефіцієнти
. Коефіцієнти  ,
,  цього розкладу називаються координатами вектора
цього розкладу називаються координатами вектора  в базисі (
в базисі (  ,
,  ). Число
). Число  називається першою координатою, а число
називається першою координатою, а число  – другою.
– другою.
Аналогічним є і геометричний зміст координат вектора в підпросторі  (мал. 17):
(мал. 17):
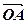 =
= 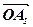 +
+ 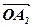 =
= 
 +
+ 
 .
.
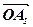 =
= 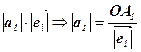 ,
,
 > 0, якщо
> 0, якщо 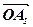
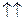
 і
і  < 0, якщо
< 0, якщо 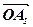
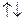
 ;
;
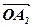 =
= 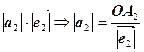 ;
;
 > 0, якщо
> 0, якщо 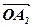
 і
і  < 0, якщо
< 0, якщо 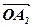
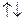
 .
.
Базисні вектори мають координати:  (1; 0),
(1; 0),  (0; 1). Координати вектора в даному базисі повністю задають вектор.
(0; 1). Координати вектора в даному базисі повністю задають вектор.
Розглянемо властивості координат векторів.
Теорема (2-га ознака рівності векторів): для того, щоб два вектори були рівними, необхідно і достатньо, щоб були рівними їх відповідні координати.
Твердження цієї теореми очевидне, воно випливає з єдиності розкладу вектора за трьома не компланарними векторами.
Теорема: справедливі такі твердження:
1) координати суми двох векторів дорівнюють сумі відповідних координат цих векторів;
2) координати різниці двох векторів дорівнюють різниці відповідних координат цих векторів;
3) координати добутку вектора на число дорівнюють добутку відповідних координат цього вектора на дане число.
Доведення: доведемо наприклад перше твердження. Нехай у деякому базисі (  ,
,  ,
,  ),
),  (
(  ,
,  ,
,  ),
),  (
(  ,
,  ,
, 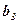 ). Тоді за означенням координат вектора
). Тоді за означенням координат вектора
 =
= 
 +
+ 
 +
+ 
 ,
,  =
= 
 +
+ 
 +
+ 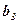
 .
.
Отже,  +
+  =
= 
 +
+ 
 +
+ 
 +
+ 
 +
+ 
 +
+ 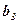
 = (
= (  +
+  )
)  + (
+ (  +
+  )
)  + (
+ (  +
+ 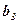 )
)  .
.
Звідси випливає, що координати вектора  +
+  відповідно дорівнюють
відповідно дорівнюють  + +
+ +  ,
,  +
+  ,
,  +
+ 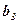 , що й треба було довести.
, що й треба було довести.
Аналогічно доводяться й інші властивості.
Теорема (2-га ознака колінеарності двох векторів): для того, щоб два вектори  (
(  ,
,  ,
,  ),
),  (
(  ,
,  ,
, 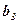 ) задані в деякому базисі (
) задані в деякому базисі (  ,
,  ,
,  ), були колінеарними, необхідно і достатньо, щоб їх координати були пропорційними.
), були колінеарними, необхідно і достатньо, щоб їх координати були пропорційними.
Доведення: якщо  =
= 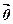 , то твердження очевидне. Припустимо, що
, то твердження очевидне. Припустимо, що 
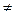
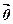 .
.
1. Необхідність. Нехай  ||
||  . Тоді існує таке число λ, що
. Тоді існує таке число λ, що  = λ
= λ  , звідки випиває, що
, звідки випиває, що  = λ
= λ  ,
,  = λ
= λ  ,
,  = λ
= λ 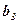 ;
;
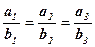 = λ.
= λ.
Отже, якщо вектори колінеарні, то їх координати пропорційні.
2. Достатність. Нехай 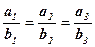 = λ, тоді
= λ, тоді  = λ
= λ  ,
,  = λ
= λ  ,
,  = λ
= λ 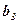 . Помноживши ці рівності на вектори
. Помноживши ці рівності на вектори  ,
,  ,
,  відповідно, дістанемо
відповідно, дістанемо 
 = λ
= λ 
 ,
, 
 = λ
= λ 
 ,
, 
 = λ
= λ 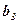
 . Додавши ці рівності дістанемо
. Додавши ці рівності дістанемо 
 +
+ 
 +
+ 
 = λ
= λ 
 + λ
+ λ 
 + λ
+ λ 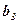
 або
або 
 +
+ 
 +
+ 
 = λ(
= λ( 
 +
+ 
 +
+ 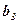
 ), тобто
), тобто  = λ
= λ 
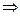
 ||
||  . Теорему доведено.
. Теорему доведено.
5. Тривимірний векторний простір і його підпростори
Побудована нами не порожня множина вільних векторів, у якій введені операції додавання векторів, множення вектора на число, що задовольняють зазначені властивості, а саме:
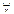
 ,
,  :
:  +
+  =
=  +
+  ;
;
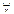
 ,
,  ,
, 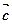 :(
:(  +
+  ) +
) + 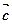 =
=  + (
+ (  +
+ 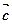 );
);
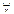
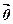 ,
,  :
: 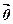 +
+  =
=  +
+ 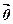 =
=  ;
;
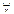

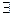 (-
(-  ):
):  + (-
+ (-  ) =
) = 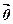 ;
;
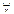
 : 1*
: 1*  =
=  ;
;
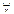 α, β
α, β 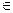 R,
R, 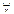
 : α(β
: α(β  ) = (αβ)
) = (αβ)  ;
;
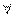 α, β
α, β 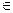 R,
R, 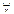
 : (α + β)
: (α + β)  = α
= α  + β
+ β  ;
;
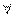
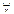 α
α 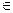 R,
R, 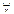
 ,
,  : α(
: α(  +
+  ) = α
) = α  + α
+ α  – називається векторним простором. Позначимо його
– називається векторним простором. Позначимо його 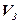 .
.
У векторних просторах розглядається поняття базису векторного простору і розмірності. Введемо означення цих понять.
Означення: базисом векторного простору називається система векторів, яка задана в певному порядку і задовольняє умови:
1) ця система векторів лінійно незалежна;
2) будь-який інший вектор із даного векторного простору є лінійною комбінацією даної системи векторів.
Інакше кажучи, базисом векторного простору називається максимальна система лінійно незалежних векторів даного векторного простору.
Означення: розмірністю векторного простору називається число векторів базису, тобто максимальна кількість лінійно незалежних векторів.
З попередніх теорем випливає, що базисом побудованого нами векторного простору є будь-яка система трьох не компланарних векторів, взятих у певному порядку. Справді, система будь-яких трьох некомланарних векторів лінійно незалежна, а за теоремою про розклад вектора за трьома не компланарними векторами будь-який вектор із даного векторного простору є лінійною комбінацією даної системи векторів.
Тому розмірність даного простору 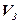 дорівнює трьом. У зв’язку з цим побудований нами векторний простір називається тривимірним векторним простором.
дорівнює трьом. У зв’язку з цим побудований нами векторний простір називається тривимірним векторним простором.
Означення: нехай L – непорожня множина векторів із векторного простору 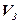 . Множина L називається векторним підпростором простору
. Множина L називається векторним підпростором простору 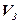 , якщо виконуються такі умови:
, якщо виконуються такі умови:
1) якщо 
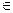 L,
L, 
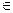 L, то
L, то  +
+ 
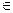 L;
L;
2) якщо 
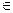 L, то і α
L, то і α 
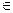 L
L 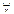 α
α  R.
R.
Тобто підмножина L простору 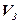 буде векторним підпростором простору
буде векторним підпростором простору 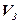 , якщо вона сама є векторним простором.
, якщо вона сама є векторним простором.
6. Скалярний добуток векторів

Нехай  ,
,  − ненульові вектори. Відкладемо від деякої точки O вектори
− ненульові вектори. Відкладемо від деякої точки O вектори 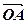 =
=  ,
, 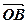 =
=  . Кутом між векторами
. Кутом між векторами  і
і  називається кут між променями OA і OB (мал. 18). Позначають: (
називається кут між променями OA і OB (мал. 18). Позначають: (  ,
,  ) = φ. Для будь-яких векторів
) = φ. Для будь-яких векторів  і
і  маємо 0 ≤ (
маємо 0 ≤ (  ,
,  ) ≤ π.
) ≤ π.
Означення: скалярним добутком двох векторів називається число, яке дорівнює добутку їх довжин на косинус кута між ними: 
 =
= 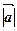
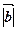 cos(
cos(  ,
,  ).
).
Теорема: скалярний добуток векторів  (
(  ,
,  ,
,  ),
),  (
(  ,
,  ,
, 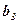 ), заданих в ортонормованому базисі, обчислюються за формулою:
), заданих в ортонормованому базисі, обчислюються за формулою:

 =
= 
 +
+ 
 +
+ 
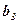 . /6/
. /6/
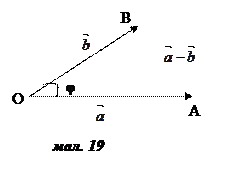
Доведення. Якщо один із векторів або обидва нульові, то формула очевидна. Припустимо, що 
 ,
, 
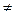
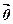 і розглянемо два випадки.
і розглянемо два випадки.
1. Вектори  і
і  не колінеарні. Відкладемо вектори
не колінеарні. Відкладемо вектори 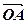 =
=  ,
, 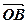 =
=  (мал. 19). Нехай (
(мал. 19). Нехай (  ,
,  ) = φ.
) = φ.
З 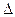 OAB за теоремою косинусів
OAB за теоремою косинусів 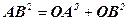 – 2 OAOBcosφ, або
– 2 OAOBcosφ, або 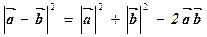 ,
,
звідки 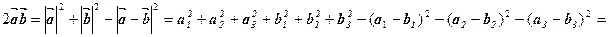
= 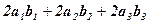 . Отже,
. Отже, 
 =
= 
 +
+ 
 +
+ 
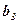 .
.
2. Вектори  і
і  колінеарні. Тоді
колінеарні. Тоді  = λ
= λ  ,
,  = λ
= λ  ,
,  = λ
= λ  ,
,  = λ
= λ 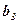 ;
;

 = λ
= λ 
 =
= 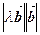 cos(λ
cos(λ  ,
,  ) = λ
) = λ 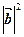 = λ(
= λ( 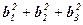 ) = λ
) = λ 
 + λ
+ λ 
 + λ
+ λ 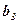
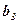 =
= 
 +
+ 
 +
+ 
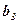
Теорему доведено.
З теореми і означення випливають такі властивості скалярного добутку векторів:
1. 
 = 0 тоді і тільки тоді, коли
= 0 тоді і тільки тоді, коли 
 , якщо
, якщо 
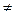
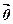 ,
, 
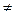
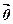 .
.
2. 
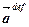 =
= 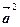 =
= 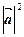
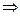
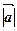 =
= 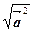 .
.
3. 
 =
= 
 .
.
4. (α  )
)  = α(
= α( 
 ),
), 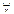 α
α 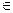 R;
R;
5. (  +
+  )
) 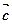 =
= 
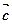 +
+ 
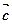 .
.
Формула, аналогічна до формули /6/, має місце і в просторі 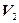 . Справді, нехай в ортонормованому базисі простору
. Справді, нехай в ортонормованому базисі простору 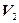 задано вектори
задано вектори  (
(  ,
,  ),
),  (
(  ,
,  ). Тоді, користуючись властивостями 1–5, дістанемо:
). Тоді, користуючись властивостями 1–5, дістанемо: 
 = (
= ( 
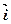 +
+ 
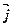 )(
)( 
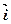 +
+ 
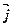 )=
)= 

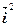 + (
+ ( 
 +
+ 
 )
) 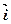
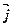 +
+ 

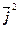 =
= 
 +
+ 
 . Отже,
. Отже, 
 =
= 
 +
+ 
 /7/
/7/
З означення скалярного добутку і /6/, /7/ випливають такі формули для обчислення косинуса кута між векторами:
– у просторі 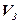 :
:
cos(  ,
,  ) =
) = 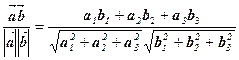 ;
;
– в просторі 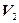 :
:
cos(  ,
,  ) =
) = 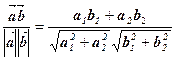 .
.
Векторна алгебра може ефективно використовуватися для розв’язування задач елементарної геометрії.








