Додавання векторів, властивості операції додавання векторів

Введемо операцію додавання векторів, яка відіграє важливу роль в векторній алгебрі.
Означення. Нехай задано два вектори  і
і  . Від деякої точки A відкладемо вектор
. Від деякої точки A відкладемо вектор 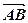 =
=  , потім від точки B відкладемо вектор
, потім від точки B відкладемо вектор 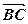 =
=  . Вектор
. Вектор 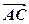 =
= 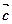 називається сумою векторів
називається сумою векторів  і
і  і позначається так:
і позначається так: 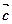 =
=  +
+  (мал. 5). Помітимо, що для знаходження двох неколінеарних векторів доводиться будувати трикутник. Тому вказане правило додавання векторів називають правилом трикутника. Це правило можна сформулювати так: для будь-яких трьох точок A, B і C
(мал. 5). Помітимо, що для знаходження двох неколінеарних векторів доводиться будувати трикутник. Тому вказане правило додавання векторів називають правилом трикутника. Це правило можна сформулювати так: для будь-яких трьох точок A, B і C 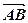 +
+ 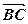 =
= 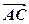 , або: сумою векторів
, або: сумою векторів  і
і  євектор
євектор 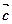 , який сполучає початок вектора
, який сполучає початок вектора  з кінцем вектора
з кінцем вектора  при умові, що вектор
при умові, що вектор  відкладено від кінця вектора
відкладено від кінця вектора  .
.
З цього правила випливає правило паралелограма: якщо вектори  і
і  відкладені від спільного початку O,
відкладені від спільного початку O, 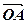 =
=  ,
, 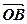 =
=  (мал. 6) і на них побудовано паралелограм OACB, то сумою векторів
(мал. 6) і на них побудовано паралелограм OACB, то сумою векторів  +
+  є вектор
є вектор 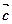 =
= 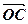 , який виходить з того ж початку і збігається з діагоналлю OC паралелограма.
, який виходить з того ж початку і збігається з діагоналлю OC паралелограма.
Розглянемо властивості операції додавання векторів.

Властивість 1. Операція додавання векторів комутативна, тобто для будь-яких векторів  і
і  :
:  +
+  =
=  +
+  .
.
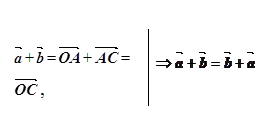 Доведення: За правилом трикутника маємо (мал. 7):
Доведення: За правилом трикутника маємо (мал. 7):
Властивість 2. Операція додавання векторів асоціативна, тобто для будь-яких векторів  ,
,  ,
, 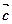 : (
: (  +
+  )+
)+ 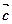 =
=  +(
+(  +
+ 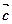 )
)
Доведення: Візьмемо довільну точку A і від неї відкладемо вектори 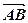 =
=  ,
, 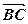 =
=  ,
, 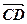 =
= 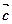 (мал. 8). Тоді
(мал. 8). Тоді  +
+  =
= 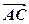 , (
, (  +
+  )+
)+ 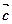 =
= 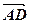 ;
;  +
+ 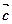 =
= 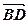 ;
;  +(
+(  +
+ 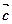 )=
)= 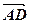 . Отже, (
. Отже, (  +
+  )+
)+ 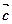 =
=  +(
+(  +
+ 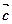 ).
).
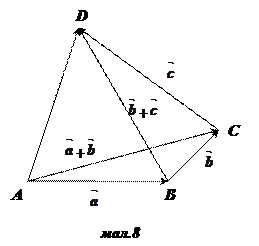
Властивість 3. Сумою протилежних векторів є нуль-вектор:  +(-
+(-  )=0.
)=0.
Доведення. Нехай  =
= 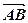 , тоді -
, тоді -  =
= 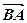 , і за правилом трикутника матимемо
, і за правилом трикутника матимемо  +(-
+(-  )=
)= 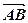 +
+ 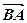 =
= 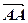 =0.
=0.
Властивість 4. Нуль-вектор є нейтральним елементом операції додавання:  +
+ 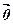 =
= 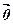 +
+  .
.
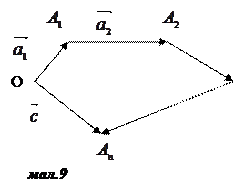
Доведення: Нехай  =
= 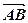 ,
, 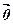 =
= 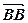 , тоді за правилом трикутника
, тоді за правилом трикутника  +
+ 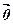 =
= 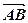 +
+ 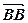 =
= 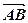 =
=  .
.
З наведених властивостей додавання векторів випливає, що операція додавання векторів має ті ж властивості, що й операція додавання чисел. Тому часто при перетворенні сум векторів діємо так само, як і при перетворенні числових виразів: (  +
+  )+
)+ 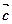 =
=  +(
+(  +
+ 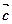 )=(
)=(  +
+ 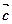 )+
)+  =
=  (
( 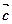 +
+  ).
).
Сума більшої кількості векторів знаходиться за правилом многокутника. Щоб знайти суму n векторів 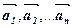 (мал. 9), потрібно з довільної точки O відкласти вектор
(мал. 9), потрібно з довільної точки O відкласти вектор 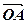 =
= 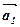 , з його кінця – вектор
, з його кінця – вектор 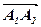 =
= 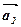 ,…,
,…, 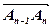 =
= 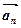 (початок кожного наступного вектора-доданка є кінцем попереднього). Вектор
(початок кожного наступного вектора-доданка є кінцем попереднього). Вектор 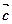 =
= 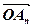 буде сумою даних векторів.
буде сумою даних векторів.








