Аппроксимация и интерполяция данных

Дата: 2025-06-02; Просмотры: 6
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

ЛАБОРАТОРНАЯ РАБОТА № 7

 

Аппроксимация и интерполяция данных

Цель работы: изучение методов сглаживания данных в среде MathCa d и получение соответствующих навыков вычислений.

 

ВВЕДЕНИЕ

При экспериментальном изучении различных эффектов и явлений часто сталкиваются с необходимостью функционального представления зависимостей, полученных в процессе измерений. С этой целью используют аппроксимацию и интерполяцию. Аппроксимация представляет собой сглаживание данных кривой, не проходящей в общем случае через экспериментальные точки, но отслеживающей зависимость, устраняя возможные ошибки, вызванные погрешность измерений. При интерполяции рассчитывают сглаживающую кривую, проходящую через каждую экспериментальную точку.

Задача 7

 

Дана таблица экспериментальных данных, зарегистрированных с погрешностью. Необходимо рассчитать уравнение кривой, сглаживающей данные и отражающей собой ход зависимости.

f(xi) 1.8 2.08 2.15 2.19 2.2 2.21 2.21 2.22 2.22 2.23 2.23 2.24 2.25
xi 0.01 0.125 0.25 0.5 0.75 1 1.3 1.5 1.75 2 2.25 2.5 2.75

 

Ввиду того, что экспериментальные данные получены с погрешностью, нет необходимости использовать интерполяцию (рассчитывать функцию, проходящую через каждую точку). В нашем случае необходимо провести аппроксимирующую кривую, которая не проходит через экспериментальные точки, но в то же время отражает исследуемую зависимость, сглаживает возможные выбросы за счет погрешности эксперимента.

Обозначим узлы (экспериментальные значения) исходной таблицы данных через xi, где 0 £ i £ n-1 - номер узла. Считаем известными значения экспериментальных данных в узловых точках f(xi) = fi . Введем непрерывную функцию j(x) для аппроксимации дискретной зависимости f(xi). В узлах функции f(x) и j(x) будут отличатся на величину

ei = j(xi) - f(xi). (1)

Отклонения ei могут принимать положительные и отрицательные значения. Чтобы не учитывать знаки, возведем каждое отклонение в квадрат и просуммируем квадраты отклонений по всем узлам

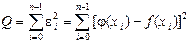. (2)

Метод построения аппроксимирующей функции j(x) из условия минимума величины Q называется методом наименьших квадратов (МНК).

Наиболее распространен способ выбора функции j(x) в виде линейной комбинации

j(x) = cojo(x) + c1j1(x) +...+ cmjm(x), (3)

где jo(x), j1(x), ... , jm(x) - базисные функции; m £ n; co, c1, ... , cm - коэффициенты, определяемые из условия минимума величины Q.

Математически условия минимума суммы квадратов отклонений Q запишем приравнивая к нулю частные производные от Q по коэффициентам ck, 0 £ k £ m;

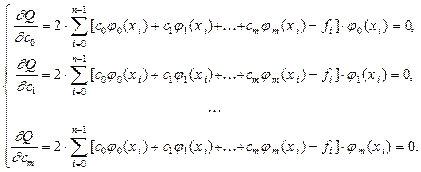(4)

Из системы линейных алгебраических уравнений (4) определяются все коэффициенты ck. Данная система называется системой нормальных уравнений. Матрица этой системы имеет следующий вид:

А = 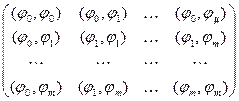(5)

и называется матрицей Грама. Элементы матрицы Грама являются скалярными произведениями базисных функций

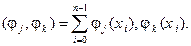(6) В = (7)

— матрица столбец свободных членов, где скалярные произведения определяются аналогично

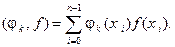(8)

Далее следует отметить основные свойства матрицы Грама, полезные при программной реализации алгоритмов МНК:

1. Матрица симметрична, т. е. аij=aji.

2. Матрица является положительно определенной

3. Определитель матрицы будет отличен от 0 если в качестве базиса выбраны линейно независимые функции jk(x), при этом система (4) имеет единственное решение.

При обработке экспериментальных данных, определенных с погрешностью e в каждой узловой точке, обычно начинают с аппроксимации функцией j(x), представимой одной - двумя базисными функциями. После коэффициентов ck вычисляют величину Q по формуле (2). Если получится что 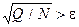, то необходимо расширить базис добавлением новых функций jk(x). Расширение базиса необходимо производить до тех пор, пока не выполняются условия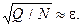

Выбор конкретных базисных функций зависит от свойств аппроксимируемой функции f(x), таких как периодичность, экспоненциальный или логарифмический характер, свойства симметрии, наличие асимптотики и т. д.

 

Степенной базис

Выберем базисные функции jk(x) в виде последовательности степеней аргумента x, которые линейно независимы.

jо(x) = x o= 1, j1(x) = x1 = x, ... , jm(x)=xm. (9)

Экспериментальную зависимость будем аппроксимировать полиномом. Степень полинома m выбираем обычно m << n.

Аппроксимирующая кривая в МНК не проходит через значения исходной функции в узлах, но проведена из условия наименьшего суммарного квадратичного отклонения. Если же выбрать m = n, то на основании единственности интерполяционного полинома получим функцию j(x), совпадающую с каноническим интерполяционным полиномом степени n. Аппроксимирующая кривая в этом случае пройдет через все экспериментальные точки и величина Q будет равна 0. Последнее обстоятельство используется для отладки и тестирования программ, реализующих алгоритмы МНК. Запишем матрицу Грама системы нормальных уравнений для базиса

 

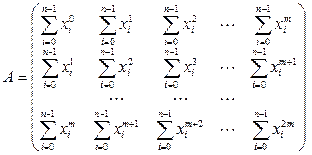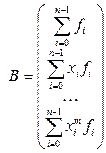(10) (11)

 

Программу аппроксимации будем писать используя степенной базис и реализуя следующие задания:

1. Ввод данных: таблицы X(N) и Y(N).

2. Формирование матрицы Грама и матрицы столбца свободных членов.

3. Решение системы нормальных уравнений.

4. Вычисление аппроксимирующей функции.

5. Вывод результатов расчетов (экспериментальные точки и рассчитанная кривая).

Естественно, что для практического использования необходима программа, которая позволяет: 1) достаточно простым способом изменять степень полинома, аппроксимирующего зависимость; 2) данные, подлежащие аппроксимации считывать из внешнего файла; 3) быть простой, понятной и достаточно универсальной. Ниже приведен MathCad - документ решения задачи аппроксимации с учетом указанных требований.

 

MathCad программа решения задачи 7

 

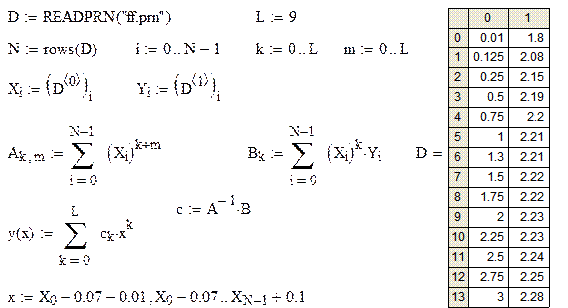
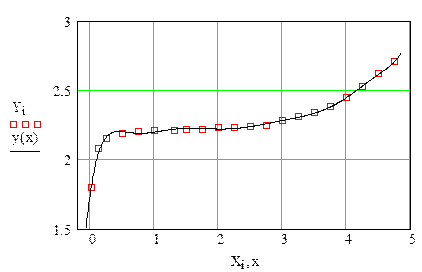
Приведённая программа аппроксимирует экспериментальную зависимость полиномом степени L. Пользователь задаёт значение величины L исходя из результатов сглаживания.

Следует отметить, что система MathCad содержит функции, позволяющие выполнять аппроксимацию. Функция intercept( X, Y) вычисляет коэффициент а линейной регрессии y = a + b.x векторов X и Y. Функция slope( X, Y) вычисляет коэффициент b линейной регрессии y = a + b.x векторов X и Y. Сглаживание экспериментальных данных можно выполнить с помощью функции ksmooth( X, Y, b), которая рассчитает усредненные значения величин Y, определенные на основе распределения Гаусса. X и Y - векторы действительных чисел. Величина b задает полосу пропускания, управляющую сглаживанием.

Функция interp( Vs, X, Y, x) возвращает значение сплайна в точке x, вычисленное по исходным векторам X и Y и коэффициентам сплайна Vs. Vs := loess( X, Y, okr) - вектор, используемый функцией interp, okr - размер области аппроксимации.

Аппроксимацию данных по МНК выполняет функция linfit( X, Y, j), здесь j - символьный вектор базисных функций. Использование функции linfit существенно упрощает MathCad - документ и позволяет пользователю самостоятельно задавать набор базисных функций. Приведем MathCad - документ решения задачи аппроксимации с использованием функции linfit.

 

MathCad программа решения задачи 7 (с помощью функции linfit)

 

 

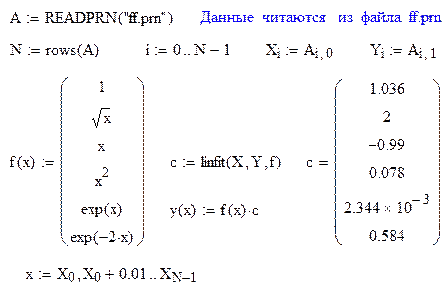
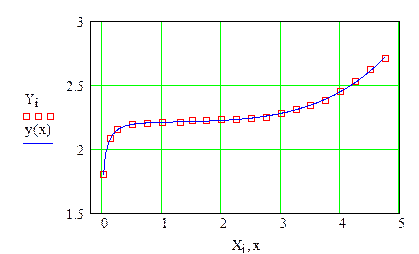
Просмотрев результат работы функции linfit, при неудовлетворительном сглаживании пользователь может увеличить число базисных функций или видоизменить одну из них или несколько, пока не получит удовлетворительный результат. Насколько существенным является вклад каждой из базисных функций показывает величина коэффициентов Ск.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

 

  1. Что такое аппроксимация данных?
  2. В чем состоит принцип аппроксимации по МНК?
  3. В каком виде задают функцию аппроксимирующую данные по МНК?
  4. Напишите и поясните аргументы функции linfit.
  5. От чего зависит выбор базисных функций?
  6. Что такое интерполяция данных?
  7. Как выглядит символьный вектор базисных функций для степенного базиса?
  8. Чем ограничено количество используемых в программе аппроксимации базисных функций?

 

 

литература

1. Очков В.Ф. Mathcad PLUS 6.0. для студентов и инженеров. - М.: ТОО фирма “Компьютер Пресс”, 1996 г. - 238 с.

2. А. Е. Мудров Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. – Томск: МП «РАСКО», 1991. 272 с.

3. М. Херхагер, Х. Партолль MathCad 2000 : полное руководство. Пер. с нем. - К. : Издательская группа BHV, 2000, - 416 с.

4. Дьяконов В.П., Абраменкова И.В. MathCad 7.0 в математике, физике и в Internet. - М.: «Нолидж», 1999. - 352 с.

5. Очков В.Ф. Mathcad 7 PRO для студентов и инженеров. - М.: “Компьютер Пресс”, 1998 г. - 384 с.

6. Кирьянов Д.В. Самоучитель MathCad 11. – СПб.: БХВ – Петербург, 2003.

7. Макаров Е. Г. Инженерные расчеты в MathCad Учебный курс. – СПб.: Питер. 2005. – 448 с.