Простейший метод численного решения дифференциальных уравнений

Дата: 2025-06-02; Просмотры: 8
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

ЛАБОРАТОРНАЯ РАБОТА № 5

 

Простейший метод численного решения
дифференциальных уравнений

Цель работы: изучение простейшего метода решения дифференциальных уравнений в среде MathCa d и получение соответствующих навыков вычислений с использованием матриц.

 

ВВЕДЕНИЕ

 

Большое количество задач сводится к решению дифференциальных уравнений, однако, лишь небольшая часть их может быть решена аналитически. В связи с этим значительно возрастает роль численного решения дифференциальных уравнений.

Дифференциальным называется уравнение относительно неизвестной функции и её производных различных порядков 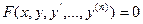. Рассмотрим задачу 5.

Задача 5

 

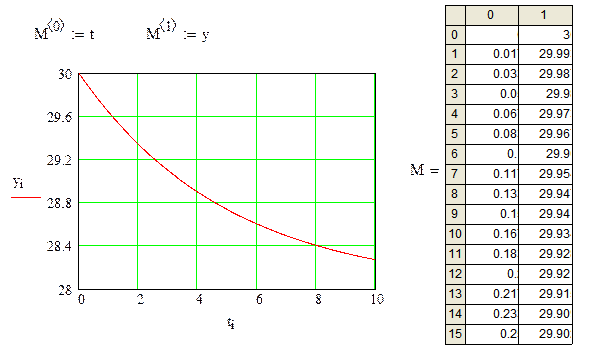
Изменение некоторой величины y( t) описывается уравнением 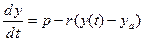. (1) Вычислить y( t) в диапазоне изменения t от 0 до10, если р = 2, r = 0.2, ya = 18. Начальное значение y(0) = 30.

 

Даже в том случае, когда аналитическое решение данного уравнения все же существует, необходимо представить решение в графическом виде, чтобы понять его характер. В связи с этим, необходимо найти численное решение уравнения (1).

 

Алгоритм Эйлера.

Метод численного решения диф. уравнений включает в себя преобразование диффуравнения в уравнение конечноразностное. Поскольку уравнение (1) описывает изменение величины y(t), то с известной степенью точности можно записать

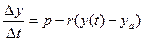, где 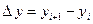, а Dt - конечный интервал, т. е. 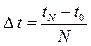(2). С учетом этого из уравнения (3) получим:

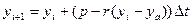(3).

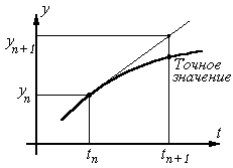
Это и есть конечноразностное уравнение, соответствующее дифференциальному уравнению (1). В первом приближении предполагается, что правая часть уравнения (1), т. е. скорость изменения y постоянна на отрезке Dt. Это метод касательных или метод Эйлера. Совершенно очевидно, что данный метод будет давать хорошее приближение, если Dt достаточно мало. Сформулируем данный метод в виде алгоритма для компьютера:

1. Задаются величина шага, количество итераций и начальные условия.

2. Создается блок вычислений с помощью матриц, содержащий итерационные формулы.

3. Графически представляются результаты вычислений.

 

MathCad программа решения задачи 5

 

 

 

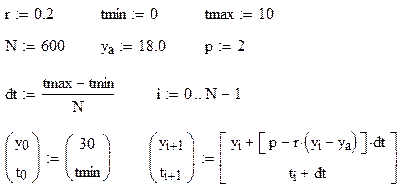
При решении такого типа задач часто сталкиваются с необходимостью определить влияние на полученное решение какого либо изменяющегося параметра. Для этого необходимо задать вектор, соответствующий изменению параметра и рассчитывать уже набор векторов решения, т.е. матрицу решения. Принцип реализации таких вычислений приведён в следующей MathCad программе.

 

MathCad программа решения задачи 5 m

 

 

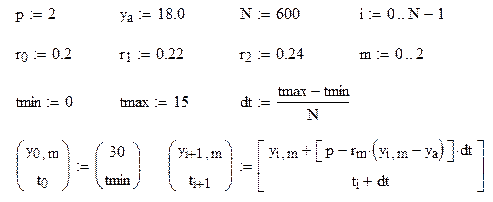
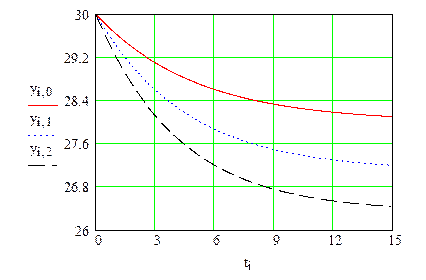
На графике представлены три зависимости, соответствующие трём значениям параметра r. Увеличение r приводит к более сильному уменьшению рассчитываемой величины.

Естественно, что численное решение не может точно совпадать с “истинным” исходного дифференциального уравнения (погрешность результата порядка dt). В общем случае отклонение от точного решения обусловлено двумя причинами. В компьютере вещественные числа представляются некоторым конечным числом десятичных цифр. Погрешность, связанная с представлением вещественных чисел в компьютере, ограничиваясь заданным количеством цифр после точки (например, 15) называется погрешностью округления. Важность погрешностей округления заключается в том, что они накапливаются по мере роста вычислений.

Другой источник отклонения численного решения от точного обусловлен выбором алгоритма вычислений. Это погрешность приближения. Однако, у каждого метода решения дифференциальных уравнений имеются свои достоинства и недостатки, а соответствующий выбор определяется нашими требованиями и характером конкретного решения.

Практически точность численного решения определяют, уменьшая величину шага Dt до тех пор, пока численное решение не перестанет зависеть от шага при требуемом уровне точности.

Наряду с точностью алгоритма, другой важной характеристикой представляется его устойчивость. Например, может случится так, что численные результаты находятся в хорошем соответствии с “истинным” решением на малых временах, а на больших временах отклоняются от него. Такое отклонение может происходить из-за того что малые погрешности в алгоритме решения задачи накапливаются и приводят к геометрическому росту погрешности. Для конкретных задач такой алгоритм называется неустойчивым.

 

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

 

  1. Как получить конечноразностное уравнение, соответствующее данному дифференциальному уравнению?
  2. В чем состоит сущность простейшего метода численного решения диффуравнения (метода Эйлера)?
  3. С чем связано наличие погрешностей вычислений?
  4. Какие типы погрешностей вычислений Вы знаете?
  5. Как может пользователь уменьшить погрешность приближения?
  6. Поясните сущность неустойчивого алгоритма решения задачи?
  7. Как объединить два столбца данных одинакового размера в матрицу?

 

литература

1. Гулд Х., Тобочник Я. Компьютерное моделирование в физике: в 2-х частях. Пер. с англ. - М.:Мир, 1990 г.

2. А. Е. Мудров Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. – Томск: МП «РАСКО», 1991. 272 с.

3. М. Херхагер, Х. Партолль MathCad 2000 : полное руководство. Пер. с нем. - К. : Издательская группа BHV, 2000, - 416 с.

4. Дьяконов В.П., Абраменкова И.В. MathCad 7.0 в математике, физике и в Internet. - М.: «Нолидж», 1999. - 352 с.

5. Очков В.Ф. Mathcad 7 PRO для студентов и инженеров. - М.: “Компьютер Пресс”, 1998 г. - 384 с.

6. Бородич Л.И., Герасимович А.И., Кеда Н.П., Мелешко И.Н. Справочное пособие по приближенным методам решения задач высшей математики. - Мн.: Высшая школа, 1986. - 189 с.

7. Кирьянов Д.В. Самоучитель MathCad 11. – СПб.: БХВ – Петербург, 2003.

8. Шушкевич Г.Ч., Шушкевич С.В. Введение в MathCad 2000 : Учебное пособие. – Гродно: ГрГУ, 2001. – 140 с.