Зависимости, описываемые функциями двух переменных
ЛАБОРАТОРНАЯ РАБОТА № 4
Зависимости, описываемые функциями двух переменных
Цель работы: изучение методов исследования зависимостей двух переменных в среде MathCa d и получение соответствующих навыков вычислений и графического представления результатов.
ВВЕДЕНИЕ
Зависимости от двух переменных достаточно часто встречаются при исследовании различных процессов, поэтому их изучение актуально. Простейший путь исследования таких зависимостей состоит в фиксировании значения одной переменной с дальнейшим изучением поведения уже функции одной переменной с использованием декартовой графики.
Наличие в MathCad трехмерной графики (3D – графики) дает специальные возможности в исследовании сложных зависимостей. Зависимость от двух переменных можно представить в виде поверхности, контурного графика (линий уровня), графика векторное поле, либо в виде трехмерной столбчатой диаграммы.
Чтобы использовать указанную графику, необходимо, исходя из заданной функциональной зависимости, рассчитать матрицу данных, которые будут представлены с использованием одного из трех указанных типов графики.
Отмеченное выше может быть продемонстрировано на примере решения задачи 7.
Задача 4
Графически представить зависимость, заданную функцией двух переменных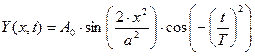 
. Переменная x изменяется в диапазоне от - а до а, а t – в диапазоне от 3Т до 5Т. А0 = 1, а = 0.02, Т = 2.7 .
Для решения задачи 4 необходимо:
1. Задать значения параметров (А0, а, Т), необходимые для определения функции пользователя Y(x,t).
2. Создать функцию пользователя Y(x,t).
3. Задать параметры диапазонов вычислений.
4. Создать вектора, соответствующие переменным x и t.
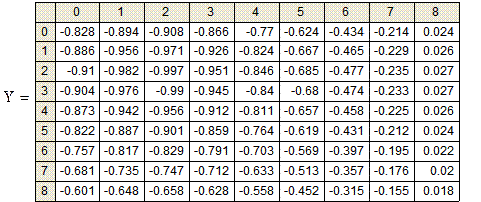
5. Вычислить матрицу данных Yn,m.
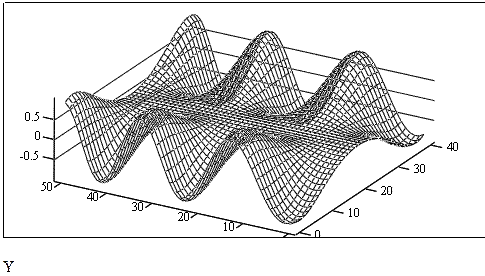
6. Результаты представить в виде графика «поверхность».
MathCad программа решения задачи 4
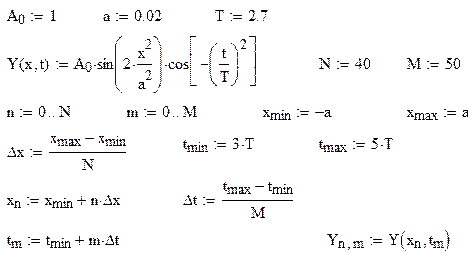
Альтернативный предложенному метод вычислений при анализе функциональных зависимостей – непосредственное вычисление векторов и матриц без задания функций пользователя. Применительно к данной задаче, не задавая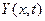 
, следовало рассчитать Yn,m :
.
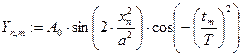В среде MathCad 2001 i имеется функция создания матрицы для графика трехмерной поверхности - CreateMesh(F(или g, или f1, f2, f3), s0, s1, t0, t1, Ns, Nt, fmap) – производит расчёт вложенного массива, представляющего х-, у- и z-координаты параметрической поверхности, заданной функцией F; где F(s,t) - векторная функция из трех элементов, заданная параметрически относительно двух аргументов s и t; g(s,t) - скалярная функция; fl(s,t) ,f2(s,t) ,f3(s,t) - скалярные функции;
s0,t0 - нижние пределы аргументов s,t (по умолчанию -5);
s1,t1 - верхние пределы аргументов s,t (по умолчанию 5);
Ns, Nt - число точек сетки по переменным s и t (по умолчанию 20);
fmap - векторная функция от трех аргументов, задающая преобразование координат. Аргумент fmap является необязательным. Пример использования функции CreateMesh приведён ниже.
MathCad программа решения задачи 4(с использованием функции CreateMesh).
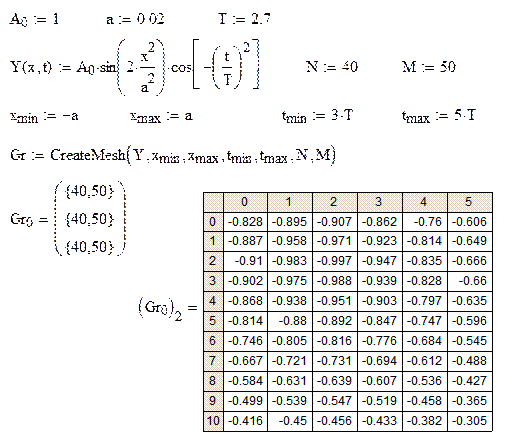
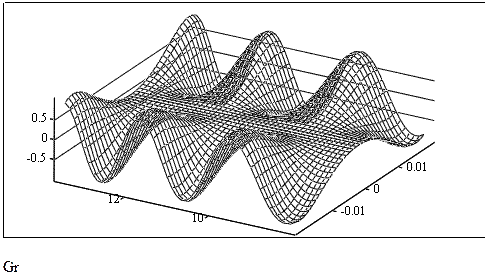
Использование функции CreateMesh позволяет существенно автоматизировать процесс построения поверхности.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Перечислите типы графиков, которые используются в MathCad для визуализации результатов.
2. Выведите на экран содержимое матрицы результатов вычислений.
3. Выведите на экран содержимое 5-й строки матрицы Y.
4. Выведите на экран содержимое обьекта Gr.
5. Выведите на экран содержимое 10-го столбца матрицы Y.
6. Перечислите аргументы функции CreateMesh и их назначение.
7.
литература
1. Очков В.Ф. Mathcad PLUS 6.0. для студентов и инженеров. - М.: ТОО фирма “Компьютер Пресс”, 1996 г. - 238 с.
2. Гулд Х., Тобочник Я. Компьютерное моделирование в физике: в 2-х частях. Пер. с англ. - М.:Мир, 1990 г.
3. А. Е. Мудров Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. – Томск: МП «РАСКО», 1991. 272 с.
4. М. Херхагер, Х. Партолль MathCad 2000 : полное руководство. Пер. с нем. - К. : Издательская группа BHV, 2000, - 416 с.
5. Дьяконов В.П., Абраменкова И.В. MathCad 7.0 в математике, физике и в Internet. - М.: «Нолидж», 1999. - 352 с.
6. Очков В.Ф. Mathcad 7 PRO для студентов и инженеров. - М.: “Компьютер Пресс”, 1998 г. - 384 с.
7. Бородич Л.И., Герасимович А.И., Кеда Н.П., Мелешко И.Н. Справочное пособие по приближенным методам решения задач высшей математики. - Мн.: Высшая школа, 1986. - 189 с.
8. Кирьянов Д.В. Самоучитель MathCad 11. – СПб.: БХВ – Петербург, 2003.
9. Макаров Е. Г. Инженерные расчеты в MathCad Учебный курс. – СПб.: Питер. 2005. – 448 с.
10. Шушкевич Г.Ч., Шушкевич С.В. Введение в MathCad 2000 : Учебное пособие. – Гродно: ГрГУ, 2001. – 140 с.