Контрольная работа «Определенный интеграл»
Компьютерная версия: Попов А.
Вариант №1
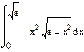1. Вычислить интегралы:
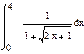
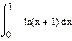
а) б) в)
2. Найти среднеее значение функции f ( x )= x 2 на отрезке [0,1]
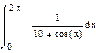
3. Дать оценку интеграла
4. Вычислить площадь фигуры, ограниченной линиями x =-2 y 2 , x =1-3 y 2
5. Вычислить площадь фигуры, лежащей вне круга ρ=α и ограниченной
кривой ρ=2α∙ cos 3 φ
6. Вычислить объем тела, образованного вращением фигуры,
ограниченной линиями ( y -1)2= x , y =2, x =0
а) вокруг оси OY;
б) вокруг оси OX.
7. Вычислить длину одной арки циклоиды x = a ∙( t - sint )
y=α∙(1-cost)
Вариант №2
1. 
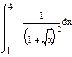Вычислить интегралы:
 |
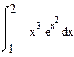а) б) в)
2. Найти среднее значение функции f ( x )= sin 2 x на отрезке
[0,π]
 |
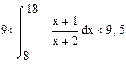3. Доказать неравенство
4. Вычислить площадь, заключенную между параболой
y =- x 2 -2 x +3, касательной к ней в точке M(2,-5) и осью ординат
5. Вычислить площадь фигуры, ограниченной окружностью
ρ=α, кардиоидой ρ=α (1- cosφ ) и содержащей точку M с
прямоугольными координатами (α/2,0)
6. Вычислить объем тела, образованного вращением фигуры, ограниченной линиями y = sinx , x=π/2, y =0
а) вокруг оси OX;
б) вокруг оси OY.
7. Вычислить длину астроиды x = a ∙ cos 3 t
y = a ∙ sin 3 t
Вариант №3
1. Вычислить интегралы:
 |  | ||||
 | |||||
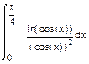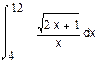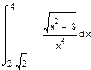а) б) в)
2. Найти среднее значение функции f(x)=a+b∙cosx на отрезке [-π,π]
 |
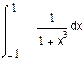3. Дать оценку
4. Найти площадь фигуры, ограниченной линиями y 2 =10 x +25,
y 2 =-6 x +9
5. Найти площадь одного лепестка кривой ρ=4∙ sin 2 φ
6. Найти объем тела, образованного вращением фигуры,
ограниченной полукубической параболой y 2 = x 3, осью OX и прямой x =1
а) вокруг оси OX;
б) вокруг оси OY.
7. Вычислить длину дуги кривой x =( t 2 -2)∙ sint +2 t ∙ cost , y =(2- t 2 )∙ cost +2 t ∙ sint,
заключенной между точками, соответствующими значением параметра t1=0, t2=π
Вариант №4
1. Вычислить интегралы:
 |  | ||||
 | |||||
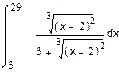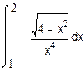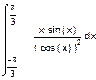а) б) в)
2. Найти среднее значение функции f ( x )=3 x 2 +2 x -1 на отрезке
[1,5]
 |
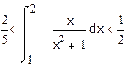3. Доказать неравенство
4. Найти площадь фигуры, лежащей выше оси OX и
ограниченной линиями: y 2 =4 x , y =2 x -4
5. Найти площадь части фигуры, ограниченной лемнискатой
Бернулли ρ2=α2∙ cos 2 φ, лежащей внутри окружности ρ=α./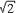 
6. Вычислить объем тела, образованного вращением фигуры,
ограниченной линиями x 2 - y 2 = a 2 , x =+-2 a
a) вокруг оси OX;
б) вокруг оси OY.
7. Вычислить длину дуги кривой x = et ∙ cost , y = et ∙ sint, заключенной между точками, соответстующими значениям параметра t1=0, t2=π
Вариант №5
1. Вычислить интегралы:
 | |||||
 | |||||
 | |||||
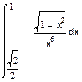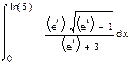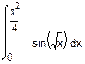а) б) в)
2. Найти среднее значение функции f ( x )= cos 3 x на отрезке [o,π]
 |
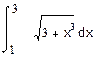3. Дать оценку
4. Найти площадь фигуры, заключенной между параболами y =4 x 2,
y = x 2 /9 и прямой y =2
5. Вычислить площадь четырехлепестковой розы ρ=α∙sin2φ
6. Вычислить объем тела, образованного вращением фигуры,
ограниченной линиями y = x 2 +1, x =-1, y =0
a) вокруг оси OX;
б) вокруг оси OY.
7. Вычислить длину дуги кривой x =8 at 3 , y =3 a (2 t 2 - t 4 ), заключенной
между точками, соответствующими значениям параметра t1=0, t2=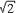
Вариант №6
1. Вычислить интегралы:
 |  | ||||
 | |||||
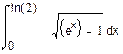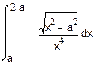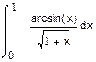a) б) в)
2. Найти среднее значение функции f ( x )=10+2 sinx +3 cosx на
отрезке [o,2π]
 |
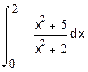3. Дать оценку
4. Найти площадь фигуры, заключенной между линиями y =2 x,
y+2=2x, x=0, y=2
5. Найти площадь фигуры, ограниченной кривыми ρ=2cosφ,
ρ=1 (вне круга ρ=1)
6. Вычислить объем тела, образованного вращением фигуры,
ограниченной линиями x 2 + y 2 =1, y =0, y =(1.5 x )1/2
a) вокруг оси OX;
б) вокруг оси OY.
7. Вычислить длину дуги кривой x=8sinx+6cosx, y=6sinx-8cosx,
заключенной между точками, соответствующими значениям параметра t1=0, t2=π/2
Вариант №7
1. Вычислить интегралы:
 | |||||
 | |||||
 | |||||
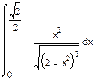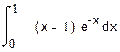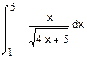а) б) в)
2. Найти среднее значение функции f ( x )=3 x -2 x +3 на отрезке [o,2]
 |
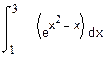3. Оценить интеграл
4. Найти площадь фигуры, заключенной между линиями y = x 3 , y = x ,
y=2x (x>0)
5. Вычислить площадь фигуры, ограниченной окружностью ρ=α,
кардиоидой ρ=α∙(1- cos φ) и содержащей точку M(-α/2,0)
6. Вычислить объем тела, образованного вращением фигуры,
ограниченной линиями x 2 - y 2 =4, y =+-2, x =0
а) вокруг оси OY;
б) вокруг оси OX.
7. Вычислить длину дуги полукубической параболы x = t 2 , y =2 t 3 /3,
заключенной между точками, соответствующими значениям
параметра t1=0, t2=2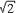
Вариант № 8
1. 1. Вычислить интегралы:
 |  |  | |||
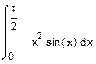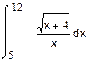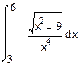а) б) в)
 |
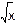2. Найти среднее значение функции f ( x )= на отрезке [0,100]
 |
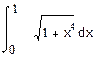3. Оценить интеграл
4. Найти площадь фигуры, заключенной между линиями x = y 2 ,
x =3 y2/4+1
6. 5. Вычислить площадь фигуры, ограниченной окружностью ρ=α,
7. кардиоидой ρ=α∙(1- cos φ) и содержащей точку M(-3α/2,0)
6. 6. Вычислить объем тела, образованного вращением фигуры,
ограниченной линиями y = ex , x =0, x =2
а) вокруг оси OY;
б) вокруг оси OX.
8. 7. Вычислить длину дуги логарифмической спирали x = et ∙ sint ,
y = et ∙ cost , заключенной между точками, соответствующими
значениям параметра t1=0, t2=π/2