Статистический анализ уравнения регрессии
Экономические данные формируются под действием множества факторов, не все из которых доступны внешнему контролю. Стохастическая (случайная) природа экономических данных обуславливает необходимость применения специальных статистических методов для анализа. Для выявления взаимосвязей между выборками используют методы исследования корреляционного анализа.
Корреляция (от латинского - взаимосвязь, отношение) – это понятие, с помощью которого определяют связь между явлениями.
Знание взаимосвязей отдельных признаков дает возможность предвидеть, прогнозировать развитие ситуации при изменении характеристик объекта исследования.
Обычно связь между выборками носит не строго функциональный, а вероятностный (стохастический) характер. Корреляционный анализ определяет степень связи между случайными величинами, а регрессионный анализ устанавливает форму зависимости между ними.
Из курсов ТВ и МС известно, что существуют зависимые и независимые случайные величины. Степень зависимости можно оценить с помощью корреляционного момента, т.е. математического ожидания произведения центрированных случайных величин Х и У. Эта величина называется ковариацией и обозначается СО V ( X ; Y ).
СО V ( X ; Y ) = М(Х-М(Х))(У-М(У)) =
= М(ХУ) – М(Х)М(У).
Для независимых случайных величин Х и У М(ХУ) = М(Х)М(У),
поэтому СО V ( X ; Y ) = 0 .
Выборочный аналог – выборочная ковариация численно равна разности выборочного среднего произведений случайных величин и произведения их выборочных средних. Недостаток данной характеристики - зависимость от единиц измерения изучаемых величин. Так, если одна из величин имеет малое рассеяние, то ковариация мала даже при тесной связи. Поэтому в расчетах так же используется нормированную величину ковариации - коэффициент корреляции.
Для оценки линейной зависимости между двумя параметрами применяют парный коэффициент линейной корреляции Пирсона (r).
r = СО V ( X ; Y ) / (σ(Х)σ(У)).
Типы зависимостей и значение коэффициента корреляции:
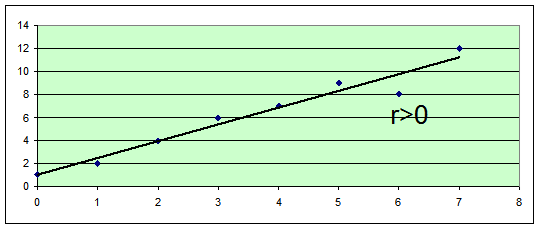
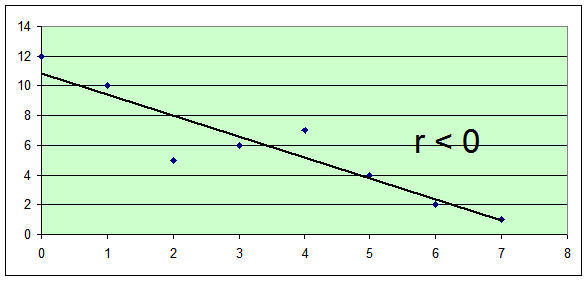

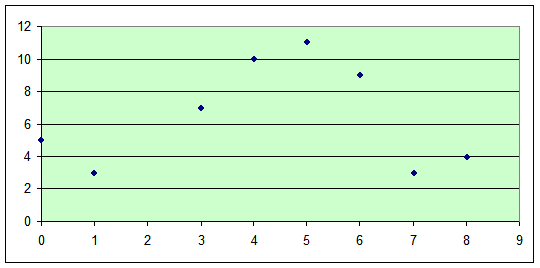
r = 0
В 1-м случае связь между величинами является прямой, во 2-м – обратной, в 3-м случае близость нулю коэффициента корреляции свидетельствует об отсутствии линейной взаимосвязи, а не об отсутствии связи вообще.
Для характеристики степени (тесноты) связи между величинами используют различные эмпирические правила. Например, если
׀r׀ > 0,95, то существующая связь практически линейная;
если 0,8 < ׀r׀ < 0,95 , то говорят о наличие сильной линейной зависимости, при 0,6 < ׀r׀ < 0,8 - о наличие линейной зависимости; при ׀r׀ < 0,4
считают, что линейную взаимосвязь выявить не удалось.
В среде MS Excel для вычисления парных коэффициентов линейной корреляции используется функция КОРРЕЛ.
Для оценки общего качества оцениваемой линейной регрессии используют коэффициент детерминации R2 , называемый квадратом множественной корреляции. Для случая парной регрессии он совпадает с квадратом линейного коэффициента корреляции: R 2 = r 2
Коэффициент R2 можно интерпретировать как меру эффективности модели. При R 2 > 0,95 считают, что модель хорошо описывает данные, при R 2 < 0,6 – модель требует улучшения.








