«Прикладная математика»
Санкт-Петербургский государственный экономический университет
Институт сервиса
Факультет сервиса автотранспорта и бытовой техники
Кафедра прикладной математики и эконометрики
Контрольная работа для студентов
«Прикладная математика»
Составитель: доцент А.В. Гармашов
СПб 2013
ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Решить графическим методом задачи с двумя переменными (табл. 1).
Таблица 1. Варианты задания 1
| Вариант | Задача | Вариант | Задача |
| 1 | 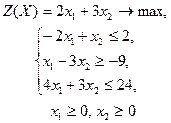
| 16 | 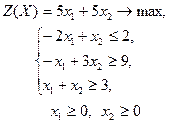
|
| 2 | 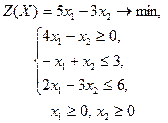
| 17 | 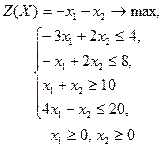
|
| 3 | 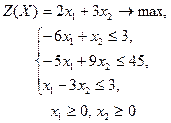
| 18 | 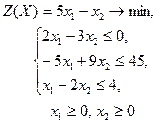
|
| 4 | 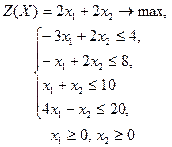
| 19 | 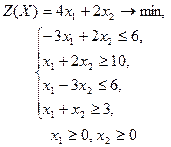
|
| 5 | 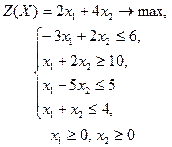
| 20 | 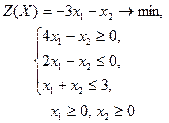
|
| 6 | 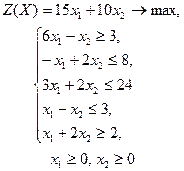
| 21 | 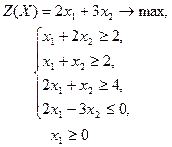
|
| 7 | 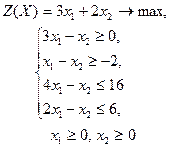
| 22 | 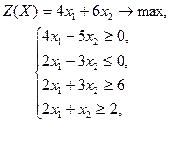
|
| 8 | 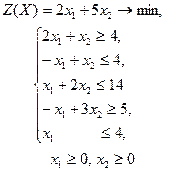
| 23 | 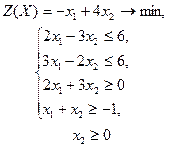
|
| 9 | 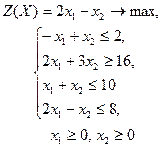
| 24 | 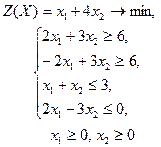
|
| 10 | 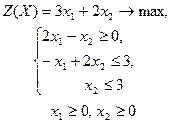
| 25 | 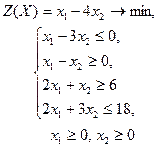
|
| 11 | 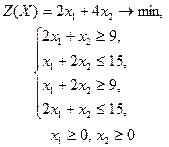
| 26 | 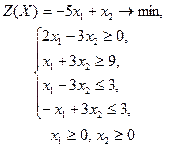
|
| 12 | 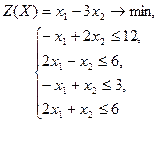
| 27 | 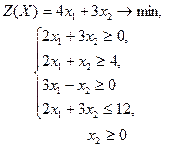
|
| 13 | 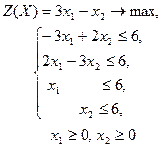
| 28 | 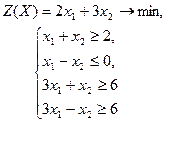
|
| 14 | 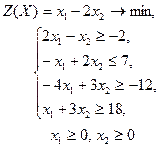
| 29 | 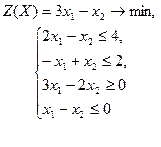
|
| 15 | 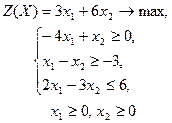
| 30 | 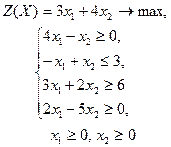
|
Формулирование задач линейного программирования для последующего их решения симплекс-методом
Следующие задачи сформулировать как задачи линейного программирования и решить их симплекс-методом.
1-7. На предприятии имеется возможность выпускать три вида продукции П j 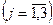 . При её изготовлении используются ресурсы Р1, Р2 и Р3. Размеры допустимых затрат ресурсов ограничены соответственно величинами b 1 , b 2 и b 3 . Расход ресурса i-го
. При её изготовлении используются ресурсы Р1, Р2 и Р3. Размеры допустимых затрат ресурсов ограничены соответственно величинами b 1 , b 2 и b 3 . Расход ресурса i-го 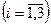 вида на единицу продукции j-го вида составляет aij единиц. Цена единицы продукции j-го вида равна cj ден. ед. Требуется симплекс-методом найти план выпуска продукции по видам с учётом имеющихся ограниченных ресурсов, который обеспечивал бы предприятию максимальный доход.
вида на единицу продукции j-го вида составляет aij единиц. Цена единицы продукции j-го вида равна cj ден. ед. Требуется симплекс-методом найти план выпуска продукции по видам с учётом имеющихся ограниченных ресурсов, который обеспечивал бы предприятию максимальный доход.
1. b1=150, b2=180, b3=120, a11=2, a12=3, a13=4, a21=1, a22=4, a23=5, a31=3, a32=4, a33=2, c1=8, c2=7, c3=6.
2. b1=1200, b2=150, b3=3000, a11=15, a12=20, a13=25, a21=2, a22=3, a23=2,5, a31=35, a32=60, a33=60, c1=300, c2=250, c3=450.
3. b1=600, b2=30, b3=144, a11=10, a12=20, a13=23, a21=1, a22=1, a23=1, a31=5, a32=6, a33=6, c1=35, c2=60, c3=63.
4. b1=24, b2=10, b3=6, a11=5, a12=7, a13=4, a21=5, a22=2, a23=1, a31=2, a32=1, a33=1, c1=18, c2=12, c3=8.
5. b1=500, b2=550, b3=200, a11=2, a12=1, a13=0, a21=0, a22=2, a23=1, a31=0, a32=1, a33=0, c1=3, c2=4, c3=1.
6. b1=360, b2=192, b3=180, a11=18, a12=15, a13=12, a21=6, a22=4, a23=8, a31=5, a32=3, a33=3, c1=9, c2=10, c3=16.
7. b1=180, b2=210, b3=244, a11=4, a12=2, a13=1, a21=3, a22=1, a23=3, a31=1, a32=2, a33=5, c1=10, c2=14, c3=12.
8. Производитель элементов центрального отопления изготовляет радиаторы четырёх моделей. Ограничения на производство обусловлены количеством рабочей силы и количеством стальных листов, из которых изготавливают радиаторы.
| Модель радиатора | А | В | С | D |
| Необходимое количество рабочей силы, человеко-часы | 0,5 | 1,5 | 2 | 1,5 |
| Необходимое количество стального листа, м2 | 4 | 2 | 6 | 8 |
| Прибыль от продажи одного радиатора, долл. | 5 | 5 | 12,5 | 10 |
Количество стального листа — не более 2500 м2, количество человеко-часов — не более 500. Решите эту задачу с максимизацией прибыли в качестве целевой функции.
9. Фирма производит три вида продукции (А, В, С), для выпуска каждого из которых требуется определённое время обработки на всех четырёх устройствах I, II, III, IV.
| Вид продукции | Время обработки | Прибыль, долл. | |||
| I | II | III | IV | ||
| А | 1 | 3 | 1 | 2 | 3 |
| В | 6 | 1 | 3 | 3 | 6 |
| С | 3 | 3 | 2 | 4 | 4 |
Пусть время работы на устройствах — соответственно 84,42, 21 и 42 часа. Определите, какую продукцию и в каких количествах следует производить. Рынок сбыта для каждого продукта неограничен. Временем, требуемым для переключения устройства в зависимости от вида продукции, можно пренебречь. Рассмотреть задачу максимизации прибыли.
10. Прибыль от изделий А, В, С составляет, соответственно, 3, 4, 5 единиц. Для каждого изделия требуется время использования станка I и II, которые доступны, соответственно, 12 и 15 часов в день:
| А | В | С | |
| I | 2 | 3 | 3 |
| II | 4 | 1 | 2 |
Найдите оптимальный план производства.
11. Постройте экономико-математическую модель для следующей ситуации. Фирма производит три вида продукции, используя для этого два вида ресурсов. Технологическая матрица задана в виде таблицы:
| Продукт 1 | Продукт 2 | Продукт 3 | |
| Ресурс 1 | 1 | 2 | 0 |
| Ресурс 2 | 2 | 3 | 1 |
Фирма имеет в своём распоряжении 20 единиц 1-го ресурса и 25 единиц 2-го ресурса; цены, по которым предполагает реализовать свою продукцию фирма, равны 15, 20, 30 тыс. руб. за 1-й, 2-й и 3-ий товар, соответственно. Фирма желает получить максимальный доход.
12. Фирма специализируется на производстве мебели для жилых помещений. Она может производить три типа мебельных гарнитуров A, B, C, что требует различных затрат труда на каждой стадии производства:
| Производственный участок | Затраты труда, чел-ч | ||
| A | B | C | |
| лесопилка | 1 | 2 | 4 |
| сборочный цех | 2 | 4 | 2 |
| отделочный цех | 1 | 1 | 2 |
В течение недели можно планировать работу на лесопилке на 360 чел-ч, в сборочном цехе – на 250 чел-ч, в отделочном цехе - на 220 чел-ч. Прибыль от продажи каждого типа гарнитуров A, B, C составляет, соответственно, 900, 1100 и 1500 долл. Определите производственную программу для получения максимальной прибыли.
13. Фирма производит на фабрике четыре сорта изделий. Производство лимитируется временем использования станков и количеством комплектующих изделий. Известно также, что суммарное время использования станков — 90 ч в день, а комплектующих изделий может бы поставлено не более 80 в день.
| Производственные характеристики | Изделие | |||
| 1 | 2 | 3 | 4 | |
| Время использования станка, ч | 1 | 3 | 8 | 4 |
| Количество комплектующих изделий | 2 | 2 | 1 | 3 |
| Себестоимость изделия, ден. ед. | 20 | 25 | 40 | 85 |
| Доход от продажи, ден. ед. | 30 | 45 | 80 | 45 |
Определите производственную программу для получения максимальной прибыли.
А. Фирма может увеличить время работы станков до 100 ч, при этом себестоимость каждого изделия всех четырёх видов увеличится на 10 ден. ед. Какова будет прибыль фирмы в этом случае? Изменится ли производственная программа?
Б. Беспорядки на заводе одного из потребителей приводят к тому, что дневной выпуск изделия 4 сокращён до 15 единиц. Как это повлияет на производственный план и размер прибыли фирмы?
14. Фирма, выпускающая трикотажные изделия, использует для производства продукции два вида сырья. Все необходимые данные приведены в таблице.
| Сырьё | Запас сырья, кг | Затраты на единицу продукции | ||
| свитер | пуловер | костюм 1 | ||
| Чистая шерсть | 160 | 0,4 | 0,2 | 0,8 |
| Силон | 60 | 0,2 | 0,1 | 0,2 |
| Прибыль за изделие, ден.ед. | 16 | 15 | 22 | |
Записать в математической форме условия выпуска готовой продукции и найти симплекс-методом оптимальный план выпуска готовой продукции, если сырьё расходуется полностью, а прибыль должна быть максимальной.
15. Компания производит различные типы мебели для кабинетов. Она производит столы трех типов (1,2, 3). Объём работы, необходимой для каждой операции, приводится в таблице:
| Операция | Объём работы, чел-ч | ||
| 1 | 2 | 3 | |
| Изготовление частей | 2 | 3 | 2 |
| Сборка | 1 | 2 | 3 |
| Полировка и проверка | 1 | 1 | 2 |
Максимум объёма работ в неделю составляет 360 чел-ч на изготовление частей стола, 240 чел-ч — на сборку и 180 чел-ч - на полировку. Рынок сбыта расширяется, но он недолговечен, а возможности хранения ограничивают производство 170 столами в неделю. Прибыль от продажи столов типов 1, 2, 3 составляет, соответственно, 15, 22 и 19 долл. Определите оптимальный план производства. Как изменится оптимальный план производства, если из-за беспорядков на участке изготовления частей стола объём работ в неделю сократился вдвое?
16. Объединение «Комфорт» производит холодильники, газовые плиты, морозильные шкафы и электропечи по цене 200, 180, 250 и 100 ден. ед., соответственно. Постоянным фактором, ограничивающим объёмы производства, является фиксированная величина трудовых ресурсов - 12000 человеко-часов в месяц. Выяснилось, однако, что в ближайший месяц дефицитной будет и листовая сталь для корпусов указанных изделий, поскольку поставщики смогут обеспечить лишь 7000 м2 этого материала.
Требуется составить план производства на данный месяц, с тем, чтобы максимизировать стоимость выпущенной продукции. Известно, что для изготовления холодильника требуется 2 м2 листовой стали и 3 чел-ч рабочего времени, для газовой плиты — соответственно 1,5 м2 и 3 чел-ч, для морозильного шкафа — 3 м2 и 4 чел-ч, для электропечи — 1 м2 и 2 чел-ч.
17. Участник экспедиции «Северный полюс» укладывает рюкзак, и ему требуется решить, какие положить продукты. В его распоряжении имеются мясо, мука, сухое молоко и сахар. В рюкзаке для продуктов осталось лишь 45 дм3 объёма, и нужно, чтобы суммарная масса продуктов не превосходила 35 кг. Врач экспедиции рекомендовал, чтобы мяса (по массе) было больше муки по крайней мере в два раза, муки не меньше молока, а молока по крайней мере в восемь раз больше, чем сахара. Сколько и каких продуктов нужно положить в рюкзак, с тем, чтобы суммарная калорийность продуктов была наибольшей? Характеристики продуктов приведены в таблице.
| Характеристики | Продукты | |||
| мясо | мука | молоко | сахар | |
| Объем (дм3/кг) | 1 | 1,5 | 2 | 1 |
| Калорийность (ккал/кг) | 1500 | 5000 | 5000 | 4000 |
18. На звероферме могут выращиваться песцы, чёрно-бурые лисы, нутрии и норки. Для их питания используются три вида кормов. В таблице приведены нормы расхода кормов, их ресурс в расчёте на день, а также прибыль от реализации одной шкурки каждого зверя.
| Вид корма | Норма расхода кормов (кг/день) | Ресурс кормов (кг) | |||
| песец | лиса | нутрия | норка | ||
| I | 1 | 2 | 1 | 2 | 300 |
| II | 1 | 4 | 2 | 0 | 400 |
| III | 1 | 1 | 3 | 2 | 600 |
| Прибыль д.е./шкурка | 6 | 12 | 8 | 10 | |
Определите, сколько и каких зверьков следует выращивать ферме, чтобы прибыль от реализации шкурок была наибольшей.
19. Завод изготавливает корпуса холодильников и комплектует их оборудованием, поставляемым без ограничений другими предприятиями. В таблице указаны нормы трудозатрат, затрат материалов для изготовления корпусов, ограничения по этим ресурсам в расчёте на месяц и прибыль от реализации холодильников каждой из пяти марок.
Найти месячный план выпуска холодильников, максимизирующий прибыль.
| Наименование ресурса | Марка холодильника | Объём ресурса | ||||
| 1 | 2 | 3 | 4 | 5 | ||
| Трудозатраты (чел-ч) | 2 | 3 | 5 | 4 | 4 | 9000 |
| Металл (м2) | 2 | 2 | 4 | 5 | 0 | 8500 |
| Пластик (м2 ) | 1 | 3 | 2 | 0 | 4 | 4000 |
| Краска (кг) | 1 | 2 | 3 | 3 | 2 | 5000 |
| Прибыль (ден. ед.) | 40 | 70 | 120 | 120 | 50 | |
20. Компания производит сверлильные станки трёх видов D1, D2, DЗ. Каждый вид приносит, соответственно 10, 10 и 30 долл. прибыли. Количество станков, которое может быть произведено в течение недели, ограничено поставками комплектующих изделий F1, F2, FЗ, где для D1 требуется 1 штука F1, 4 штуки F2 и 2 штуки FЗ, для D2 - 2штуки F1, 3 штуки F2 и 3 штуки FЗ, а для DЗ — 10 штук F1, 10 штук F2 и 8 штук FЗ. Каждую неделю количество доступных изделий F1, F2, FЗ составляет, соответственно, 650, 850 и 650 штук.
А. Определите максимальную прибыль, которую можно получать в неделю, какое количество станков D1, D2, D3 выгоднее всего производить?
Б. Компания обращается в комиссию по ценам за разрешением повысить цены до такой степени, чтобы они давали 20%-ное увеличение прибылей от всех моделей. Рассмотрев вопрос, комиссия разрешает увеличение цен на станки D1 и D2, но настаивает на таком ограничении цены на станок D3, при котором прибыль от продажи станка D3 уменьшилась бы на 10%. Стоит ли компании соглашаться с вариантом, предложенным комиссией по ценам? Что в этом случае произойдёт с прибылью?
21. Торговая фирма для продажи товаров трёх видов использует ресурсы: время и площадь торговых залов. Затраты ресурсов на продажу одной партии товаров каждого вида даны в таблице. Прибыль, получаемая от реализации одной партии товаров 1 вида – 5 у.е., 2 вида – 8 у.е., 3 вида – 6 у.е. Определить оптимальную структуру товарооборота, обеспечивающую фирме максимальную прибыль.
| Ресурсы | Вид товара | Объём ресурсов | ||
| 1 | 2 | 3 | ||
| Время, чел.-час | 0,5 | 0,7 | 0,6 | 370 |
| Площадь, м2 | 0,1 | 0,3 | 0,2 | 90 |
22. Для изготовления трёх видов A, B и C используется токарное, фрезерное, сварочное и шлифовальное оборудование. Затраты времени на обработку одного изделия для каждого из типов оборудования указаны в таблице. В ней же указан общий фонд рабочего времени каждого из типов используемого оборудования, а также прибыль от реализации изделия данного вида.
| Тип оборудования | Затраты времени (станко-ч) на обработку одного изделия данного вида | Общий фонд рабочего времени оборудования (ч) | ||
| A | B | C | ||
| Фрезерное | 2 | 4 | 5 | 120 |
| Токарное | 1 | 8 | 6 | 280 |
| Сварочное | 7 | 4 | 5 | 240 |
| Шлифовальное | 4 | 6 | 7 | 360 |
| Прибыль (руб.) | 10 | 14 | 12 | |
Требуется определить, сколько изделий и какого вида следует изготовить предприятию, чтобы прибыль от их реализации была максимальной.
23. Предприятие рекламирует свою продукцию с использованием четырёх источников массовой информации: телевидения, радио, газет и расклейки объявлений. Анализ рекламной деятельности в прошлом показал, что эти средства приводят к увеличению прибыли соответственно на 10, 5, 7 и 4 у. е., в расчёте на 1 у. е., затраченную на рекламу. На рекламу выделено 50000 у. е. Администрация предприятия не намерена тратить на телевидение более 40 %, на радио и газеты – более 50 % от общей суммы выделенных средств. Как следует предприятию организовать рекламу, чтобы получить максимальную прибыль?
24. Торговое предприятие планирует организовать продажу четырёх видов товара (А, В, С и Д), используя при этом только два вида ресурсов: рабочее время продавцов в количестве 840 ч и площадь торгового зала 180 м2. При этом известны плановые нормативы затрат этих ресурсов в расчёте на единицу товаров А, В, С и Д и прибыль от их продажи, которые приведены в таблице.
| Показатели | Товар | Общее количество ресурсов | |||
| А | В | С | Д | ||
| Расход рабочего времени на единицу товара (ч) | 0,6 | 0,8 | 0,6 | 0,4 | 840 |
| Использование площади торгового зала на единицу товара (м2) | 0,1 | 0,2 | 0,4 | 0,1 | 180 |
| Прибыль от продажи единицы товара (руб.) | 5 | 8 | 7 | 9 | |
25. Кондитерская фабрика для производства трёх видов карамели А, В и С использует три вида основного сырья: сахарный песок, патоку и фруктовое пюре. Нормы расхода сырья каждого вида на производство 1 т карамели данного вида приведены в таблице. В ней же указано общее количество сырья каждого вида, которое может быть использовано фабрикой, а также приведена прибыль от реализации 1 т карамели данного вида.
| ли | Нормы расхода сырья (т) на 1 т карамели | Общее количество сырья (т) | ||
| А | В | С | ||
| Сахарный песок | 0,8 | 0,5 | 0,6 | 800 |
| Патока | 0,4 | 0,4 | 0,3 | 600 |
| Фруктовое пюре | - | 0,1 | 0,1 | 120 |
| Прибыль от реализации 1 т продукции | 108 | 112 | 126 | |
Найти план производства карамели, обеспечивающий максимальную прибыль от её реализации.
26. На швейной фабрике для изготовления четырёх видов изделий может быть использована ткань трёх артикулов. Нормы расхода тканей всех артикулов на пошив одного изделия приведены в таблице. В ней же указаны имеющееся в распоряжении фабрики общее количество тканей каждого артикула и цена одного изделия данного вида. Определить, сколько изделий каждого вида должна произвести фабрика, чтобы стоимость изготовленной продукции была максимальной.
Артикул ткани | Норма расхода ткани (м) на одно изделие вида | Общее количество ресурсов | |||
| 1 | 2 | 3 | 4 | ||
| I | 1 | - | 2 | 1 | 180 |
| II | - | 1 | 3 | 2 | 210 |
| III | 4 | 2 | - | 4 | 800 |
| Цена одного изделия (руб.) | 9 | 6 | 4 | 7 | |
27. Для производства продукции трёх видов А, В и С используется три различных вида сырья. Каждый из видов сырья может быть использован в объёме, соответственно не большем, чем 180, 210 и 236 кг. Нормы затрат каждого из видов сырья на единицу продукции данного вида и цена единицы продукции каждого вида приведены в таблице.
| Вид сырья | Нормы затрат сырья (кг) на единицу продукции | ||
| Изделие А | Изделие В | Изделие С | |
| I | 4 | 2 | 1 |
| II | 3 | 1 | 3 |
| III | 1 | 2 | 5 |
| Цена единицы продукции (руб.) | 10 | 14 | 12 |
Требуется определить план выпуска продукции, обеспечивающий максимальный её выпуск в стоимостном выражении.
28. Решить симплекс-методом задачу линейного программирования:
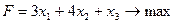
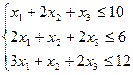
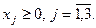
29. Решить симплекс-методом задачу линейного программирования:
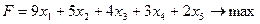
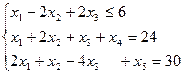
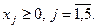
30. Найти решение задачи линейного программирования симплекс-методом:
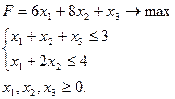
Транспортная задача
1. На 4 базы А1, А2, А3, А4 поступил однородный груз в количествах, соответственно равных 30, 25, 15 и 30 единиц. Этот груз требуется перевезти в 3 пункта назначения В1, В2, В3 соответственно в количествах 40, 20 и 40 единиц. Тарифы перевозок единицы груза с каждого из пунктов отправления в соответствующие пункты назначения указаны в транспортной таблице.
| Пункты отправления | Пункты назначения | Запасы | ||
| В1 | В2 | В3 | ||
| А1 | 3 | 5 | 4 | 30 |
| А2 | 4 | 2 | 1 | 25 |
| А3 | 1 | 3 | 2 | 15 |
| А4 | 5 | 3 | 5 | 30 |
| Потребности | 40 | 20 | 40 | 100 |
Опорный план перевозок найти методом северо-западного направления, оптимальный план перевозок - методом потенциалов.
2. Три предприятия данного экономического района могут производить некоторую однородную продукцию в количествах, соответственно равных 180, 350 и 20 единиц. Эта продукция должна быть поставлена пяти потребителям в количествах, соответственно равных 110, 90, 120, 80 и 150 ед. Затраты, связанные с производством и доставкой единицы продукции, задаются матрицей:
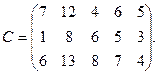
Составить такой план прикрепления потребителей к поставщикам, при котором общие затраты являются минимальными. Опорный план найти методом минимального элемента, оптимальный план – методом потенциалов.
3. При срочных поставках медикаментов критерием является минимальное время их доставки. Запасы вакцины и потребность в ней указаны в приведённой ниже таблице (в центнерах). Время доставки указано в часах. Найти оптимальный план поставок методом потенциалов. Опорный план найти методом минимального элемента.
| Ai/Bj | В1 | В2 | В3 | В4 | ai |
| А1 | 5 | 10 | 5 | 10 | 16 |
| А2 | 8 | 4 | 4 | 8 | 40 |
| А3 | 6 | 3 | 6 | 3 | 32 |
| А4 | 4 | 7 | 7 | 5 | 12 |
| bj | 30 | 10 | 20 | 40 | 100 |
4. На 4 базы А1, А2, А3, А4 поступил однородный груз в количествах, соответственно равных 30, 25, 15 и 30 единиц. Этот груз требуется перевезти в 3 пункта назначения В1, В2, В3 соответственно в количествах 40, 20 и 40 единиц. Тарифы перевозок единицы груза с каждого из пунктов отправления в соответствующие пункты назначения указаны в транспортной таблице.
| Пункты отправления | Пункты назначения | Запасы | ||
| В1 | В2 | В3 | ||
| А1 | 6 | 2 | 4 | 30 |
| А2 | 2 | 1 | 5 | 25 |
| А3 | 5 | 6 | 3 | 15 |
| А4 | 1 | 3 | 2 | 30 |
| Потребности | 40 | 20 | 40 | 100 |
Опорный план перевозок найти методом северо-западного направления, оптимальный план перевозок - методом потенциалов.
5. При размещении аптек в качестве критерия может быть принято расстояние от аптек до населенных пунктов. В приведённой ниже таблице указаны запасы антибиотиков, заявки (тыс. упаковок) и расстояния (в километрах). Найти оптимальный план размещения аптек методом потенциалов. Опорный план найти методом минимального элемента.
| Ai/Bj | В1 | В2 | В3 | В4 | В5 | В6 | ai |
| А1 | 2 | 1 | 2 | 4 | 3 | 5 | 120 |
| А2 | 5 | 4 | 2 | 8 | 6 | 7 | 60 |
| А3 | 1 | 2 | 3 | 2 | 1 | 3 | 80 |
| bj | 30 | 10 | 50 | 70 | 30 | 70 | 260 |
6. Для строительства четырёх объектов используется кирпич, изготовляемый на трёх заводах. Ежедневно каждый из заводов может изготовлять 100, 150 и 50 усл. ед. кирпича. Ежедневные потребности в кирпиче на каждом из строящихся объектов соответственно равны 75, 80, 60 и 85 усл. ед. Известны также тарифы перевозок 1 усл. ед. кирпича с каждого из заводов к каждому из строящихся объектов:
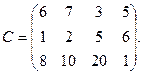
С помощью метода потенциалов составить такой план перевозок кирпича
к строящимся объектам, при котором общая стоимость перевозок является минимальной. Опорный план найти методом северо-западного направления.
7. На 4 базы А1, А2, А3, А4 поступил однородный груз в количествах, соответственно равных 30, 25, 15 и 30 единиц. Этот груз требуется перевезти
в 3 пункта назначения В1, В2, В3 соответственно в количествах 40, 20 и 40 единиц. Тарифы перевозок единицы груза с каждого из пунктов отправления
в соответствующие пункты назначения указаны в транспортной таблице.
| Пункты отправления | Пункты назначения | Запасы | ||
| В1 | В2 | В3 | ||
| А1 | 2 | 6 | 4 | 30 |
| А2 | 4 | 3 | 5 | 25 |
| А3 | 3 | 1 | 5 | 15 |
| А4 | 5 | 2 | 5 | 30 |
| Потребности | 40 | 20 | 40 | 100 |
Опорный план перевозок найти методом северо-западного направления, оптимальный план перевозок - методом потенциалов.
8. Фирма «Союз» обеспечивает доставку видео- и аудиокассет с четырёх складов, расположенных в разных точках города, в четыре магазина. Запас кассет, имеющихся на складах, а также объёмы заказов магазинов и тарифы на доставку представлены в транспортной таблице.
|
Склады | магазин | Запасы, тыс. шт. | |||
| №1 | №2 | №3 | №4 | ||
| Склад№1 | 2 | 6 | 4 | 3 | 120 |
| Склад№2 | 5 | 1 | 9 | 2 | 240 |
| Склад№3 | 3 | 2 | 2 | 6 | 80 |
| Склад№4 | 4 | 5 | 10 | 3 | 60 |
| Заказы, шт. | 190 | 170 | 110 | 30 | 500 |
Определите методом потенциалов объёмы перевозок, обеспечивающие их минимальные затраты. Опорный план найдите методом минимального элемента.
9. Используя метод минимального элемента, составить опорный план для перевозки фармацевтического сырья некоторого вида с четырёх оптовых складов на пять перерабатывающих фабрик. Запасы {ai} оптовых складов по поставке сырья (в тоннах), а также потребности {bj} и стоимости транспортировок тонны сырья с i-го оптового склада на j-ую фармацевтическую фабрику (где 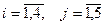 ) приведены в таблице.
) приведены в таблице.
Используя метод потенциалов, составить оптимальный план таких перевозок и найти его минимальную стоимость.
| Ai | Вj | ai | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | 17 | 20 | 29 | 26 | 25 | 15 |
| А2 | 3 | 4 | 5 | 15 | 24 | 15 |
| А3 | 19 | 2 | 22 | 4 | 13 | 15 |
| A4 | 20 | 27 | 1 | 17 | 19 | 15 |
| bj | 11 | 11 | 11 | 11 | 16 | 60 |
10. На 4 базы А1, А2, А3, А4 поступил однородный груз в количествах, соответственно равных 30, 25, 15 и 30 единиц. Этот груз требуется перевезти в 3 пункта назначения В1, В2, В3 соответственно в количествах 40, 20 и 40 единиц. Тарифы перевозок единицы груза с каждого из пунктов отправления в соответствующие пункты назначения указаны в транспортной таблице.
| Пункты отправления | Пункты назначения | Запасы | ||
| В1 | В2 | В3 | ||
| А1 | 5 | 4 | 3 | 30 |
| А2 | 2 | 3 | 3 | 25 |
| А3 | 3 | 1 | 2 | 15 |
| А4 | 1 | 2 | 5 | 30 |
| Потребности | 40 | 20 | 40 | 100 |
Опорный план перевозок найти методом северо-западного направления, оптимальный план перевозок - методом потенциалов.
11. Московский филиал фирмы «The Coca-Cola Companу», выпускающей газированные напитки приблизительно равного спроса (Sprite, Coca-Cola, Fanta), складируемые в разных местах, должен поставить свою продукцию в четыре крупных московских супермаркета: «Рамстор–1», «Рамстор–2», «Седьмой континент», «Арбатский». Каждая упаковка содержит 12 банок ёмкостью 0,33 литра. Тарифы на доставку товара, объёмы запасов и заказы на продукцию приведены в таблице.
|
Склады | Супермаркеты | Запасы, тыс. шт. | |||
| «Рамстор–1» | «Рамстор–2» | «Седьмой континент» | «Арбатский» | ||
| Coca-Cola | 6 | 4 | 9 | 5 | 400 |
| Sprite | 5 | 7 | 8 | 6 | 300 |
| Fanta | 9 | 4 | 6 | 7 | 200 |
| Заказы, уп. | 150 | 250 | 150 | 350 | 900 |
Определите методом потенциалов оптимальный план поставок газированных напитков в супермаркеты города и затраты на перевозку. Опорный план найдите методом минимального элемента.
12. На трёх хлебокомбинатах производится 110, 190 и 90 т муки. Эта мука потребляется хлебозаводами, ежедневные потребности которых равны соответственно 80, 60, 170 и 80 т. Тарифы перевозок 1 т муки с хлебокомбинатов к каждому из хлебозаводов задаются матрицей:
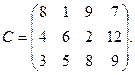
Составить с помощью метода потенциалов такой план доставки муки, при котором общая стоимость перевозок является минимальной. Опорный план найти методом минимального элемента.
13. На 4 базы А1, А2, А3, А4 поступил однородный груз в количествах, соответственно равных 30, 25, 15 и 30 единиц. Этот груз требуется перевезти в 3 пункта назначения В1, В2, В3 соответственно в количествах 40, 20 и 40 единиц. Тарифы перевозок единицы груза с каждого из пунктов отправления в соответствующие пункты назначения указаны в транспортной таблице.
| Пункты отправления | Пункты назначения | Запасы | ||
| В1 | В2 | В3 | ||
| А1 | 5 | 3 | 4 | 30 |
| А2 | 2 | 6 | 5 | 25 |
| А3 | 4 | 4 | 3 | 15 |
| А4 | 5 | 3 | 2 | 30 |
| Потребности | 40 | 20 | 40 | 100 |
Опорный план перевозок найти методом северо-западного направления, оптимальный план перевозок методом - потенциалов.
14. Четыре предприятия данного экономического района для производства продукции используют некоторое сырьё. Спрос на сырьё каждого из предприятий соответственно составляет: 120, 50, 190 и 110 усл. ед. Сырьё сосредоточено в трёх местах. Предложения поставщиков сырья равны: 160, 140 и 170 усл. ед. На каждое предприятие сырьё может завозиться от любого поставщика. Тарифы перевозок известны и задаются матрицей:
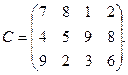
В i-ой строке и j-ом столбце матрицы С стоит тариф на перевозку сырья от i-го поставщика к j-ому потребителю, 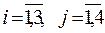 . Под тарифом понимается стоимость перевозки единицы сырья. Требуется составить с помощью метода потенциалов план перевозок, при котором общая стоимость перевозок минимальна. Опорный план найти методом минимального элемента.
. Под тарифом понимается стоимость перевозки единицы сырья. Требуется составить с помощью метода потенциалов план перевозок, при котором общая стоимость перевозок минимальна. Опорный план найти методом минимального элемента.
15. Используя метод минимального элемента, составить опорный план для перевозки фармацевтического сырья некоторого вида с четырёх оптовых складов на пять перерабатывающих фабрик. Запасы {ai} оптовых складов по поставке сырья (в тоннах), а также потребности {bj} стоимости транспортировок тонны сырья с i-го оптового склада на j-ую фармацевтическую фабрику (где 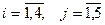 ) приведены в таблице.
) приведены в таблице.
Используя метод потенциалов, составить оптимальный план таких перевозок и найти его минимальную стоимость.
| Ai | Вj | ai | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | 3 | 25 | 11 | 22 | 12 | 23 |
| А2 | 9 | 15 | 4 | 26 | 12 | 25 |
| А3 | 13 | 22 | 15 | 12 | 27 | 12 |
| A4 | 6 | 19 | 8 | 11 | 8 | 30 |
| bj | 18 | 18 | 18 | 18 | 18 | 90 |
16. На 4 базы А1, А2, А3, А4 поступил однородный груз в количествах, соответственно равных 30, 25, 15 и 30 единиц. Этот груз требуется перевезти в 3 пункта назначения В1, В2, В3 соответственно в количествах 40, 20 и 40 единиц. Тарифы перевозок единицы груза с каждого из пунктов отправления в соответствующие пункты назначения указаны в транспортной таблице.
| Пункты отправления | Пункты назначения | Запасы | ||
| В1 | В2 | В3 | ||
| А1 | 5 | 3 | 1 | 30 |
| А2 | 3 | 4 | 5 | 25 |
| А3 | 4 | 2 | 3 | 15 |
| А4 | 2 | 4 | 5 | 30 |
| Потребности | 40 | 20 | 40 | 100 |
Опорный план перевозок найти методом северо-западного направления, оптимальный план перевозок - методом потенциалов.
17. Фирма «Московия» заключила контракт с компанией АЛРОСА (алмазы «России -Саха») на покупку промышленного золота для его реализации в пяти городах в объёмах: Самара – 80 кг, Москва – 260 кг, Ростов–на-Дону – 100 кг, Санкт-Петербург – 140 кг, Нижний Новгород – 120 кг.
Компания располагает тремя месторождениями «Мирное», «Удачное»
и «Полевое», которые планируют за год выработать соответственно 200, 250
и 250 кг золота. Определите методом методом потенциалов (опорный план найдите методом минимального элемента) стоимость фрахта специализированного транспорта, обеспечивающую полное удовлетворение заявок покупателей, при заданной матрице тарифов:
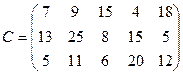 .
.
18. На 4 базы А1, А2, А3, А4 поступил однородный груз в количествах, соответственно равных 30, 25, 15 и 30 единиц. Этот груз требуется перевезти
в 3 пункта назначения В1, В2, В3 соответственно в количествах 40, 20 и 40 единиц. Тарифы перевозок единицы груза с каждого из пунктов отправления
в соответствующие пункты назначения указаны в транспортной таблице.
| Пункты отправления | Пункты назначения | Запасы | ||
| В1 | В2 | В3 | ||
| А1 | 2 | 5 | 4 | 30 |
| А2 | 1 | 4 | 5 | 25 |
| А3 | 2 | 6 | 5 | 15 |
| А4 | 4 | 3 | 1 | 30 |
| Потребности | 40 | 20 | 40 | 100 |
Опорный план перевозок найти методом северо-западного направления, оптимальный план перевозок - методом потенциалов.
19. На 4 базы А1, А2, А3, А4 поступил однородный груз в количествах, соответственно равных 30, 25, 15 и 30 единиц. Этот груз требуется перевезти
в 3 пункта назначения В1, В2, В3 соответственно в количествах 40, 20 и 40 единиц. Тарифы перевозок единицы груза с каждого из пунктов отправления
в соответствующие пункты назначения указаны в транспортной таблице.
| Пункты отправления | Пункты назначения | Запасы | ||
| В1 | В2 | В3 | ||
| А1 | 3 | 1 | 3 | 30 |
| А2 | 5 | 4 | 2 | 25 |
| А3 | 4 | 3 | 5 | 15 |
| А4 | 1 | 5 | 5 | 30 |
| Потребности | 40 | 20 | 40 | 100 |
Опорный план перевозок найти методом северо-западного направления, оптимальный план перевозок - методом потенциалов.
20. Составьте методом потенциалов оптимальный план завоза хлебобулочной продукции с минимальными транспортными затратами из трёх пекарен фирмы «Колос» в четыре булочных города: А, B, C, D. Заказы
на поставку хлебобулочных изделий, производительность пекарен
и транспортные тарифы представлены в таблице. Опорный план найдите методом минимального элемента.
| Мини-пекарни | Булочные | Производительность пекарен, кг/сутки | |||
| A | B | C | D | ||
| №1 | 4 | 7 | 6 | 10 | 830 |
| №2 | 9 | 6 | 7 | 5 | 670 |
| №3 | 6 | 7 | 5 | 8 | 770 |
| Заказы, кг/сутки | 520 | 610 | 380 | 760 | 2270 |
21. Фирма по прокату автомобилей «Золотое кольцо России» собирает заявки на аренду во всех городах центра России. Клиент имеет возможность получить автомобиль в любом удобном для него населенном пункте и оставить его в любом месте, где он заканчивает путешествие, в том числе и в своём родном городе. Работники фирмы забирают оставленные автомобили и перегоняют их для передачи новым клиентам. Сейчас 4 автомобиля компании оставлены в Клину, 3 - в Ростове Великом, 6 - в Ярославле и 1 - в Серпухове. Имеются заказы на 5 автомобилей во Владимире, на 3 автомобиля в Санкт-Петербурге и на 6 автомобилей в Москве.
Расстояния между городами (в км) приведены в следующей таблице:
| Города | Владимир | Санкт-Петербург | Москва |
| Клин | 300 | 550 | 100 |
| Ростов Великий | 200 | 620 | 200 |
| Ярославль | 350 | 570 | 250 |
| Серпухов | 250 | 700 | 150 |
Составьте с помощью метода потенциалов план, по которому следует перегонять автомобили новым клиентам. Ориентируйтесь на минимизацию расстояния, которое пройдут все перегоняемые автомобили. Опорный план перевозок найдите методом минимального элемента.
22. На 4 базы А1, А2, А3, А4 поступил однородный груз в количествах, соответственно равных 30, 25, 15 и 30 единиц. Этот груз требуется перевезти
в 3 пункта назначения В1, В2, В3 соответственно в количествах 40, 20 и 40 единиц. Тарифы перевозок единицы груза с каждого из пунктов отправления
в соответствующие пункты назначения указаны в транспортной таблице.
| Пункты отправления | Пункты назначения | Запасы | ||
| В1 | В2 | В3 | ||
| А1 | 2 | 4 | 3 | 30 |
| А2 | 2 | 5 | 2 | 25 |
| А3 | 4 | 1 | 4 | 15 |
| А4 | 5 | 3 | 5 | 30 |
| Потребности | 40 | 20 | 40 | 100 |
Опорный план перевозок найти методом северо-западного направления, оптимальный план перевозок - методом потенциалов.
23. В таблице приведены расходы по перевозке товаров с четырёх фабрик на 3 склада, расположенные в различных местах. Расходы даны в $ на единицу товара.
| Фабрики | Склады | ||
| X | Y | Z | |
| А | 15 | 40 | 25 |
| Б | 10 | 35 | 15 |
| В | 45 | 20 | 9 |
| Г | 30 | 35 | 15 |
Месячный объём выпуска фабрик следующий: А: 8 единиц; Б: 17 единиц; В: 11 единиц; Г: 10 единиц. Месячная потребность складов следующая: Х: 11 единиц; У: 13 единиц; Z: 22 единицы.
С помощью метода потенциалов найдите оптимальную стратегию перевозки товаров от фабрик к складам, которая позволит минимизировать общие затраты. Опорный план найдите методом северо-западного направления.
24. Электронная компания имеет четыре центра сбыта и четыре крупных розничных магазина, расположенных в Калифорнии. Расстояния между центрами и магазинами указаны в таблице. Также указано количество партий компьютерных систем, имеющихся в наличии в каждом из центров сбыта, и потребность в них в каждом из магазинов:
| Центры сбыта | Розничные магазины | Всего в наличии | |||
| А | Б | В | Г | ||
| 1 | 90 | 350 | 300 | 40 | 8 |
| 2 | 60 | 130 | 200 | 300 | 4 |
| 3 | 450 | 300 | 350 | 110 | 18 |
| 4 | 300 | 450 | 500 | 250 | 10 |
| Потребность | 6 | 7 | 10 | 17 | 40 |
С помощью метода потенциалов предложите маршруты перевозки партий с помощью компьютерных систем, которые минимизируют общий километраж. Опорный план найдите методом минимального элемента.
25. На 4 базы А1, А2, А3, А4 поступил однородный груз в количествах, соответственно равных 30, 25, 15 и 30 единиц. Этот груз требуется перевезти
в 3 пункта назначения В1, В2, В3 соответственно в количествах 40, 20 и 40 единиц. Тарифы перевозок единицы груза с каждого из пунктов отправления
в соответствующие пункты назначения указаны в транспортной таблице.
| Пункты отправления | Пункты назначения | Запасы | ||
| В1 | В2 | В3 | ||
| А1 | 3 | 1 | 4 | 30 |
| А2 | 6 | 3 | 2 | 25 |
| А3 | 6 | 5 | 3 | 15 |
| А4 | 2 | 3 | 5 | 30 |
| Потребности | 40 | 20 | 40 | 100 |
Опорный план перевозок найти методом северо-западного направления, оптимальный план перевозок - методом потенциалов.
26. Определить с помощью метода потенциалов транспортные связи между пунктами производства и потребления, обеспечивающие поставки лесоматериалов с минимальными общими затратами на производство и поставку. Исходные данные указаны в таблице. Опорный план найти методом минимального элемента.
Пункты и объёмы производства | Пункты и объёмы потребления | ||||
| В1 | В2 | В3 | В4 | ||
| 180 | 200 | 150 | 120 | ||
| Затраты на производство и поставку 1м3, руб. | |||||
| А1 | 190 | 5 | 4 | 3 | 2 |
| А2 | 200 | 4 | 7 | 4 | 4 |
| А3 | 160 | 3 | 5 | 6 | 8 |
| А4 | 100 | 4 | 3 | 7 | 5 |
27. В трёх аптечных управлениях скопился излишек ai (тыс. упаковок) витамина C. В пяти других аптечных управлениях его недостаток составил bj (тыс. упаковок). Стоимости перевозки 1 тыс. упаковок (в десятках руб.) указаны в таблице. Найти оптимальный план перевозок методом потенциалов. Опорный план найти методом минимального элемента.
| Ai/Bj | B1 | B2 | B3 | B4 | B5 | ai |
| A1 | 8 | 6 | 10 | 4 | 7 | 11 |
| A2 | 9 | 5 | 9 | 6 | 3 | 14 |
| A3 | 7 | 5 | 8 | 5 | 4 | 15 |
| bj | 5 | 7 | 6 | 13 | 9 | 40 |
28. При срочных поставках медикаментов критерием является минимальное время их доставки. Запасы вакцины и потребность в ней указаны в таблице (в центнерах). Время доставки указано в часах. Найти оптимальный план поставок методом потенциалов. Опорный план найти методом минимального элемента.
| Ai/Bj | B1 | B2 | B3 | B4 | ai |
| A1 | 5 | 10 | 5 | 10 | 16 |
| A2 | 8 | 4 | 4 | 8 | 40 |
| A3 | 6 | 3 | 6 | 3 | 32 |
| A4 | 4 | 7 | 7 | 5 | 12 |
| bj | 30 | 10 | 20 | 40 | 100 |
29. Решить транспортную задачу, заданную распределительной таблицей:
| Ai/Bj | B1 | B2 | B3 | B4 | ai |
| A1 | 6 | 8 | 15 | 4 | 60 |
| A2 | 9 | 15 | 2 | 3 | 130 |
| A3 | 6 | 12 | 7 | 1 | 90 |
| bj | 30 | 80 | 60 | 110 | 280 |
Найти оптимальный план методом потенциалов. Опорный план найти методом минимального элемента.
30. Решить транспортную задачу, заданную распределительной таблицей:
| Ai/Bj | B1 | B2 | B3 | B4 | ai |
| A1 | 1 | 3 | 4 | 5 | 90 |
| A2 | 5 | 3 | 1 | 2 | 30 |
| A3 | 2 | 1 | 4 | 2 | 40 |
| bj | 70 | 30 | 20 | 40 | 160 |
Найти оптимальный план методом потенциалов. Опорный план найти методом минимального элемента.








