РИС. 1. Простейшая структура тенсегрити в виде треноги (3-призма).
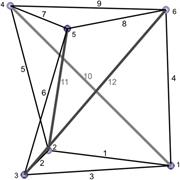
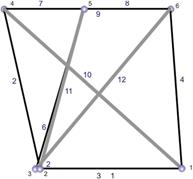
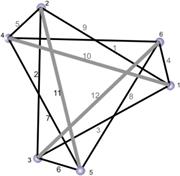
 a) b) c)
a) b) c)
ZXY 
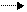
РИС. 2. Устойчивая форма 3-призмы (треноги тенсегрити): a ) Общий вид, b ) Вид сбоку, c ) Вид сверху.
TАБЛИЦА 2. Рассчитанные (точные) и измеренные собственные частоты треноги
w id. (rad/s)
w exact Sensors (locations)
Mode
(rad/s)
9 8 7 6 5 4 3
(1 2 3 4 5 6 7 8) (1 2 3 4 5 6 7) (1 2 3 4 5 6) (1 2 3 4 5) (1 3 5 8) (3 4 7)
1 6.723 6.688 6.575 6.7103 6.733 6.852 6.711 6.553
2 57.194 57.060 56.999 56.164 55.791 55.932 56.564 57.546
3 57.197 57.673 57.192 56.917 57.112 57.123 57.577
4 131.217 130.685 129.835 129.685 129.491 129.002 127.848 127.371
5 131.219 131.261 131.908 131.234 133.289 130.124 132.725 129.469
6 156.611 156.800 156.242 156.294 157.106 156.027 157.506 151.489
7 755.773 756.168 750.265 744.163 755.309 750.766
8 755.790 756.260 755.077 755.262 756.324 755.016 762.064 755.910
9 766.354 766.832 767.444 763.797 763.518 764.262 766.525 765.711
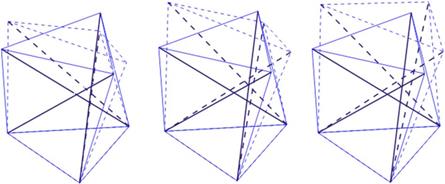
(см. рис. 3б) наблюдается поворот верхних треугольных тросов относительно оси, параллельной направлению седьмого троса и пересекающей середины пролетов восьмого и девятого тросов.
Для третьей моды (рис. 3в) получаются такие же деформации, как и для второй, происходящей почти с той же собственной частотой, т. е. вращение верхних треугольных тросов относительно оси, параллельной направлению восьмого троса и пересекающей середины пролетов седьмого и девятого тросов.
Четвёртая мода (рис. 3г) характеризуется деформацией верхних треугольных тросов таким образом, что при растяжении восьмого троса укорачиваются тросы № 7 и 9 и, наоборот, при удлинении седьмого и девятого тросов трос число 8 укорочено. Эти деформации сопровождаются попеременными поворотами верхних треугольных тросов относительно осей вращения, характеризующих второй и третий режимы.
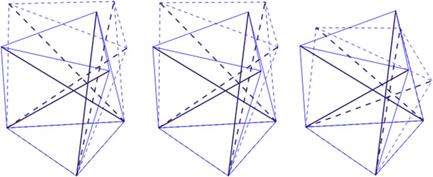
Для пятой моды получаются такие же деформации (рис. 3д), как и для четвертой, которая происходит почти с той же собственной частотой, поэтому пятая мода характеризуется деформацией верхних треугольных тросов таким образом, что при девятом тросе натянуты, тросы № 7 и 8 укорочены и наоборот, когда седьмой и восьмой тросы удлинены, трос № 9 укорочен, и наблюдаются те же повороты.
Для шестой моды (рис. 3е) верхние треугольные тросы укорачиваются (усаживаются) при вертикальном растяжении симплекса по оси Z и удлиняются (расширяются) при вертикальном укорочении симплекса.
Для моды 7 (рис. 3г) наблюдается поворот верхних треугольных тросов относительно оси, параллельной направлению седьмого троса и пересекающей середины пролетов восьмого и девятого тросов. За этим поворотом следует деформация верхних треугольных тросов таким образом, что при растяжении седьмого троса укорачиваются тросы № 8 и 9 и, наоборот, при удлинении восьмого и девятого тросов укорачивается трос № 7.
Для восьмой моды получаются такие же деформации (рис. 3ж), как и для седьмой, имеющей почти ту же собственную частоту, при этом наблюдается поворот
a) b) c)
d) e) f)
g) h) i)
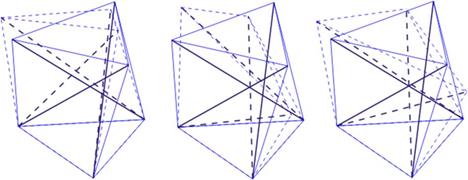
РИС. 3. Девять модовых форм 3-призмы (треноги)
верхних треугольных тросов относительно оси, параллельной направлению девятого троса и пересекающих средние пролеты седьмого и восьмого тросов. За этим вращением следует деформация верхних треугольных тросов таким образом, что при растяжении девятого троса укорачиваются тросы № 7 и 8 и, наоборот, при удлинении седьмого и восьмого тросов укорачивается трос № 9.
В девятом моде (рис. 3з) верхние треугольные тросы удлиняются (расширяются) при вертикальном растяжении симплекса по оси Z и укорачиваются (сжимаются) при вертикальном укорочении треноги.
Структура возбуждается случайными силами. Всего было создано 30000 точек данных с частотой дискретизации 4000 Гц. К выходным сигналам добавляется 2% шума для имитации шума измерения.
Существует несколько реализаций метода стохастических подпространств; одним из которых является алгоритм сбалансированной реализации (BR). Этот метод основан на SVD-разложении матрицы Ганкеля Hp+1,q, связанной с системой состояний уравнения (8).
Practical experience with real data as investigated by (Reynders et al. 2007) showed that it is better to over specify the model order and to eliminate spurious numerical poles aferwards. Tis can be done by constructing stabilization diagrams. By rejecting less singular values, models of increasing order are determined. Each model yields a set of modal parameters and these can be plotted in a stabilization diagram. The criteria used are 1% for eigenfrequencies, 5% for damping ratios and 99% for mode shape vectors (MAC). A mode (frequency, damping and modal shape) is considered stable if it satisfes these three criteria.
Практический опыт работы с реальными данными (Рейндерс и др., 2007 г.) показал, что лучше указать порядок модели и исключить ложные числовые выбросы в дальнейшем. Это можно сделать, построив схемы стабилизации. Путем отбрасывания менее сингулярных значений определяются модели возрастающего порядка. Каждая модель даёт набор модальных параметров, которые можно изобразить на диаграмме стабилизации. Используемые критерии: 1% для собственных частот, 5% для коэффициентов демпфирования и 99% для векторов формы моды (MAC). Мода (частота, затухание и модальная форма) считается устойчивой, если она удовлетворяет этим трём критериям.
Пробная схема стабилизации реализована в виде мульти-патч со всеми датчиками. Поскольку используются все возможные датчики, можно строить разные анимированные формы режима.
Были изучены данные при различных местоположениях датчиков, чтобы определить девять форм колебаний треноги и соответствующие им собственные частоты и коэффициенты демпфирования. В таблице 2 приведены значения точных и идентифицированных собственных частот для каждого из датчиков. В таблице 3 приведены значения точного и идентифицированного коэффициента демпфирования для различных наборов датчиков. Сравнение этих двух таблиц показывает, что идентифицированные собственные частоты и коэффициенты затухания для большинства наборов датчиков были хорошо идентифицированы. Однако в случае, когда использовались шесть датчиков, расположенных по степеням свободы 1, 2, 3, 4, 5 и 6, и в случае, когда использовались пять датчиков, расположенных по степеням свободы 1, 2, 3, 4 и 5, седьмой режим был не идентифицирован. Следует отметить, что седьмая мода возникает почти на той же частоте, что и мода 8, и имеет симметричную форму деформации. Это же наблюдалось и для случая, когда использовались три датчика, расположенные по степеням свободы 3, 4 и 7 - третья мода не идентифицировалась. Эта мода возникает почти на той же частоте, что и мода 2, и имеет симметричную форму деформации. Это может быть связано с определенными условиями, которые, как известно, зависят от местоположения датчика (этот вопрос не рассматривается в этой статье) и с постоянством возбуждения. Поскольку эти близкие моды трудно разделить только по частотам, мы ввели в этой работе использование значения MAC на диаграмме стабилизации, чтобы разделить моды. MAC между точной и идентифицированной формами колебаний структуры 3-призмы представлены в таблице 4. Проверка
TАБЛИЦА 3. Точные и идентифицированные коэффициенты демпфирования конструкции 3-призмы (треноги).
V id. (%)
V exact Sensors (locations)
Mode
(%)
9 8 7 6 5 4 3
(1 2 3 4 5 6 7 8) (1 2 3 4 5 6 7) (1 2 3 4 5 6) (1 2 3 4 5) (1 3 5 8) (3 4 7)
1 5.00 5,12 5,78 4,93 4,39 4,86 3,06 4,79
2 5.00 4,87 5,12 4,43 3,50 5,45 6,87 4,77
3 5.00 5,12 4,26 4,85 5,85 3,15 4,39
4 5.00 5,16 5,51 5,89 7,44 4,91 7,47 4,59
5 5.00 7,58 4,76 4,95 3,82 7,70 5,69 6,32
6 5.00 5,64 4,84 5,64 6,96 5,77 5,75 4,85
7 5.00 4,86 5,23 6,20 4,86 5,74
8 5.00 4,67 4,70 5,01 5,29 5,10 5,37 5,07
9 5.00 5,83 5,26 5,11 5,01 5,48 5,28 5,41
TАБЛИЦА 4. MAC между точной и идентифицированной формой колебаний 3-призмы (треноги).
Mac (identifed mode – exact mode)
w exact Sensors (locations)
Mode
(rad/s) 9 8 7 6 5 4 3
(1 2 3 4 5 6 7 8) (1 2 3 4 5 6 7) (1 2 3 4 5 6) (1 2 3 4 5) (1 3 5 8) (3 4 7)
1 6.723 99.99 99.99 99.99 99.99 99.99 99.99 99.99
2 57.194 97.86 89.80 85.01 97.09 94.17 95.73 99.58
3 57.197 99.69 95.10 92.55 98.24 98.81 85.90
4 131.217 97.23 91.64 97.26 98.76 95.42 98.20 98.77
5 131.219 97.09 97.60 92.55 92.46 81.77 85.94 85.90
6 156.611 99.87 99.84 99.95 99.28 99.87 98.99 84.73
7 755.773 90.04 98.34 97.04 94.26 94.52
8 755.790 93.91 96.73 98.60 95.01 98.54 86.49 85.67
9 766.354 99.22 96.79 96.17 99.30 98.23 99.46 88.89
Эта таблица показывает, что в целом формы мод были хорошо идентифицированы, за исключением близких мод и в зависимости от расположения датчиков. Однако для коэффициентов демпфирования идентифицированные значения были менее точными, чем для частот. Это наблюдение присуще алгоритмам стохастической идентификации, о которых сообщалось в литературе (Magalhães et al. 2009).
Для проверки идентификации параметров формы были рассчитаны корреляции данных на основе модели и сопоставлены с эмпирическими (или, что эквивалентно, соответствующие спектры). Датчики 3, 4 и 7 использовались для определения экспериментальных собственных частот, коэффициентов затухания, форм колебаний и корреляций из первых 30000 выборок данных. Наложенные корреляции показаны на рис. 4. Рассмотрение этого рисунка показывает, что модальная модель хорошо воспроизводит эмпирические корреляции, и это может быть связано с тем фактом, что большинство мод были хорошо определены.
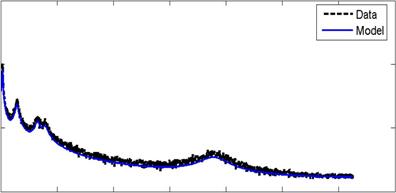
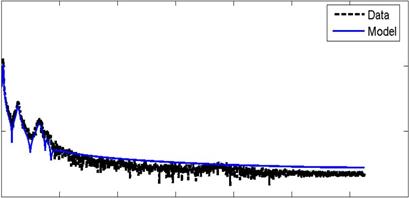
Вторым методом подтверждения идентификации системы является спектральный анализ. На рис. 5 представлены древовидные спектры, которые сравниваются со спектрами, полученными путём применения БПФ к результатам измерений. Из этих сравнений спектров модели и данных видно, что параметры структурной модели в целом хорошо идентифицируются, несмотря на расхождение в автоспектре датчика 3. На самом деле, пики на рис.5а, б, в лучше определяются, чем провалы, что можно понять из реализации метода Cov-SSI, который не гарантирует условие положительной реальной последовательности (Van Overchee, De Moor, 1996). Следовательно, расширенные ковариационные матрицы могут не быть положительными, таким образом, расходимости спектра вполне оправданы.
a) –10
x10 Correlation between output 3 and output 3
1.5
Model based
1 Empirical
0.5
0
–0.5
–1
–1.5
0 500 1000 1500 2000 2500
Time Log index
b) –10
x10 Correlation between output 3 and output 4
4
Model based
Empirical
2
0
-2
-4
-6
0 500 1000 1500 2000 2500
Time Log index
c)
–10
x10 Correlation between output 3 and output 7
3
Model based
Empirical
2
1
0
–1
–2
0 500 1000 1500 2000 2500
Time Log index
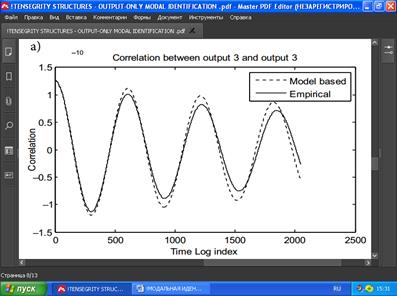
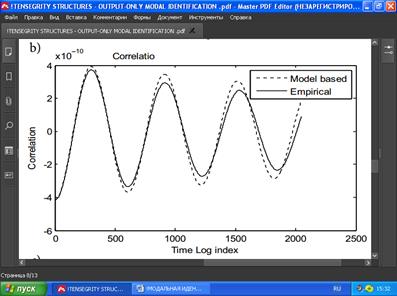
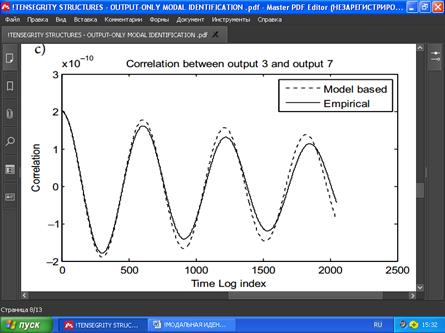
РИС. 4. Эмпирические корреляции в сравнении с модельными корреляциями для 3-призмы.
a)
b)
c)
10–10
10–15
–20
10 0 200 400 600 800 1000 1200 1400
Frequencies (Hz)
c)
FFT vs Model spectrum
10–5
Data
Model
–10
10
10–15
10–20
0 200 400 600 800 1000 1200 1400
Frequencies (Hz)
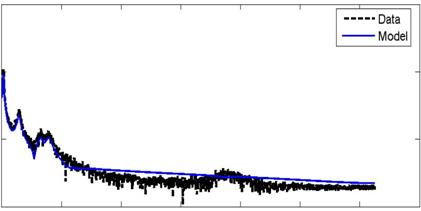
РИС. 5. Взаимный спектр 3-призмы: (а) Автоспектр с датчика 3, (б) Взаимный спектр между данными с датчиков 3 и 4, (в) Взаимный спектр с датчиков 3 и 7.
a)
FFT vs Model spectrum
10–5
Data
Model
10–10
10–15
10–20
0 200 400 600 800 1000 1200 1400
Frequencies (Hz)
b)
FFT vs Model spectrum
10–5
Data
Model
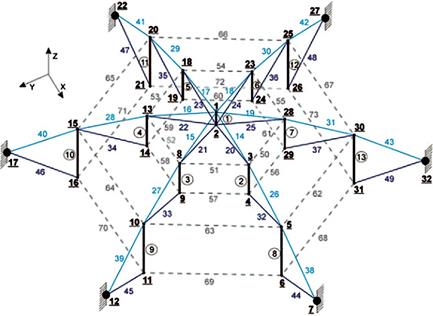
Fig. 6. Дом тенсегрити в виде купола Гейгера.
3.2. КУПОЛ ГЕЙГЕРА
Вторым рассмотрен сложный пример — мелкомасштабный купол тенсегрити гейгеровского типа. Модель структуры типа Гейгера (El Ouni, Ben Kahla 2014) показана на рис. 6. Малый купол тенсегрити гейгеровского типа состоит из 32 узлов и 73 элементов: 13 вертикальных стоек (пронумерованных от 1 до 13) и 60 струн (пронумерованных от 14 до 73). Граничные условия были выбраны таким образом, чтобы ограничивать движение узлов 7, 12, 17, 22, 27 и 32 во всех направлениях (X, Y и Z). Следовательно, структура имеет 78 степеней свободы, определяемых следующим образом: три степени свободы на каждый внутренний узел в порядке X, Y, затем Z. Координаты всех узлов приведены в таблице 5.
Все элементы имеют модуль упругости 1,6·1011 Н/м2 и плотность 7,85·103 кг/м3. Площадь поперечного сечения стоек равна 10–4 м2. Площадь поперечного сечения и начальное предварительное натяжение элементов кабеля приведены в табл. 6. Возбуждение конструкции осуществляется белым шумом. Для идентификации доступны измерения только пяти датчиков и частота дискретизации fs = 30 Гц.
The same spectral analysis procedure used for the tripod simplex structure to validate system identifcation is employed for the Geiger dome. In Figures 7–11, five spectra are presented and compared with the spectra obtained by the application of FFT to measurements. These comparisons show clearly that the parameters of the structure model are well identifed since the data spectra and the model ft despite the divergence that appeared in all the cross spectrum and the autospectrum of sensor 3.
Для купола Гейгера используется та же процедура спектрального анализа, что и для конструкции треноги, для проверки правильности идентификации системы. На рис. 7–11 представлены пять спектров, которые сравниваются со спектрами, полученными путём применения к измерениям БПФ. Эти сравнения ясно показывают, что параметры модели структуры хорошо идентифицируются, поскольку спектры данных и модель ft, несмотря на расхождение, появившееся во всём взаимном спектре и автоспектре с датчика 3.
При рассмотрении рис. 9 ясно видно, что все впадины и пики хорошо накладываются друг на друга, кроме впадины, близкой к частоте Найквиста (15 Гц). Эти факты позволяют сделать вывод о том, что пики идентифицируются лучше, чем долины во всех данных и модельных спектрах. На самом деле, мы можем понять это из реализации метода SSI-cov, с помощью которого нельзя гарантировать условие положительной реальной последовательности (Basseville et al. 2000). По этой причине у нас может не быть положительных расширенных ковариационных матриц. В результате расходимости спектра в этом случае вполне оправданы.
TАБЛИЦА 5. Начальные координаты узлов умного купола Гейгера
Node N° X(m) Y(m) Z(m) Node N° X(m) Y(m) Z(m)
1 0 0 0.21 17 –0.30 0.519615 0
2 0 0 0.15 18 –0.20 0 0.185
3 0.20 0 0.185 19 –0.20 0 0.45
4 0.20 0 0.45 20 –0.40 0 0.115
5 0.40 0 0.115 21 –0.40 0 –0.115
6 0.40 0 –0.115 22 –0.60 0 0
7 0.60 0 0 23 –0.10 –0.173205 0.185
8 0.10 0.173205 0.185 24 –0.10 –0.173205 0.45
9 0.10 0.173205 0.45 25 –0.20 –0.346410 0.115
10 0.20 0.346410 0.115 26 –0.20 –0.346410 –0.115
11 0.20 0.346410 –0.15 27 –0.30 –0.519615 0
12 0.30 0.519615 0 28 0.10 –0.173205 0.185
13 –0.10 0.173205 0.185 29 0.10 –0.173205 0.45
14 –0.10 0.173205 0.45 30 0.20 –0.346410 0.115
15 –0.20 0.346410 0.115 31 0.20 –0.346410 –0.115
16 –0.20 0.346410 –0.115 32 0.30 –0.519615 0
ТАБЛИЦА 6. Площадь поперечного сечения и начальное предварительное натяжение различных семейств тросов купола Гейгера.
Cable family Cable number Cross-section area (10–4m2) Initial pre-tension (KN) Initial pre-stress (MPa)
1 14–19 0.01 0.20 200
2 20–25 0.01 0.144 144
3 26–31 0.02 0.519 259.5
4 32–37 0.02 0.519 259.5
5 38–43 0.04 1.304 326
6 44–49 0.04 1.304 326
7 50–55 0.01 0.15 150
8 56–61 0.02 0.48 240
9 62–67 0.01 0.15 150
10 68–73 0.04 1.13 282.5
FFT vs Model spectrum
Data
100 Model
10–5
0 5 10 15
Frequencies (Hz)
Corrélations Empirique vs Théorique
0.4
0.2
0
–0.2
–0.4
0 20 40 60 80 100 120 140
Time Log index
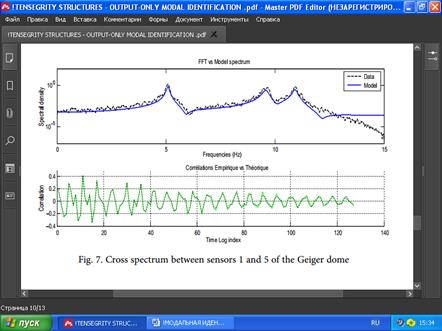
РИС. 7. Взаимный спектр с датчиков 1 и 5 купола Гейгера
.
0 Spectres Empirique vs Théoriques
10
Data
Model
10–5
0 5 Frequencies (Hz) 10 15
Corrélations Empirique vs Théorique
0.1
0.05
0
–0.05
–0.1
0 20 40 60 80 100 120 140
Time Log index
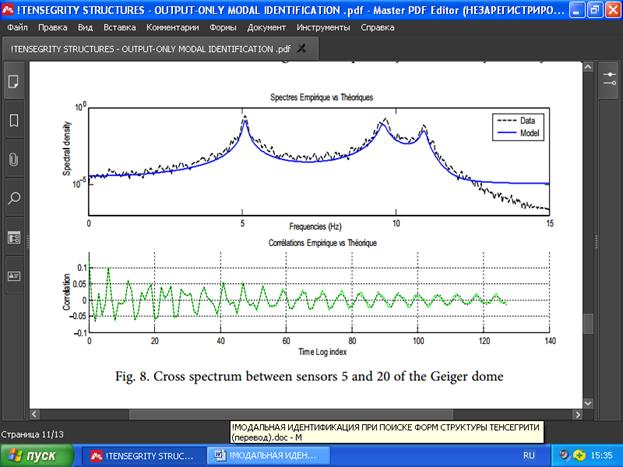
РИС. 8. Взаимный спектр с датчиков 5 и 20 купола Гейгера
Spectres Empirique vs Théoriques
Data
100 Model
10–5
0 5 Frequencies (Hz) 10 15
Corrélations Empirique vs Théorique
1
0.5
0
–0.5
0 20 40 60 80 100 120 140
Time Log index
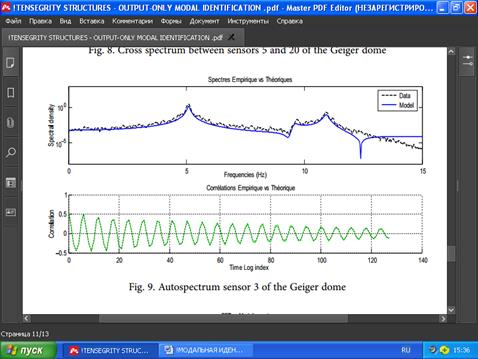
РИС. 9. Автоспектр с датчика 3 купола Гейгера
5 FFT vs Model spectrum
10
Data
Model
100
10–5
10–10
0 5 10 15
Frequencies (Hz)
Corrélations Empirique vs Théorique
1
0.5
0
–0.5
–1
0 20 40 60 80 100 120 140
Time Log index
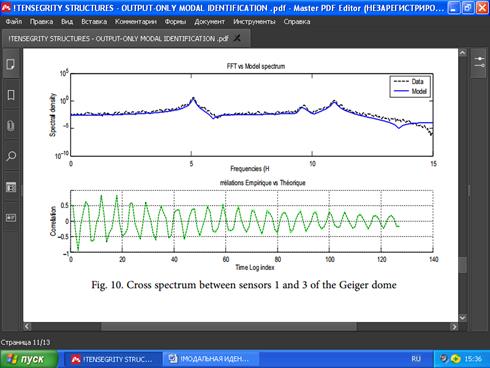
РИС. 10. Взаимный спектр с датчиков 1 и 3 купола Гейгера
ВЫВОДЫ
For tensegrity systems the structure modal signature is directly related to its state of self-stress. Thus identifying the modal parameters and monitoring their possible changes would result in the evaluation of the system internal forces and the possible detection of possible damages of its components. A simplex tensegrity structure with closely-spaced modes and a Geiger dome are considered here as an output-only modal identifcation case studies. The Balanced Realization Algorithm has been investigated for the output- only modal identifcation task. Diferent sensor locations have been studied to identify the mode shapes of tensegrity systems and their corresponding natural frequencies and damping ratios. Although the structures are considered stationeries, the BR algorithm performed quite well regarding the fact that the structure presents symmetries and therefore closely-spaced modes. Te stabilization diagram was necessary to identify close modes by imposing a high value for the MAC. When a limited number of sensors are used, it is noticed that close modes were difcult to identify.
Для систем тенсегрити модальная характеристика структуры напрямую связана с её состоянием самонапряжения. Таким образом, идентификация модальных параметров и отслеживание их возможных изменений приводит к возможности оценки внутренних сил системы и повреждений её компонентов. Простая тенсегрити-структура треноги с близко расположенными модами и купол Гейгера рассматриваются здесь как тематические исследования модальной идентификации только по выходу. Алгоритм сбалансированной реализации был исследован для задачи модальной идентификации только на выходе. Были изучены различные местоположения датчиков, чтобы определить формы колебаний систем тенсегрити и их соответствующие собственные частоты и коэффициенты демпфирования. Хотя структуры считаются стационарными, алгоритм BR работал достаточно хорошо, учитывая тот факт, что структуры симметричны и, следовательно, имеют близко расположенные моды. Диаграмма стабилизации была необходима для выявления близких мод путём установления высокого значения MAC. Было замечено, что при использовании ограниченного числа датчиков близкие моды трудно идентифицировать.
FFT vs Model spectrum
Data
0 Model
10
10–5
10–10
0 5 Frequencies (Hz) 10 15
Corrélations Empirique vs Théorique
0.5
0
–0.5
0 20 40 60 80 100 120 140
Time Log index
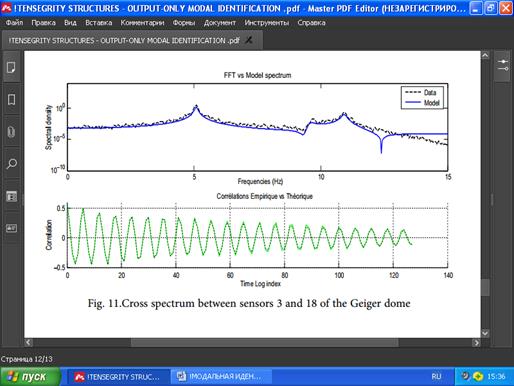
РИС. 11. Взаимный спектр от датчиков 3 и 18 купола Гейгера
ИСТОЧНИКИ
Arsenault, M.; Gosselin, C. M. 2006. Kinematic, static, and dynamic analysis of a spatial three-degree-of-freedom tensegrity mechanism, Journal of Mechanical Design 128(5): 1061– 1069. http://dx.doi.org/10.1115/1.2218881
Basseville, M. et al. 2000. Subspace-based fault detection algorithms for vibration monitoring, Automatica 36(1): 101–109. http://dx.doi.org/10.1016/S0005-1098(99)00093-X
Basseville, M., et al. 2000. Output-only subspace-based structural identification: from theory to industrial testing practice, Journal of Dynamic Systems Measurement and Control transactions of The ASME 123(4).
Bel Hadj Ali, N.; Smith, I. F. C. 2009. Dynamic analysis and vibration control of an active tensegrity structure, in J. Rodellar, E. Reithmeier (Eds.). 15th International Workshop on Dynamics and Control. Barselona.
Bel Hadj Ali, N.; Smith, I. F. C. 2010. Dynamic behaviour and vibration control of a tensegrity structure, International Journal of Solids and Structures 47(9): 1285–1296. http://dx.doi.org/10.1016/j.ijsolstr.2010.01.012
Benveniste, A.; Fuchs, J. J. 1985. Single sample modal identification of a nonstationary stochastic process, IEEE Transactions on Automatic Control 30(1): 66–74. http://dx.doi.org/10.1109/TAC.1985.1103787
Ben Kahla, N., et al. 2000. Nonlinear dynamic analysis of tensegrity systems, Journal of The International Association for Shell and Spatial Structures 41(132): 49–58.
Carden, E. P.; Mita, A. 2009. Challenges in developing confidence intervals on modal parameters estimated for large civil infrastructure with stochastic subspace identification. Structural Control & Health Monitoring. http://dx.doi.org/10.1002/stc.358
Dubé, J. F., et al. 2008. Comparison between experimental tests and numerical simulations carried out on a tensegrity mini-grid, Engineering Structures 30(7): 1905–1912. http://dx.doi.org/10.1016/j.engstruct.2007.12.010
d’Estrée Sterk, T. 2003. Using actuated tensegrity structures to produce a responsive architecture, in The 2003 Annual Conference of the Association for Computer Aided Design in Architecture, October 2003, Indianapolis, IN, USA, 85–93.
El Ouni, M. H.; Ben Kahla, N. 2014. Active tendon control of a Geiger dome, Journal of Vibration and Control 20(2): 241–255. http://dx.doi.org/10.1177/1077546312458944
Graells Rovira, A; Mirats Tur, J. 2009. Control and simulation of a tensegrity-based mobile robot, Robotics and Autonomous Systems 57(5): 526–535. http://dx.doi.org/10.1016/j.robot.2008.10.010
Giraldo, D. F., et al. 2009. Modal identification through ambient vibration: comparative study, Journal of Engineering Mechanics 135(8): 759–770. http://dx.doi.org/10.1061/(ASCE)0733-9399(2009)135:8(759)
Ingber, D. E. 1998. The architecture of life, Scientific American 278(1): 48–57. http://dx.doi.org/10.1038/scientificamerican0198-48
Juan, S. H.; Mirats Tur, J. M. 2008. A method to generate stable, collision free configurations for tensegrity based robots, in Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems 3769–3774.
Korkmaz, S.; Bel Hadj Ali, N.; Smith, I .F. C. 2011. Determining control strategies for damage tolerance of an active tensegrity structure, Engineering Structures 33(6): 1930–1939. http://dx.doi.org/10.1016/j.engstruct.2011.02.031
Korkmaz, S.; Bel Hadj Ali, N.; Smith, I. F. C. 2012. Configuration of control system for deployment and damage tolerance of a tensegrity bridge, Advanced Engineering Informatics 26(1): 145–155. http://dx.doi.org/10.1016/j.aei.2011.10.002
Magalhaes, F., et al. 2008. Operational modal analysis and finite element model correlation of the Braga Stadium suspended roof, Engineering Structures 30(6): 1688–1698. http://dx.doi.org/10.1016/j.engstruct.2007.11.010
Magalhães, F., et al. 2009. Online automatic identification of the modal parameters of a long span arch bridge, Mechanical Systems and Signal Processing 23(2): 316–329. http://dx.doi.org/10.1016/j.ymssp.2008.05.003
Masic, M.; Skelton, R. E. 2006. Selection of prestress for optimal dynamic/control performance of tensegrity structures, International Journal of Solids and Structures 43(7–8): 2110–2125. http://dx.doi.org/10.1016/j.ijsolstr.2005.06.066
Mevel, L., et al.2003. Stochastic subspace-based structural identification and damage detection– Application to the steel-quake benchmark, Mechanical Systems and Signal Processing 17(1): 91–101. http://dx.doi.org/10.1006/mssp.2002.1544
Motro, R., et al. 1986. Static and dynamic analysis of tensegrity systems, in ASCE International Symposium on Shells and Spatial Structures, Computational Aspects. New York: Springer, 270–279.
Motro, R. 2003. Tensegrity: Structural systems for the future. UK.
Murakami, H. 2001a. Static and dynamic analyses of tensegrity structures. Part II. Quasi-static analysis, International Journal of Solids and Structures 38(20): 3615–3629. http://dx.doi.org/10.1016/S0020-7683(00)00233-X
Murakami, H. 2001b. Static and dynamic analyses of tensegrity structures. Part 1. Nonlinear equations of motion, International Journal of Solids and Structures 38(20): 3599–3613. http://dx.doi.org/10.1016/s0020-7683(00)00232-8
Sultan, C., et al. 2002. Linear dynamics of tensegrity structures, Engineering Structures 24(6): 671–685. http://dx.doi.org/10.1016/S0141-0296(01)00130-4
Peeters, B.; Ventura, C. E. 2003. Comparative study of modal analysis techniques for bridge dynamic characteristics, Mechanical Systems and Signal Processing 17(5): 965–988. http://dx.doi.org/10.1006/mssp.2002.1568
Puig, L., et al. 2010. A review on large deployable structures for astrophysics missions, Acta Astronautica 67(1–2): 12–26. http://dx.doi.org/10.1016/j.actaastro.2010.02.021
Paul, C., et al. 2006. Design and control of tensegrity robots for locomotion, IEEE Transactions on Robotics 22(5): 944–957. http://dx.doi.org/10.1109/TRO.2006.878980
Reynders, E., et al. 2007. Uncertainty bounds on modal parameters obtained from stochastic subspace identification, Mechanical Systems and Signal Processing 22(4): 948–969. http://dx.doi.org/10.1016/j.ymssp.2007.10.009
Skelton, R. E., et al. 2001. An introduction to the mechanics of tensegrity structures, in Proceedings of the 40th IEEE Conference on Decision and Control 4255: 4254–4259. Orlando, Florida USA. http://dx.doi.org/10.1109/cdc.2001.980861
Skelton, R. E.; de Oliveira, M. C. 2009. Tensegrity systems. Springer.
Van Overchee, P.; De Moor, B. 1996. Subspace identification for linear systems: theory, implementation, applications. The Netherlands: Kluwer Academic Publishers. http://dx.doi.org/10.1007/978-1-4613-0465-4
ОБ АВТОРАХ
Miniar ATTIG. Currently a PhD student at the Dept of Civil Engineering of the National School of Engineering of Tunis (ENIT), Tunisia, from which she obtained a Master of Science in structural engineering. She is a member of the Laboratory of Systems and Applied Mechanics, Polytechnic School of Tunisia, La Marsa, Tunisia. Research interests: Cable dynamics, non-linear static and dynamic analysis of cable structures, tensegrity structures, active control of fexible structures.
Миниар АТТИГ. В настоящее время аспирант кафедры гражданского строительства Национальной инженерной школы Туниса (ENIT), Тунис, где она получила степень магистра наук в области проектирования конструкций. Она является членом Лаборатории систем и прикладной механики Политехнической школы Туниса, Ла-Марса, Тунис. Область научных интересов: вантовая динамика, нелинейный статический и динамический анализ вантовых конструкций, тенсегрити-конструкции, активное управление подвижными конструкциями.
Maher ABDELGHANI. Assoc. Prof. at the Dept of Mechanical Engineering of the Higher Institute of Applied Sciences and Technologies of Sousse, University of Sousse Tunisia. He obtained his PhD degree from the University of Montpellier II, France, He is a member of the Laboratory of Systems and Applied Mechanics, Polytechnic School of Tunisia, La Marsa, Tunisia. Research interests: structural dynamics, structural health monitoring, system modelling and identifcation, advanced control theory.
Махер АБДЕЛЬГАНИ. доц. Профессор кафедры машиностроения Высшего института прикладных наук и технологий Сусса Университета Сусса, Тунис. Он получил степень доктора философии в Университете Монпелье II, Франция. Он является членом Лаборатории систем и прикладной механики Политехнической школы Туниса, Ла-Марса, Тунис. Научные интересы: структурная динамика, мониторинг состояния конструкций, моделирование и идентификация систем, современная теория управления.
Nabil ben KAHLA. Currently an Assoc. Prof. at the Dept of Civil Engineering of King Khalid University, Abha, Kingdom of Saudi Arabia. He obtained his PhD degree from the University of Wisconsin-Madison, USA. He is a member of the Laboratory of Systems and Applied Mechanics, Polytechnic School of Tunisia, La Marsa, Tunisia. He is the author of several scientifc papers. Research interests: non-linear cable dynamics, guyed masts, tensegrity structures, discrete element methods, active and passive control of fexible structures.
Набиль бен КАЛА. В настоящее время доц. Профессор кафедры гражданского строительства Университета короля Халида, Абха, Королевство Саудовская Аравия. Он получил степень доктора философии в Университете Висконсин-Мэдисон, США. Он является членом Лаборатории систем и прикладной механики Политехнической школы Туниса, Ла-Марса, Тунис. Он является автором нескольких научных работ. Область научных интересов: нелинейная вантовая динамика, мачты с оттяжками, тенсегрити-структуры, методы дискретных элементов, активное и пассивное управление подвижными конструкциями.








