Рис. 3. Пример 1 : двухступенчатая структура тенсегрити (тип 1). а) Вид сверху , б) вид сбоку и в) вид в перспективе.
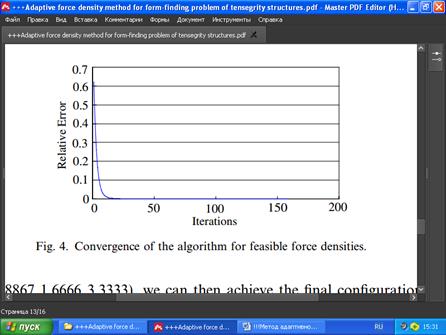
Рис. 4. Сходимость алгоритма при допустимых плотностях сил.
Пример 2. Поскольку начальные плотности сил и независимые узловые координаты могут быть произвольно заданы проектировщиком, мы можем иметь некоторый контроль над геометрическими и механическими свойствами конструкции. Кроме того, путём изменения значений начальных плотностей сил и узловых координат могут быть легко найдены новые конфигурации. Например, если координата x узла d изменена с 1,8867 на 2,8867 без изменения других параметров, то мы получим новую конфигурацию той же двухступенчатой структуры тенсегрити, показанную на Рис. 5. Для поиска новых конфигураций можно также изменять начальные плотности сил на первом шаге Алгоритма 1.
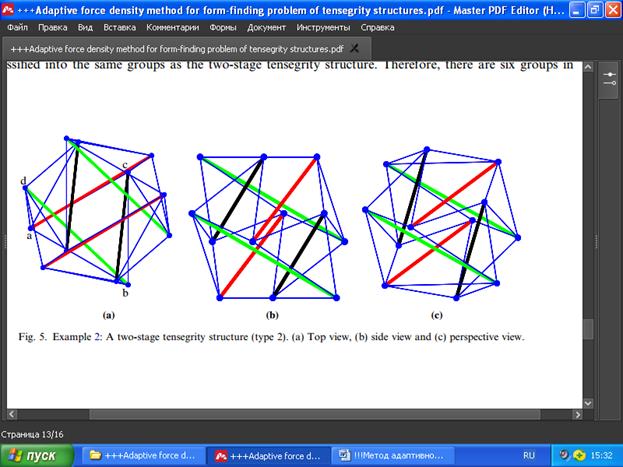
Рис. 5. Пример 2: двухступенчатая структура тенсегрити (тип 2). а) Вид сверху, б) вид сбоку и в) вид в перспективе.
Ошибки проектирования n, определённые из (48) для примеров 1 и 2, меньше 10-13. Обе структуры, полученные в Примерах 1 и 2, имеют только один бесконечно малый механизм и один режим самонапряжения ; т.е. они кинематически и статически неопределимы (Пеллегрино и Калладайн, 1986). В то же время матрица геометрической жёсткости в обоих случаях является положительно полуопределённой, т.е. полученные структуры сверхустойчивы. Итак, как ясно из этих примеров,
введение предварительного напряжения придаёт жёсткость бесконечно малому механизму, делая структуры устойчивыми.
5.2. Трёхступенчатая структура тенсегрити
Метод адаптивной плотности сил применим к структурам с гораздо большим числом элементов. Рассмотрим сложную трёхступенчатую структуру, имеющую верхнюю, центральную и нижнюю ступени. Стойки классифицированы на две группы: 1) шесть стоек на верхней и нижней ступенях и (2) три стойки на центральной ступени, а тросы классифицируются на те же группы, что и в двухступенчатой структуре выше. Таким образом, итого существует шесть групп.
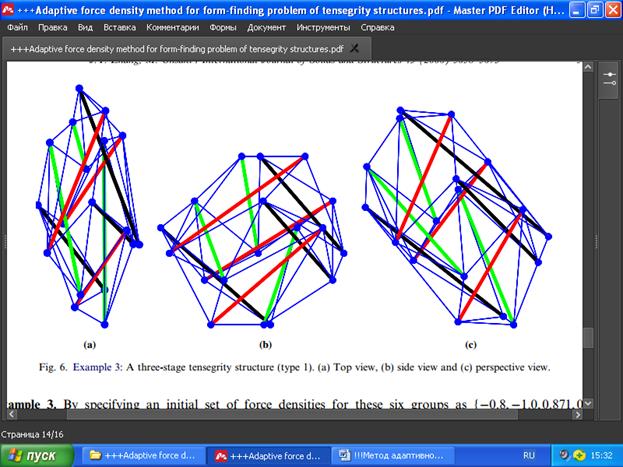
Рис. 6. Пример 3: трёхступенчатая структура тенсегрити (тип 1).
а) Вид сверху , б) вид сбоку и в) вид в перспективе.
Пример 3. При задании начального набора плотностей сил для этих шести групп как (0.8, 1.0, 0.871, 0.3, 0.7244, 0.5} с указанием координат узлов в нижней базе и нижнего узла в центральной ступени как (-2.6667, 0.0, 0.0), (1.3333, -2.3094, 0.0), (1.3334, 2.3094, 0.0)} и (-1.8867, 1.6666, 3.3333) соответственно, в результате мы получаем конфигурацию трёхступенчатой структуры тенсегрити, изображённой на рис. 6. Видно, что эта структура асимметрична, хотя мы задали симметричные плотности сил для элементов, прежде разделив их на шесть групп.
Пример 4. Вместо того, чтобы присваивать значение 0 h* наименьшим собственным значениям E, присвоим значение 0 его h* наименьшим абсолютным значениям (начальные плотности сил и независимые узловые координаты такие же, как в примере 3). Конфигурация структуры для этого случая показана на рис. 7.
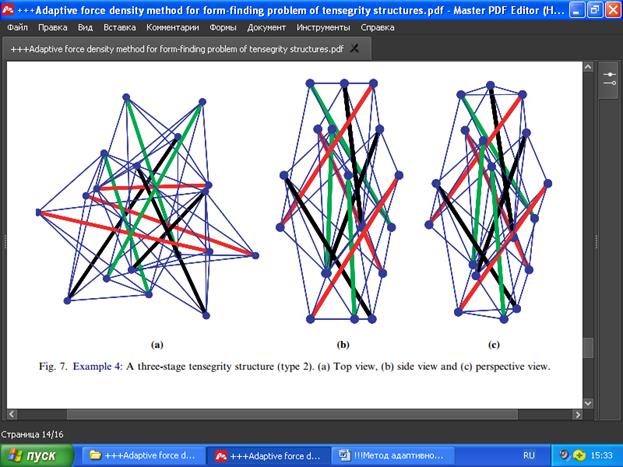
Рис. 7. Пример 4: трёхступенчатая структура тенсегрити (тип 2).
а) Вид сверху, б) вид сбоку и в) перспектива .
Обе из трёхступенчатых структур в примерах 3 и 4 имеют один бесконечно малый механизм и один режим самонапряжения, следовательно, они кинематически и статически неопределимы.
Здесь представлены не все результаты проведённых обширных численных экспериментов для проверки нового метода поиска форм. Все они показывают, что путём соответствующих изменений начальных плотностей сил и узловых координат элементов могут быть систематически найдены новые конфигурации.
6. Обсуждения и выводы
Был представлен метод адаптивной плотности сил для определения формы структур тенсегрити, основанный на анализе собственных значений при спектральном разложении матрицы равновесия относительно узловых координат. В формулировку метода могут быть включены линейные ограничения на некоторые удельные плотности сил и заданы состояния предварительного напряжения для каждого элемента так, как ожидалось; т.е. натяжение для тросов и сжатие для распорок. Вектор плотности сил обновляется на основе решения по методу наименьших квадратов, определяемого матрицей равновесия и заданными линейными ограничениями. После получения возможного набора плотностей силы, для которых соответствующая матрица равновесия имеет требуемый недостаток ранга, может быть задан независимый набор узловых координат, чтобы сгенерировать новую уникальную и невырожденную конфигурацию заданной структуры.
Было обсуждено требование недостатка ранга матрицы равновесия для получения невырожденной структуры тенсегрити, даны формулировки касательной, линейной и геометрической матриц жёсткости, что применимо для любого типа штифтовых соединений в конструкциях. Показано, что матрице равновесия соответствует геометрическая матрица жёсткости в традиционной формулировке метода конечных элементов.
В численных примерах продемонстрирована очень хорошая сходимость алгоритма. Это также показывает, что предложенный подход обладает очень хорошими возможностями для поиска новых невырожденных конфигураций лишь при изменениях значений начального набора плотностей силы на первом шаге и узловых координат на последнем шаге процедуры поиска формы.
Однако, предлагаемый способ не может дать прямого и точного контроля над геометрическими и механическими свойства структуры, поскольку параметрами метода являются не силы и не длины, а отношения силы к длине, т.е. плотности сил. Поэтому, как было показано ещё Тибертом и Пеллегрино (2003), с помощью предлагаемого метода при симметричном наборе плотностей силы могут быть найдены асимметричные конфигурации, поскольку длины элементов не описываются явно и линейно (геометрическая нелинейность при физической линейности элементов).
Источники
Борс, Г.Дж., 1997. Численные методы с помощью MATLAB. Международное издательство Thomson, Inc.
Коннелли, Р., 1999.
Структуры Тенсегрити: почему они стабильны? В: Торп, Даксбери (Ред.),Теория жесткости и приложения.Kluwer/
Издатели Пленума, стр. 47-54.
Коннелли, Р., Террелл, М., 1995. Глобально жесткие симметричные тензогенности. Структура. Топология 21, 59-78.
Фуллер, Р.Б., 1975. Синергетика, исследования в Геометрии мышления. Кольер Макмиллан, Лондон, Великобритания.
Гость, С., 2006. Жесткость предварительно напряженных каркасов: объединяющий подход. Int. J.Структура твердых тел. 43, 842-854.
Ханаор, А., 1988. Предварительно напряженные штифтовые конструкции- анализ гибкостии проектирование предварительного напряжения. Вычислительная структура. 28 (6), 757-769.
Кавех, А., 2004. Структурная механика:методы графа и матрицы , третье изд. Издательство "Исследовательские исследования ", Сомерсет, Великобритания.
Linkwitz, K., Schek, H.-J., 1971. Einige Bemerkungen zur Berechnung von vorgespannten Seilnetzkonstruktionen. Изобретатель-Архив. 40, 145–158.
Мазич, М., Скелтон, Р.Э., Джилл, П.Э., 2005. Алгебраический поиск формы тенсегрити . Int. J.Структура твердых тел. 42, 4833-4858.
Мотро, Р., 1996. Структурная морфология систем тенсегрити . Инт. J. Пространственная структура. 11 (1 и 2), 233-240.
Мотро, Р., Наджари, С., Джоанна, П., 1986. Статический и динамический анализ систем тенсегрити . В: ТрудыМеждународного
Симпозиум по оболочкам и пространственным структурам: вычислительные аспекты. Спрингер, Нью-Йорк, стр. 270-279.
Мураками, Х., 2001. Статический и динамический анализ структур тенсегрити . Часть 1. Нелинейные уравнения движения. Int. J.Структура твердых тел. 38, 3599–3613.
Пеллегрино, С., Калладайн, К.Р., 1986. Матричный анализ статически и кинематически неопределенных структур. Int. J. SolidsStruct. 22, 409–428.
Сайто, М., Окада, А., Табата, Х., 2001. Исследование на эти структурные характеристики из тенсегрити стропильные арки. В:Материалы IASS 2001 г., Нагоя, Япония.
Щек, Х.-Дж., 1974. Метод плотности силы для нахождения формы и вычисления сетей общего назначения. Вычислить. Методы, Применяемые. Механик. Англ. 3, 115–134.
Султан, К., Корлесс, М., Скелтон, Р.Э., 2002. Симметричная реконфигурация структур тенсегрити . Инт. J.Структура твердых тел.39, 2215-2234.
Тиберт, А.Г., Пеллегрино, С., 2003. Обзор методов определения формыдляструктур тенсегрити . Int. J. Space Struct. 18 (4), 209-223.
Дж.Я. Чжан, М. Осаки / Международный журнал по твердымтелам и структурам 43 (2006) 5658-56735673
Вассарт Н., Мотро Р., 1999. Многопараметрическийметод определения формы : применение ксистемам тенсегрити. Int. J.Пространственная структура. 14 (2), 147–154.
Ван, Б.Б., 1996. Новый тип самонапряженной уравновешивающей систему трос-распорка, изготовленную из взаимно направленных призм. Int. J. Space Structure. 11,,, 357-362.
Чжан, Дж.Й., Осаки, М., Канно, Й., 2006. Прямой подход к проектированию геометрии и сил систем тенсегрити . Int. J.Структуратвердых тел. 43 (7–8).
ENGINEERING STRUCTURES AND TECHNOLOGIES
ISSN 2029-882X /eISSN 2029-8838
2016 8(2): 52–64
doi:10.3846/2029882X.2016.1175323








