Алгоритм 2. Метод адаптивной плотности сил
Шаг 0: Задаётся топология структуры.
Шаг 1: Указываются линейные ограничения и начальный набор значений плотности сил.
Шаг 2: Находится допустимый набор плотностей сил путем реализации Алгоритма 1.
Шаг 3: Находится независимый набор узловых координат, определяющий уникальную и невырожденную конфигурацию самонапряжённой структуры.
5. Численные примеры
Для демонстрации надёжности и способности поиска новых конфигураций по предлагаемому методу представлены численные примеры нахождения нескольких структур тенсегрити с использованием MATLAB версии 6.5.1 (Borse, 1997).
5.1. Двухступенчатая структура (призма) тенсегрити
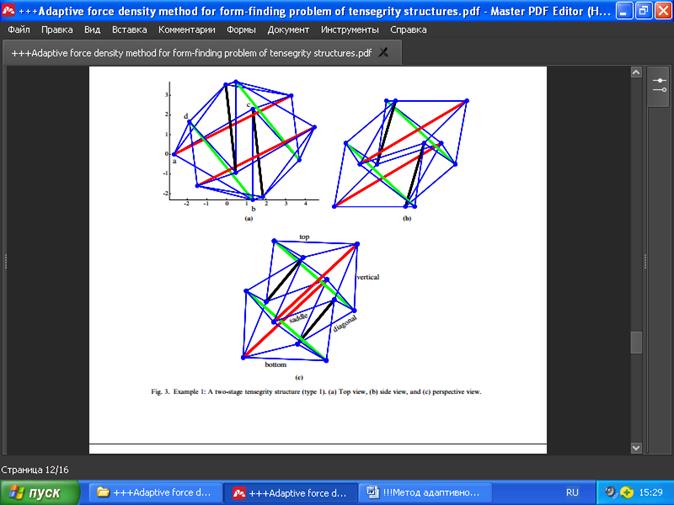
Сначала применим предлагаемый метод для расчёта структуры тенсегрити на Рис. 3. Конструкция состоит из 12 узлов и 30 элементов, т.е. n = 12, m = 30. Её шесть стоек разделены на две группы: 1) стойки верхней ступени и 2) стойки нижней ступени. 24 кабеля разделены на 3) верхнее и нижнее основания, (4) седловину, (5) вертикаль и (6) диагональ (Sultan et al., 2002), как показано на рис. 3c.
Пример 1. По заданному начальному набору плотностей сил {1.5, -1.5, 1.0, 2.0, 1.0, 1.0} для указанных шести групп Алгоритм 1 находит допустимый набор плотностей силы {1.8376, -1.8376, 0.9281, 1.9918, 1.1737, 0.9958} на 158-й итерации. Относительная погрешность нахождения вектора плотности сил на каждой итерации определяется как евклидова норма разности текущего qi и конечного q^ значений, что показано на рис. 4. Условием завершения алгоритма 1 является требуемый дефицит ранга h* = n – ранг(E) = 4 матрицы равновесия Е при │λh*│<10-5 и │λh*+1│>10-5. На рис.4 можно видеть очень хорошую сходимость Алгоритма 1, посколькуотносительная погрешность очень близка к нулю всего после 20 итераций.
Если задать координаты узлов a, b и c нижнвй базы на плоскости x-y (рис.3а) равными (-2.6667, 0.0, 0.0), (1.3333, -2.3094, 0.0) и (1.3334, 2.3094, 0.0) соответственно и координаты узла d в нижней ступени как (1.8867, 1.6666, 3.33333), то можно получить окончательную форму структуры на рис. 3.