[53] Kia Yick Tan. The computer design of tensile membrane structures. 1989.
[54] Gunnar Tibert. Deployable tensegrity structures for space applications. PhD thesis,
KTH, 2002.
[55] Brian R Tietz, Ross W Carnahan, Richard J Bachmann, Roger D Quinn, and Vytas Sun-
Spiral. Tetraspine: Robust terrain handling on a tensegrity robot using central pat-
tern generators. In 2013 IEEE/ASME International Conference on Advanced Intelligent
Mechatronics, pages 261–267. IEEE, 2013.
[56] G.A. Tournois. Tensegrity locomotion on rough terrain. diploma thesis, Delft Univer-
sity of Technology, June 2017.
[57] Hoang Chi Tran and Jaehong Lee. Form-finding of tensegrity structures with multiple
states of self-stress. Acta mechanica, 222(1-2):131, 2011.
[58] Andreas Wächter and Lorenz T Biegler. Line search filter methods for nonlinear pro-
gramming: Local convergence. SIAM Journal on Optimization, 16(1):32–48, 2005.
[59] Lianjun Wu, Monica Jung de Andrade, Tarang Brahme, Yonas Tadesse, and Ray H
Baughman. A deformable robot with tensegrity structure using nylon artificial muscle.
In SPIE Smart Structures and Materials+ Nondestructive Evaluation and Health Moni-
toring, pages 97993K–97993K. International Society for Optics and Photonics, 2016.
[60] Michael C Yip and Günter Niemeyer. On the control and properties of supercoiled
polymer artificial muscles. IEEE Transactions on Robotics, 2017.
[61] Xingfei Yuan, Xiaotian Liang, and Along Li. Shape and force control of prestressed
cable-strut structures based on nonlinear force method. Advances in Structural Engi-
neering, 19(12):1917–1926, 2016.
[62] JY Zhang and M Ohsaki. Adaptive force density method for form-finding problem of
tensegrity structures. International Journal of Solids and Structures, 43(18-19):5658–
5673, 2006.
Приложение А. Метод нулевого пространства
Здесь описана процедура с нулевым пространством, основанная на реализациях Gill et al. [16] и Nocedal & Wright [39]. Он используется для решения системы KKT на каждой итерации метода активного набора. Учитывая следующую систему KKT квадратичной программы
· ¸· ¸ · ¸
G −C p a
T = − , (A.1)
−C 0 v b
где C - матрица n × m с полным рангом столбца. По определению QR - декомпозиция C
является
· ¸ · ¸
R £ ¤ R
C = Q = Y Z , (A.2)
0 0
где Z − матрица n × (n - m) нулевого пространства C , а Y - любаяматрица n × m , обеспечивающая, чтобы Q было
неособый. Этот метод не требует, чтобы матрица Гессе G была неособой. Позвольте нам
предположим , что вектор p может быть разделен
p = Ypy + Zpz . (A.3)
T
Если мы подставим это в (A.1) и используем тот факт, что C Z = 0 согласно Z , являющемуся нулевым пространством
C. Теперь второе уравнение становится
T
C Ypy = b , (A.4)
где py может быть получено путем обратной подстановки из- за вышеупомянутого полного ранга и
неособые свойства C и Y. Второе уравнение системы KKT имеет вид
GYpy + GZpz − Cv = −a . (A.5)
Т Т
Если мы умножим на Z и снова воспользуемся тем фактом, что C Z = 0, мы получим
47
48 A. Метод с нулевым пробелом
¡ ¢ ¡ ¢
Т Т
Z GZ pz = −Z GYpy + a . (A.6)
теперь, когда мы знаем py, для pz можно решить с помощью факторизации Холецкого приведенных Hes-
T
сианская матрица Z GZ. Приведенный гессиан положительно определен, что обеспечивает локальные оптимумы.
T
Наконец, чтобы получить v , мы умножаем первое уравнение (A.1) на Y :
Т Т Т,Т
Y Cv = Y GYpy + Y GZ p z + Y a (A.7)
¡ ¢
Т Т
⇒ Y Cv = Y Gp + a (A.8)
£ ¤Т
который опять же может быть решен с помощью обратной замены. Теперь вектор p vполучен
на чем завершается эта процедура с нулевым пробелом.
Приложение В. Исполнительные механизмы
Здесь описывается эксперимент, показывающий физические ограничения используемых в роботах тенсегрити исполнительных механизмов. В качестве примера рассматриваются скрученные полимерные мышцы (TCPM), которые имеют хорошую применимость в стрессовых ситуациях, поскольку могут служить не только в качестве исполнительных механизмов, но и использоваться как пассивные конструктивные элементы. TCPM также показали низкую производственную стоимость, отсутствие отклонений в работе и высокий цикл жизни [21]. Эксперименты показали, что для них максимальный ход растяжения может превышать таковой для скелетных мышц in vivo примерно на 20% [21, 35]. Однако известно, что TCPM имеют низкую скорость сжатия и низкую эффективность с точки зрения теплового приведения в действие [8].
Как правило, существует два типа скрученных и намотанных
полимерные мышцы, которые отличаются способом получения спиралей в предшественнике
волокно (нейлоновое волокно):
• Автоматическая намотка: вставка скрутки в волокно-предшественник для достижения намотки за счет механического-
нестабильность кал
• Намотка оправки: вставка скрутки в исходное волокно до тех пор, пока механическая стабильность-
достигается плотность, затем волокно оборачивают вокруг оправки
Чтобы иметь представление об ограничениях TCPM в практическом применении, давайте поближе рассмотрим человека-
дрел напряг мускулы. Известно, что они имеют определенные ограничения в зависимости от производства
способ, выбор материала, средства приведения в действие и геометрия. Спиральные мышцы оправки
имеют меньшую грузоподъемность по сравнению с автоматической намоткой, но могут достигать большего хода
из-за расстояния между соседними катушками [21]. Был проведен эксперимент , чтобы определить-
увеличьте усилие для намотанной на оправку мышцы с помощью Джоулева нагрева. Для данного
потребляемая мощность TCPM достигнет установившегося значения, когда внутренняя скорость нагрева
соответствует внешней скорости охлаждения [60]. Если заданная установившаяся температура превышает
температура теплового отклонения волокна-предшественника TCPM поврежден. Если бы кто - то должен был
примените мышцу, свернутую спиралью на оправке, в роботе tensegrity, было бы полезно включить безопасность
ограничения исполнительного механизма в стратегии управления. В этом разделе описан способ производства
описан TCPM, обернутый оправкой. Далее рассказываются подробности эксперимента и, наконец,
результаты интерпретируются.
49
50 B. Приводы
B.1. Производство скрученных и намотанных полимерных мышц.
TCPM изготовлен из двух материалов: нейлонового волокна 6 длиной 1 м и диаметром 0,6 мм и железный провод сопротивления такой же длины и диаметром 0,2 мм. Волокно и проволока связаны вместе с обоих концов. Один конец прикреплен к поворотному механизму, приводимому в движение сверлильным машины, а другой - к грузу весом 300 г, который подвешивается в воздухе с помощью системы шкивов.
Это создает под действием гравитационных сил постоянное натяжение в волокне и проволоке, что предотвращает запутывания волокон и проводов сопротивления.
Далее, приводится в движение скручивающий привод для закручивания вставки до тех пор, пока не произойдет автоматическая намотка, то есть когда максимум достигается количество витков на единицу длины. Затем скрученное волокно и проволоку наматывают на оправку, сохраняя при этом- упомянутое напряжение приложено. Направление обертывания определяет, будет ли мышца быть гомохиральным или гетерохиральным. При нагревании гомохиральные мышцы сокращаются, но гетерохиральные- ral удлиненный [8]. Для этого проекта были созданы гомохиральные мышцы. Диаметр катушки из получаемая мышца определяется диаметром оправки. После того, как волокно и проволока были надежно завернутые и прикрепленные к оправке, они подвергаются термическому отжигу. Отжиг выполняется следующим образом:
◦
- Один час в традиционной духовке при температуре 155 ° C.
◦
- Один час в традиционном холодильнике при температуре 6 ° C.
B.2. Эксперимент
Оборудование , используемое в этом эксперименте:
- Тестер растяжения Mark-10 с датчиком усилия.
- Источник питания CALTEK PSA30/3B.
- Один TCPM, изготовленный по описанной технологии.
- Печатная плата для управления током.
Мышца приводится в действие при изометрическом напряжении, т.е. её длина сохраняется постоянной, пока она С джоулевым нагревом. Смещение d варьируется от 20 до 55 мм с шагом 5 мм. Первый мышца помещается в тестер на растяжение в расслабленном состоянии. Затем его растягивают до нужного смещению и дали отдохнуть в течение 180 секунд, чтобы смягчить динамические эффекты. Наконец, 12 V прямой ток подается при 30%-ном рабочем цикле в течение 120 секунд, эта процедура повторяется при 60%-ном рабочем цикле Цикл. Данные о силе собираются с помощью датчика силы тестера на растяжение.
B.3. Экспериментальные результаты
Рисунки B.1a-B.1b показывают измерения усилия для 30% рабочего цикла и 60% рабочего цикла re-умозрительно. Как можно наблюдать, после определенного джоуля происходит насыщение изменения силы- Своевременное включение отопления. Можно также заметить, что при 30% рабочем цикле усилие действительно достигается стационарный режим, тогда как для 60% рабочего цикла кривая усилия существенно колеблется. В таблице B.1 показано максимальное изменение усилия, достигаемое Джоулевым нагревом при нагрузке 30%.
Цикл и рабочий цикл 60% при постоянном токе 12 В. Как можно видеть, большее изменение в силе достигается при большем рабочем цикле. Максимальное изменение при 30% рабочем цикле составляет 0,068 Н и 0,093 Н при рабочем цикле 60%.
Таблица B.1. Максимальные изменения усилия, достигаемые при джоулевом нагреве TCPM
Рабочий цикл 30% при 12 В
d (в мм) 20 25 30 35 40 45 50 55
δFm (в N) 0,068 0,059 0,056 0,056 0,057 0,053 0,053 0,049
Рабочий цикл 60% при 12 В
d (в мм) 20 25 30 35 40 45 50 55
δFm (в N) 0,087 0,093 0,089 0,085 0,064 0,069 0,072 0,077
B. Приводы
a. Рабочий цикл 30%
b. Рабочий цикл 60%
Рисунок B.1. Зависимость усилия от времени для TCPM с джоулевым нагревом при различном перемещении.
Приложение С. Проверка повторяемости результатов.
В этом приложении подробно описывается проверка метода на повторяемость. Для определения повторяемости метод был запущен десять раз с одними и теми же входными переменными, т.е. с фиксированным набором настроек параметров, запуск- изменение конфигурации и траектории для отслеживания. Цель состояла в том, чтобы достичь одного и того же результата каждый запустите, чтобы подтвердить детерминированный характер метода. Входные переменные были установлены, как определено в Таблица 4.2 и отслеживаемые переменные результата были нулевыми. итераций, множители Лагранжа- ошибки, значения целевой функции и ограничения. Отслеживаемая траектория была той , которую видели на рисунке 4.2. Используемые ограничения были определены для ограничения центра масс конструкции в пределах своей базы поддержки. Для каждого из десяти заездов траектория была разделена на 250 шагов. Как можно видеть на рисунке C.1 для этой отслеживаемой траектории активно только ограничение 2. Как и ожидалось, через десять трасс при том же наборе входных переменных выходные результаты действительно были одинаковыми, подкрепляя детерминированный характер алгоритма. Таблица, в которой сравниваются результаты для каждого шага по все запуски можно увидеть в Приложении C. В этих таблицах приведены значения для шагов, на которых ограничения были активны.
Основание опоры - Вид сверху
0.1 Множители Лагранжа
БоС 1
CoM 2
0.9
0.8
0.05 0.7
0.6
0.5
0 0.4
0.3
0.2
0.1
-0.05
-0.04 -0.02 0 0.02 0.04 0.06 0.08 0.1 0
x-положение в м 0 50 100 150 200 250
Шаг
a. Траектория CoM вдоль отслеживаемого
b. Соответствующий множитель Лагранжа.
траектория. Отображение действующих ограничений.
Рисунок C.1. Результаты однократного запуска для проверки обеспечения повторяемости (отображение отслеживаемой траектории и активация ограничений).
Следующие таблицы содержат переменные; ошибка ограничения, значение целевой функции, La-значение множителя grange и количество итераций учитываются как для метода SQP, так и для метода active set.
Таблица C.1. Ошибка ограничения при 10 запусках (только для оактивного ограничения g 2 ).
Запускает
0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00
0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00
0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00
0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00
0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00
0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00
-3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18-3.47E-18-3.47E-18-3.47E-18-3.47E-18-3.47E-18
-3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18-3.47E-18-3.47E-18-3.47E-18-3.47E-18-3.47E-18
0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00
0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00
-3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18-3.47E-18-3.47E-18-3.47E-18-3.47E-18-3.47E-18
-6.94E-18 -6.94E-18 -6.94E-18 -6.94E-18 -6.94E-18 -6.94E-18 -6.94E-18 -6.94E-18 -6.94E-18 -6.94E-18-6.94E-18-6.94E-18-6.94E-18-6.94E-18-6.94E-18
0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00
0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00
0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00
0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00
Шаги
-3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18-3.47E-18-3.47E-18-3.47E-18-3.47E-18-3.47E-18
0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00
0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00
0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00
0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00
0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00
0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00
0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00
-3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18-3.47E-18-3.47E-18-3.47E-18-3.47E-18-3.47E-18
-3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18-3.47E-18-3.47E-18-3.47E-18-3.47E-18-3.47E-18
0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00
0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00
0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00
-6.94E-18 -6.94E-18 -6.94E-18 -6.94E-18 -6.94E-18 -6.94E-18 -6.94E-18 -6.94E-18 -6.94E-18 -6.94E-18-6.94E-18-6.94E-18-6.94E-18-6.94E-18-6.94E-18
-3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18-3.47E-18-3.47E-18-3.47E-18-3.47E-18-3.47E-18
-3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18 -3.47E-18-3.47E-18-3.47E-18-3.47E-18-3.47E-18-3.47E-18
55
Таблица C.2. Значения целевой функции за 10 запусков ( только при активном ограничении).
.
Запускает
2.12E-06 2.12E-06 2.12E-06 2.12E-06 2.12E-06 2.12E-06 2.12E-06 2.12E-06 2.12E-06 2.12E-06 В-06
1.52E-04 1.52E-04 1.52E-04 1.52E-04 1.52E-04 1.52E-04 1.52E-04 1.52E-04 1.52E-04 1.52E-04 и 1.52E-04 и 1.52E-04
1.40E-04 1.40E-04 1.40E-04 1.40E-04 1.40E-04 1.40E-04 1.40E-04 1.40E-04 1.40E-04 1.40E-04 В-04 1.40
1.30E-04 1.30E-04 1.30E-04 1.30E-04 1.30E-04 1.30E-04 1.30E-04 1.30E-04 1.30E-04 1.30E-04 ВР 1.30E-04
1.20E-04 1.20E-04 1.20E-04 1.20E-04 1.20E-04 1.20E-04 1.20E-04 1.20E-04 1.20E-04 1.20E-04 и 1.20E-04 и 1.20E-04
1.11E-04 1.11E-04 1.11E-04 1.11E-04 1.11E-04 1.11E-04 1.11E-04 1.11E-04 1.11E-04 1.11E-04-1.11E-04-1.11E-04
1.02E-04 1.02E-04 1.02E-04 1.02E-04 1.02E-04 1.02E-04 1.02E-04 1.02E-04 1.02E-04 1.02E-04 и 1.02E-04-04
9.43E-05 9.43E-05 9.43E-05 9.43E-05 9.43E-05 9.43E-05 9.43E-05 9.43E-05 9.43E-05 9.43E-05 и 9.43E-05 и 9.43E-05
8.65E-05 8.65E-05 8.65E-05 8.65E-05 8.65E-05 8.65E-05 8.65E-05 8.65E-05 8.65E-05 8.65E-05 и 8.65E-05 и 8.65E-05 и 8.65E-05
7.91E-05 7.91E-05 7.91E-05 7.91E-05 7.91E-05 7.91E-05 7.91E-05 7.91E-05 7.91E-05 7.91E-05 В-05
7.21E-05 7.21E-05 7.21E-05 7.21E-05 7.21E-05 7.21E-05 7.21E-05 7.21E-05 7.21E-05 7.21E-05
6.55E-05 6.55E-05 6.55E-05 6.55E-05 6.55E-05 6.55E-05 6.55E-05 6.55E-05 6.55E-05 6.55E-05
5.93E-05 5.93E-05 5.93E-05 5.93E-05 5.93E-05 5.93E-05 5.93E-05 5.93E-05 5.93E-05 5.93E-05 В-05
5.34E-05 5.34E-05 5.34E-05 5.34E-05 5.34E-05 5.34E-05 5.34E-05 5.34E-05 5.34E-05 5.34E-05 В-05
4.79E-05 4.79E-05 4.79E-05 4.79E-05 4.79E-05 4.79E-05 4.79E-05 4.79E-05 4.79E-05
4.27E-05 4.27E-05 4.27E-05 4.27E-05 4.27E-05 4.27E-05 4.27E-05 4.27E-05 4.27E-05 4.27E-054.27E-05
Шаги
3.78E-05 3.78E-05 3.78E-05 3.78E-05 3.78E-05 3.78E-05 3.78E-05 3.78E-05 3.78E-05
3.33E-05 3.33E-05 3.33E-05 3.33E-05 3.33E-05 3.33E-05 3.33E-05 3.33E-05 3.33E-05 3.33E-05 и 3.33E-05 и 3.33E-05
2.91E-05 2.91E-05 2.91E-05 2.91E-05 2.91E-05 2.91E-05 2.91E-05 2.91E-05 2.91E-05 2.91E-05
2.51E-05 2.51E-05 2.51E-05 2.51E-05 2.51E-05 2.51E-05 2.51E-05 2.51E-05 2.51E-05 2.51E-05
2.15E-05 2.15E-05 2.15E-05 2.15E-05 2.15E-05 2.15E-05 2.15E-05 2.15E-05 2.15E-05 2.15E-05 Вр 2.15E-05 ВР2.15E-05
1.82E-05 1.82E-05 1.82E-05 1.82E-05 1.82E-05 1.82E-05 1.82E-05 1.82E-05 1.82E-05 1.82E-05
1.52E-05 1.52E-05 1.52E-05 1.52E-05 1.52E-05 1.52E-05 1.52E-05 1.52E-05 1.52E-05 1.52E-05 В-05
1.24E-05 1.24E-05 1.24E-05 1.24E-05 1.24E-05 1.24E-05 1.24E-05 1.24E-05 1.24E-05 1.24E-05
9.96E-06 9.96E-06 9.96E-06 9.96E-06 9.96E-06 9.96E-06 9.96E-06 9.96E-06 9.96E-06 9.96E-06
7.77E-06 7.77E-06 7.77E-06 7.77E-06 7.77E-06 7.77E-06 7.77E-06 7.77E-06 7.77E-06 7.77E-06 В-06
5.85E-06 5.85E-06 5.85E-06 5.85E-06 5.85E-06 5.85E-06 5.85E-06 5.85E-06 5.85E-06 5.85E-06
4.21E-06 4.21E-06 4.21E-06 4.21E-06 4.21E-06 4.21E-06 4.21E-06 4.21E-06 4.21E-06 4.21E-06 и 4.21E-06 и 4.21E-06 и 4.21E-06
2.84E-06 2.84E-06 2.84E-06 2.84E-06 2.84E-06 2.84E-06 2.84E-06 2.84E-06 2.84E-06 2.84E-06 В-06 2.84E-06 В-06
1.74E-06 1.74E-06 1.74E-06 1.74E-06 1.74E-06 1.74E-06 1.74E-06 1.74E-06 1.74E-06 1.74E-06 В-06
9.08E-07 9.08E-07 9.08E-07 9.08E-07 9.08E-07 9.08E-07 9.08E-07 9.08E-07 9.08E-07 9.08E-07 В-07
3.44E-07 3.44E-07 3.44E-07 3.44E-07 3.44E-07 3.44E-07 3.44E-07 3.44E-07 3.44E-07 3.44E-07 и 3.44E-07 и 3.44E-07 и 3.44E-07
56 C. Валидация
Таблица C.3. Количество итераций SQP за 10 запусков (при активном ограничении) .
Запускает
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
Шаги
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
57
Таблица C.4. Количество итераций метода активного набора за 10 запусков (при активном ограничении) .
Запускает
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
Шаги
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
Таблица C.5. Значения множителя Лагранжа λ 2 для 10 запусков (при активном ограничении) .
Запускает
0.1105 0.1105 0.1105 0.1105 0.1105 0.1105 0.1105 0.1105 0.1105 0.1105
0.9339 0.9339 0.9339 0.9339 0.9339 0.9339 0.9339 0.9339 0.9339 0.9339
0.8882 0.8882 0.8882 0.8882 0.8882 0.8882 0.8882 0.8882 0.8882 0.8882
0.8493 0.8493 0.8493 0.8493 0.8493 0.8493 0.8493 0.8493 0.8493 0.8493
0.8115 0.8115 0.8115 0.8115 0.8115 0.8115 0.8115 0.8115 0.8115 0.8115
0.7749 0.7749 0.7749 0.7749 0.7749 0.7749 0.7749 0.7749 0.7749 0.7749
0.7393 0.7393 0.7393 0.7393 0.7393 0.7393 0.7393 0.7393 0.7393 0.7393
0.7046 0.7046 0.7046 0.7046 0.7046 0.7046 0.7046 0.7046 0.7046 0.7046
0.6709 0.6709 0.6709 0.6709 0.6709 0.6709 0.6709 0.6709 0.6709 0.6709
0.6381 0.6381 0.6381 0.6381 0.6381 0.6381 0.6381 0.6381 0.6381 0.6381
0.6060 0.6060 0.6060 0.6060 0.6060 0.6060 0.6060 0.6060 0.6060 0.6060
0.5748 0.5748 0.5748 0.5748 0.5748 0.5748 0.5748 0.5748 0.5748 0.5748
0.5442 0.5442 0.5442 0.5442 0.5442 0.5442 0.5442 0.5442 0.5442 0.5442
0.5142 0.5142 0.5142 0.5142 0.5142 0.5142 0.5142 0.5142 0.5142 0.5142
0.4849 0.4849 0.4849 0.4849 0.4849 0.4849 0.4849 0.4849 0.4849 0.4849
0.4561 0.4561 0.4561 0.4561 0.4561 0.4561 0.4561 0.4561 0.4561 0.4561
Шаги
0.4278 0.4278 0.4278 0.4278 0.4278 0.4278 0.4278 0.4278 0.4278 0.4278
0.4000 0.4000 0.4000 0.4000 0.4000 0.4000 0.4000 0.4000 0.4000 0.4000
0.3727 0.3727 0.3727 0.3727 0.3727 0.3727 0.3727 0.3727 0.3727 0.3727
0.3457 0.3457 0.3457 0.3457 0.3457 0.3457 0.3457 0.3457 0.3457 0.3457
0.3191 0.3191 0.3191 0.3191 0.3191 0.3191 0.3191 0.3191 0.3191 0.3191
0.2928 0.2928 0.2928 0.2928 0.2928 0.2928 0.2928 0.2928 0.2928 0.2928
0.2667 0.2667 0.2667 0.2667 0.2667 0.2667 0.2667 0.2667 0.2667 0.2667
0.2409 0.2409 0.2409 0.2409 0.2409 0.2409 0.2409 0.2409 0.2409 0.2409
0.2154 0.2154 0.2154 0.2154 0.2154 0.2154 0.2154 0.2154 0.2154 0.2154
0.1900 0.1900 0.1900 0.1900 0.1900 0.1900 0.1900 0.1900 0.1900 0.1900
0.1648 0.1648 0.1648 0.1648 0.1648 0.1648 0.1648 0.1648 0.1648 0.1648
0.1397 0.1397 0.1397 0.1397 0.1397 0.1397 0.1397 0.1397 0.1397 0.1397
0.1147 0.1147 0.1147 0.1147 0.1147 0.1147 0.1147 0.1147 0.1147 0.1147
0.0897 0.0897 0.0897 0.0897 0.0897 0.0897 0.0897 0.0897 0.0897 0.0897
0.0648 0.0648 0.0648 0.0648 0.0648 0.0648 0.0648 0.0648 0.0648 0.0648
0.0399 0.0399 0.0399 0.0399 0.0399 0.0399 0.0399 0.0399 0.0399 0.0399
Международный журнал по твёрдым телам и структурам 43 (2006) 5658-5673
www.elsevier.com/locate/ijsolstr
Метод адаптивной плотности силы в задаче определения формы структур тенсегрити
Дж.Й. Чжан *, М. Осаки
Факультет архитектуры и архитектурной инженерии, Киотский университет, Киото-Дайгаку Кацура, Нисике, Киото 615-8540, Япония
Получено 9 мая 2005года; получено в пересмотренном виде 21 октября 2005года
Доступно онлайн 14 февраля 2006года
Дж.Я. Чжан, М. Осаки / Международный журнал по твердым телам и структурам 43 (2006) 5658-56735659
Автор- корреспондент . Тел.: +81 75 383 2903; факс: +81 75 383 2972.
Адрес электронной почты: is.zhang@archi.kyoto-u.ac.jp (Дж.Й. Чжан).
0020-7683/$ - см. переднюю тему - 2005 год, Изданный Elsevier Ltd.
doi: 10.1016/j.ijsolstr.2005.10.011
АННОТАЦИЯ
Представлен численный метод определения формы структур тенсегрити, в котором итеративно выполняются анализ собственных значений и спектральная декомпозиция для поиска решения по набору возможных плотностей силы, который удовлетворяет требованию недостатка ранга матрицы равновесия по отношению к узловым координатам. Показано, что матрице равновесия соответствует геометрическая матрица жёсткости в традиционной формулировке метода конечных элементов. При этом может быть получена новая невырожденная конфигурация структуры из независимого набора узловых координат. Даётся простое объяснение требованию недостатка ранга матрицы равновесия, что приводит к невырожденной структуре. Для иллюстрации надёжности и хорошей способности поиска новых конфигураций предлагаемого метода представлено несколько численных примеров .
2005 Издано Elsevier Ltd.
Ключевые слова: Структура Тенсегрити; Определение формы; Метод плотности силы; Спектральная декомпозиция
1. Введение
Натяжные конструкции - такие, как кабельные сети, мембранные конструкции и купола тенсегрити - обладают значительным преимуществом перед обычными стальнымиконструкциями ввиду их лёгкого веса. Поскольку натяжные конструкции могут передавать только осевые усилия, то распределение осевых сил напрямую связано со структурной формой, поэтому равновесная форма может быть определена с помощью так называемого анализа поиска формы, который одновременно находит возможный набор внутренних сил и геометрию конструкции.
Предложены некоторые различные определения и классификации структур натяжения, например, в некоторых исследованиях разработчики классифицируют их на (1) самонапряженные конструкции и (2) предварительно напряжённые конструкции. Самонапряжённые конструкции свободно стоят так, что могут поддерживать своё равновесное состояние без какой-либо поддержки извне. Предварительно напряжённые конструкции – такие, как купола тенсегрити, кабельные сети и мембранные конструкции - для получения равновесия требуют их крепления к опорам. В рамках данного исследования будем рассматривать метод плотности силы для предварительно напряжённых состояний структурных элементов как:(1) структуры тенсегрити и (2) растяжимые конструкции, которые состоят только из растяжимых элементов (elements).
Терминология тенсегрити, данная Фуллером (1975), относится к предварительно напряжённой структуре со штифтовым соединением, которая состоит из непрерывных растягиваемых элементов (тросов) и разрывных элементов сжатия (стоек). Однако, многие из так называемых структур тенсегрити, разработанных недавно на основе этой базовой идеи, не удовлетворяют этому определению строго. Более подробное описание и классификация структур тенсегрити были представлены Мотро (1996). В этом исследовании мы рассматриваем структуру тенсегрити как отдельно стоящую предварительно напряжённую систему кабель-распорка со штыревыми соединениями, где между распорками допускаются промежутки, например, в виде тросовых призм, предложенных Сайто и др. (2001) и Вангом (1996).
Процесс нахождения равновесной конфигурации, называемый поиском формы, является ключевым шагом в проектировании структуры тенсегрити. Многие исследователи внесли важный вклад в эту цель, например, Ханаор (1988), Пеллегрино и Калладайн (1986), Султан и др. (2002), Мотро и др. (1986). Возможности их методов поиска были расширены на основе идеи метода плотности силы, который первоначально был предложен для кабельных сетей Линквицем и Schek (1971) и считался очень эффективным, потому что в процесс поиска формы нужно решать только линейные уравнения. Среди них обнаружена аналитическая методика, разработанная Вассартом и Мотро (1999), которая может быть особенно подходящей для поиска новых конфигураций (Тиберт и Пеллегрино, 2003). Они проанализировали условия для плотностей силы в символической форме, чтобы матрица равновесия имела недостаток требуемого ранга. Однако, для структур с большим числом членов аналитический метод может быть недостаточно эффективным. В этом случае настоятельно рекомендуется использовать эффективные численные методы, что является темой этого исследования.
Статья организована следующим образом. В разделе 2 показана основная идея и формулировка метода плотности силы для задачи определения формы кабельных сетей и их расширения для структур тенсегрити, также просто представлено объяснение требования недостатка ранга матрицы равновесия. Раздел 3 объясняет линейную и геометрическую матрицы жёсткости и показывает, что матрица равновесия по отношению к узловым координатам эквивалентна матрице геометрической жёсткости. В разделе 4 формируется вектор плотности силы для условий матрицы равновесия с линейными ограничениями на плотности силы, что представляет собой адаптивную силу. Поиск формы основан на анализе собственных значений при спектральном разложении матрицы равновесия. Вразделе 5 приведено некоторое число реальных примеров, чтобы проиллюстрировать возможность и надёжность поиска новых конфигураций по предлагаемому методу. В завершающем разделе 6 обсуждаются полученные результаты.
2. Метод плотности силы
2.1. Свойства структур тенсегрити
Проблема определения формы структуры тенсегрити очень похожа на проблему кабельной сети, потому что они используют почти те же допущения, описанные следующим образом (за исключением пунктов (d) и (e), которые приняты только для структур тенсегрити):
(a) Элементы связаны штифтовыми соединениями.
(b) Известна связность между узлами и элементами, называемая топологией структуры, а метрическая конфигурация структуры описывается в терминах узловых координат.
(c) Не прилагается никакая внешняя нагрузка, а собственным весом конструкции пренебрегают, т.е. она находится в состоянии саморавновесия .
(d) Не учитывается деформация стоек (распорок) .
(e) Конструкция является отдельностоящей без какой-либо опоры.
Из предположений (a) и (c) следует, что взаимодействие между элементами описывается только осевыми силами (либо при сжатии, либо при растяжении).
Поскольку саморавновесное состояние кабельной сети должно быть получено путём рассмотрения взаимодействия между силами и геометрией, существуют некоторые трудности в процессе нахождения формы, поэтому было разработано несколько методов для их преодоления. Среди них метод плотности силы, который был первоначально разработан Линквиц и Шек (1971), считается одним из наиболее мощных подходов. Ключевая особенность метода плотности силы заключается в том, что нелинейные уравнения равновесия для неизвестных местоположений узлов имеют вид системы линейных уравнений относительно отношения внутренней силы элемента k к его длинее k qk = sk/lk,называемого плотностью силы элемента k. Обратите внимание, что qk > 0 для всех элементов кабельной сети, при этом кажется, что формулировка уравнений для кабельной сети может быть легко применена к задаче определения формы структур тенсегрити . Однако здесь есть некоторые трудности из-за того, что структуры тенсегрити являются отдельно стоящими, поэтому там существуют распорки с qk < 0.
2.2. Формулировка матрицы равновесия
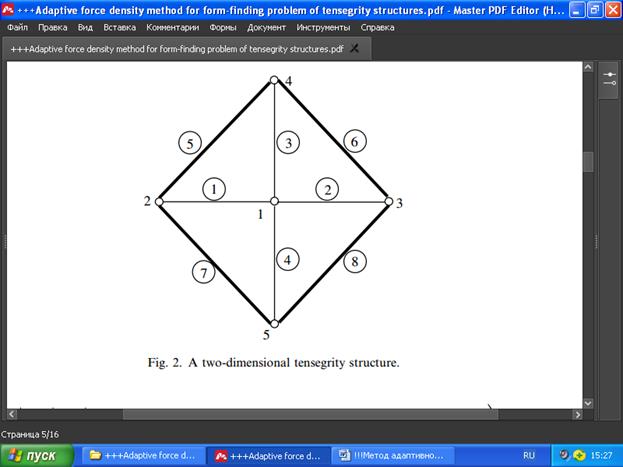
Начнём с основных формулировок метода плотности силы для кабельных сетей. Типичная кабельная сеть имеет узлы, прикреплённые к опорам и называемые фиксированными узлами, поскольку они не могут иметь никакого смещения. Тогда как узлы, которые не ограничены извне, называются свободными узлами. Например, двумерная кабельная сеть на Рис. 1 имеет два свободных узла 1 и 2 и прикреплена к неподвижным узлам 3-8. Структурные элементы, соединяющие узлы, называются элементами.
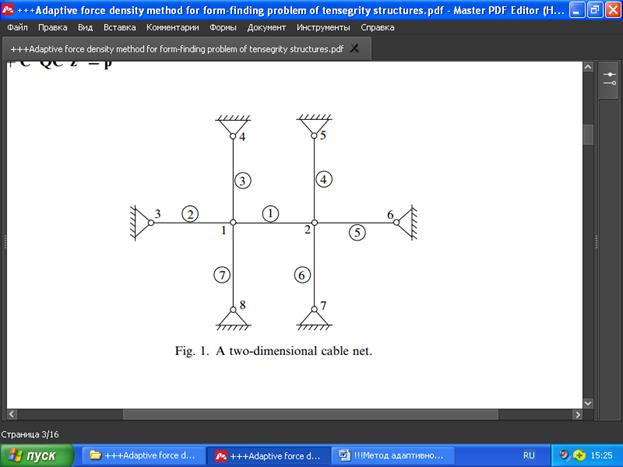
Рис. 1. Двумерная кабельная сеть.
f
Топология структуры из m элементов с n свободными узлами и nf фиксированными узлами описывается матрицей инцидентности Сs E Rm(n+nf) из теории графов (Кавех, 2004). Если элемент k выходит из узла i и входит в узел j (i < j), то i-й и j-й элементы k-й строки матрицы Cs устанавливаются равными 1 и -1 соответственно:
1 для p = i
s
Ck;p = −1 для p = j (1)
0 в остальных случаях
Для удобства в последовательной нумерации фиксированным узлам предшествуют свободные узлы так, что Cs разделена на две части:
s f
C = (C ; C), (2)
где C E Rmn и Cf E Rmnf описывают связи элементов со свободными и фиксированными узлами
соответственно.
Пусть x, y, z E Rn и x , y , z E Rnf обозначают векторы узловых координат свободных и фиксированных узлов соответственно. Вектор плотности сил элементов обозначим как q = (q1; q2; ...; qm)Т E Rm, тогда матрица плотности силы Q E Rmm задаётся в виде диагонали значений
Q = diag(q) (3)
Уравнения равновесия свободных узлов в каждом направлении x,y,z общей конструкции со штыревыми соединениями можно записать следующим образом (Линквиц и Шек, 1971; Schek, 1974):
CТQCx + CТQCfxf = Px
CТQCy + CТQCfyf = Py (4)
CТQCz + CТQCfzf = Pz
где Px, Py и Pz являются проекциями внешних нагрузок, приложенных к свободным узлам в направлениях x, y и z соответственно.
Исходя из матричной структуры уравнений, для упрощения вычислений определяются матрицы E E Rnn и Ef ERnnf
E = CТQC (5)
Ef =CТQCf
Эти матрицы являются постоянными, когда заданы плотности сил. Исходя из (4) и (5), систему уравнений саморавновесия без внешних нагрузок окончательно запишем в виде:
Ex = −Efxf
Ey = −Efyf (6)
Ez = −Efzf
Эти уравнения являются линейными по отношению к неизвестным координатам x, y и z свободных узлов при заданных координатах x f, y f, zf фиксированных узлов. Поскольку матрица E описывает равновесие свободных узлов, она называется в этом исследовании матрицей равновесия.
Вместо того, чтобы использовать (5) с матрицами C и Q , можно записать E непосредственно из плотностей силы q (Коннелли и Террелл, 1995; Вассарт и Мотро, 1999). Пусть I обозначает множество элементов, подключенных к свободному узлу i, тогда значения E(i,j) матрицы E будут равны:
k∑qk для i = j
Е = −qk, если свободные узлы i и j соединены элементом k (7)
0 в других случаях
Например, для плоской (двумерной) кабельной сети на рис. 1 матрица E может быть записана непосредственно из (7):
q1 + q2 + q3 + q7 −q1
E =
−q1 q1 + q4 + q5 + q6
То есть E - всегда квадратная и симметричная матрица, более того, она положительно определённая, т.е. все её члены находятся в напряжении qk >0(k =1,2,...,m) без изолированных свободных узлов (Schek, 1974). Следовательно, E обратима, поэтому координаты свободных узлов могут быть однозначно определены решением системы линейных уравнений (6) - это и есть оригинальная идея метода плотности силы для задачи определения формы кабельных сетей.
2.3. Метод определения плотности силы для структур тенсегрити.
Формулировка, аналогичная методу плотности сил для кабельных сетей, может быть применена к структурам тенсегрити, поскольку для них используются почти те же допущения, что перечислены выше в разделе 2.1. Однако, для структур тенсегрити матрица равновесия E всегда имеет недостаток ранга и поэтому необратима, потому что они являются автономными и поэтому обязательно имеют сжимаемые элементы (распорки, стойки) qk <0 (см.выше). Поскольку в структурах тенсегрити также не существует фиксированных узлов, уравнения саморавновесия без узловых нагрузок в каждом направлении x,y,z имеют простой вид однородной системы:
Ex = 0
Ey = 0 (8)
Ez = 0