Рисунок 1. 3. Полностью собранный прототип робота superball, разработанный в dtrl, nasa (и сточник: [48] с согласия автора).
Кроме того, благодаря податливым свойствам своего тела структуры тенсегрити открывают возможности их применения во взаимодействии с человеком [31]. Ведь современные роботы – это чаще всего тяжёловесные, жёсткие и мощные конструкции, что делает такое взаимодействие опасным. Также возможной областью их применения является достижение областей, недоступных или опасных для человека, что было исследовано, например, при лазании в труднодоступных местах при осмотре воздуховодов [13, 14].
При проектировании робота необходимо учитывать несколько факторов, начиная с
механического дизайна до управления стратегиями. Например, ключевым компонентом в любой сборке робота являются приводы, и роботы тенсегрити не являются здесь исключением: в сборках тенсегрити могут использоваться различные приводы, найденные в литературе - например, сплавы с памятью формы [41, 50], пневматические искусственные мышцы [9, 32], скрученные полимерные мышцы (TCPM) [21, 59] и линейные двигатели постоянного тока [30]. Все эти приводы имеют ограничения, которые должны быть учитываться при постройке робота и управлении им (например, ограничения на ход, на крутящий момент и на скорость). Конкретный практический пример ограничений TCPM можно найти в Приложении B.
1.2. Управление структурами тенсегрити
Первоначально стратегии управления тенсегрити представляли собой классические схемы управления с разомкнутым контуром [1, 37], но с учётом сложности конструкций вскоре робототехника начала склоняться к использованию искусственного интеллекта. В 2013 году Искен с соавт. [26] сравнили два разных метода машинного обучения: подходы к управлению с ручным кодированием, одноагентное и мультиагентное обучение. Было исследовано управление с помощью центральных генераторов паттернов (CPG) для пловца-тенсегрити [3] и на роботах Tetraspine & ReCTeR [7, 55], показавших при моделировании многообещающие результаты.
Другой областью управления роботами-тенсегрити является использование вибрационных приводов. Хазанов и др. [28, 29] объединили морфологическое вычисление с действием вибрации, чтобы использовать сложность тенсегрити для передвижения робота [4]. Напротив, Бем. [4] исследовал передвижение с помощью одного вибрационного привода, чтобы упростить все элементы управления. Робот ReCTeR был протестирован с использованием различных стратегий управления, таких, как коэволюционный контроль, биоинспирированный контроль и контоль физического пространства [7].
Коэволюция с разомкнутым контуром как традиционное управление было адаптировано из предыдущей работы Панайта [42] к икосаэдрическим роботам тенсегрити (Искен и другие [25]). Было продемонстрировано, что элементы управления машинным обучением могут обеспечить надёжное катящееся передвижение икосаэдрических роботов без понимания их аналитической динамики.
Биоинспирированный подход к управлению разделён на три различных метода:
реактивное управление, управление инверсной кинематикой и управление на основе CPG. Все они являются управлениями с замкнутым контуром и имели один и тот же основополагающий принцип, согласно которому скорость и направление движения робота контролировались смещением его центра масс.
Сферический робот-тенсегрити, разработанный Бемом и др., был протестирован с использованием замкнутого (циклического) управления. В принципе, этот метод смещает центр масс робота (ЦМ) за пределами площади опоры через внутреннее движение масс, чем достигается опрокидывание и при последовательном применении - подвижность по перекатыванию. Площадь опоры (ПО) определяется каждой точкой соприкосновения.с землёй, которые объект создаёт своей опорной поверхностью. Кроме того, для устойчивости в передвижении объект должен ограничивать свой ЦМ внутри ПО так, что хотя бы в положении стоя структура остаётся в равновесии [11, 34, 43]. Это может быть важно при передвижении структур тенсегрити, когда, например, перемещающийся по икосаэдру робот-тенсегрити катится, смещая свой центр массы за пределы своего основания, что приводит к появлению нового опорного треугольника, т.е. трёх контактных узлов, определяющих новую площадь опоры. Путём упорядочивания этих операций может быть реализован управляемый способ передвижения робота.
.
Коидзуми, Хираи и Сибата (2012-13) [22, 32] использовали предложенный ими в 2009 году принцип [50], чтобы продемонстрировать использование разомкнутого контура в управлении их роботом-икосаэдром. Их принцип управления гласит, что гравитационная потенциальная энергия роботизированной системы минимальна при естественном устойчивом состоянии. При приведении в действие мышц конструкции происходит нелинейное распределение силы, в результате чего изгибающий момент вокруг основания контакта робота с землей вызывает переход от одного контактного треугольника к другому. То есть здесь используется тот же принцип, что и упомянутый выше, однако, из-за сложности такой динамики робота авторы не пытались аналитически предсказать, какие мышцы должны работать в каждый момент времени для целенаправленного передвижения. Ким и др. в 2014 году [30] использовали аналогичный принцип разомкнутого контура в наборе для быстрого прототипирования икосаэдрических роботов-тенсегрити. Ву и др. (2016) [59] также продемонстрировали разомкнутый (без обратной связи) контур управления своим роботом-икосаэдром, аналогично Коидзуми и др., но их фокус внимания был больше сосредоточен на приведении в действие мышц из скрученного и намотанного полимера, чем на моделировании контактов.
Робот-альпинист DuCTT (v1-2) передвигался подъёмом с использоваением метода плотности сил через управление инверсной кинематикой [13, 14]. Эта стратегия управления с разомкнутым контуром (без обратной связи) показала многообещающие результаты и построена на тех же принципах, что и описанный в следующем разделе планировщик всего тела.
.
1.3. Полный Эталонный План тела
В 2017 году Гидо Турнуа предложил стратегию эталонного планирования приводов, способную обеспечить передвижение тенсегрити-роботов через более контролируемые движения всего тела [56]. Он назвал свой метод Полным Справочным Планом Тела (FBRP). Эта стратегия представляет собой числовой эталонный планировщик, который определяет последовательность равновесных конфигураций для данной задачи. Во-первых, здесь уравнения статического равновесия получаются по методу плотности сил, что в сочетании с кинематическим методом деформаций определяет систему уравнений равновесного управления [44].
Хотя FBRP является эффективным методом поиска последовательности равновесных конфигураций для передвижения структуры тенсегрити по требуемой траектории в пространстве, однако, он может быть дополнен условиями-ограничениями в виде неравенств. Как уже упоминалось, он может эффективно учитывать ограничения в виде равенств, а попытки использования неравенств терпят здесь неудачу, поскольку они не являются дифференцируемыми. Это создаёт проблему при работе с определёнными ограничениями, например, для привода и при расчётах на устойчивость.
1.4. Цель работы
Цель этого дипломного проекта заключается в нахождении и внедрении надёжного способа учёта ограничений в виде неравенств при управлении структурами тенсегрити с использованием FBRP. Это делается с помощью дополненного метода последовательного квадратичного программирования при обеспечении ограничений в виде неравенств. Такая расширенная реализация делает FBRP более осуществимым на практике. Наконец, этот подход был окончательно подтверждён различными практическими приложениями, например, при ограниченных изменениях силы растяжения тросов и расположении центра масс в заданном пространстве, что гарантирует соблюдение физических ограничений для исполнительных механизмов. Кроме того, ограничения на положение ЦМ структуры способствуют достижению устойчивости, что делается путём ограничения площади опоры при отслеживании траектории.
2. Полный Эталонный План тела - справочная информация.
В этой главе описывается метод FBRP для отслеживания траектории структур тенсегрити, предложенный Guido Турнуа в 2017 году [56]. Входные данные FBRP представляют собой желаемый набор состояний тенсегрити, а именно, траекторию в координатах узлов. Затем планировщик отображает изменение состояния (переменных) при достижении набора равновесных конфигураций с отслеживанием желаемой траектории. Здесь и далее используются следующие допущения:
- Тросы не имеют массы;
- Стержни считаются бесконечно жёсткими по отношению к тросам;
- Игнорируется влияние толщины стержня;
- Квазистатическое поведение, т.е. скорости и ускорения равны нулю;
- Силы действуют только на узлы элементов;
- Внешними силами, отличными от гравитационной силы, и их реакциями пренебрегают;
- Силы растяжения считаются положительными, а силы сжатия - отрицательными;
2.1. Уравнения равновесных сил
Структура тенсегрити моделируется в виде точек в пространстве, обозначающих положения узлов. Узлы соединяются жёсткими сжатыми элементами, обозначаемыми как стержни, и гибкими растянутыми элементами, обозначаемыми как тросы. Зададим декартову систему координат x, y, z, в которой будем моделировать структуру тенсегрити с N узлами и M элементами (стержнями и тросами). Координаты i-го узла обозначим как x i , y i ,z i, действующие на узел i проекции внешних сил – как F i,x ext , F i,y ext и F i,z ext . В теории плотности сил [12] показано, что уравнения силового равновесия для узла i могут быть записаны в виде:
∑(x j − x i )q i,j + F i,x ext = 0 (2.1a)
∑(y j − y i )q i,j + F i,y ext = 0 (2.1a)
∑(z j − z i )q i,j + F i,z ext = 0 (2.1a)
где в соответствии с методами поиском формы структур тенсегрити [12, 57, 61, 62] q i,j = f i,j /l i,j - плотность силы f i,j элемента длиной l i,j, соединяющего узел i с узлом j .
Определим матрицу инцидентности C ≈ 2RM×N [62] для упрощения системы 3N уравнений равновесия, содержащую информацию о подключениях элементов к узлам:
1 для p = i
Ck,p = −1 для p = j (2.2)
0 в других случаях
где k обозначает номер строки матрицы с информацией о соединениях k-го элемента
с двумя узлами.
Обозначим набор векторов узловых координат в декартовой системе для N узлов как
x = (x1,x2,...,x N )Т ∈ RN (2.3a)
y = (y1, y2,..., y N )Т ∈ RN (2.3b)
z = (z1,z2,...,z N )Т ∈ RN . (2.3c)
Кроме того, определим вектор плотности сил M элементов как q = (q1,q2,...,q M) ∈ RM [12, 57, 61, 62]. Тогда уравнения равновесия для N узлов (2.1) можно записать в виде [54, 62]:
CТQCx + Fx ext= 0 (2,4а)
CТQCy + Fy ext= 0 (2.4b)
CТQCz + Fz ext = 0 (2,4°c)
где Q - диагональная матрица плотности силы с элементами вектора q по диагонали и Fx ext , Fy ext и Fz ext являются внешними силами, действующими на каждый узел в соответствующих направалениях.
2.2. Планировщик ссылок
Конфигурация структуры тенсегрити описывается набором внутренних состояний, представленных узловыми координатами и векторами плотности сил. Поэтому определим вектор ξ для совместного представления формы и степеней свободы структуры тенсегрити:
ξ = (xТ, yТ, zТ, qТ )Т .
Тогда можно переписать систему (2.4) как нелинейную функцию f : R3N+M→ R3N от ξ:
f (ξ) = 0 (2.5)
Как указывалось в ранее перечисленных предположениях, мы считаем здесь F x ext = F y ext = 0 и предполагаем, что тросы не имеют массы. В направлении z учтены гравитационные силы и силы реакции грунта (GRF), при этом предполагается равномерное распределение массы стержней, чтобы гравитация была равнораспределённой между двумя узлами на каждом стержне, тогда:
F i,z ext = F j,z ext = mrg/2 (2.6)
где mr - масса стержня и g – ускорение свободного падения.
GRF моделируются таким образом, что они поддерживают весь вес структуры, при этом уравнения равновесия контактного узла nc суммируются и приравниваются отрицательной гравитационной силе:
∑f nc = −mrg (2.7)
Пусть (g1 (ξ) = 0, ... , g h (ξ) = 0) - h непрерывных уравнений ограничений в виде равенств. Тогда общая матрица системы J : R3N+M→ R3N+h может быть определён в виде:
f (ξ)
g 1(ξ)
J(ξ) = … =0 (2.8)
g h (ξ)
Если конфигурация удовлетворяет условию J(ξ) = 0, структура тенсегрити находится в состоянии равновесия. Следовательно, J преобразует конфигурационное пространство структуры в неявно определённое многообразие при равновесии.
Чтобы отслеживать искомые траектории узлов, нужно определить S точек равновесия структуры на этом пути. Пусть ξc обозначает множество контролируемых переменных состояния с подмножеством искомых узловых координат ξc,d. Далее разделим переменные состояния на определяемые и свободные ξ = (ξcТ ,ξfТ )Т , где последние не ограничены отслеживаемыми траекториями. Чтобы выполнялось предположение о квазистатическом поведении, J должно быть всё время равно нулю, в том числе при смене равновесных конфигураций. Состояния тенсегрити имеют линейную зависимость своей скорости, поскольку J является системой второго порядка [45], при этом изменение J аппроксимируется производной первого порядка по ξ, умноженной на дискретное изменение состояния конфигурации:
∆J ≈ δJ/δξ *∆ξ = 0, (2.9)
где δJ/δξ - матрица Якоби. Учитывая, что ∆ξ достаточно мало, это соотношение можно использовать для оценки изменений состояния, необходимых для перемещения по узловой траектории, пребывая на ограниченном равновесном многообразии. Состояния ξc,d искомой траектории дискретизируются на S +1 шагах для достижения S желаемых изменений состояния.
Обратите внимание, что при использовании этого метода в J не могут быть включены ограничения в виде неравенств, поскольку они не дифференцируемы. Потому далее мы преобразуем уравнение (2.9) отдельно относительно определяемых и свободных переменных состояния:
∆J = δJ/δξc *∆ξc,d + δJ/δξ f *∆ξ f = 0, (2.10)
что позволит нам связать изменения отслеживаемых (искомых) переменных с изменением свободных переменных:
δJ/δξ f *∆ξ f = − δJ/δξc*∆ξc,d (2.11)
Матрицы Якоби δJ/ δξf и δJ/δξc имеют дефицит ранга по столбцам и поэтому являются сингулярными, что означает недоопределение этих уравнений с бесконечным числом их решений. Обращение матриц даёт решение в виде:
∆ξ f = (δJ/δξ f)Т(−δJ/δξc*∆ξc,d) (2.12)
Отсюда можно определить изменение всех переменных состояния на основе конфигурации ξ s для обеспечения последовательности равновесных конфигураций:
ξs+1 = ξs + ∆ξc,d (s→s+1) (2.13)
∆ξ f (s→s+1)
Поскольку изменение состояния определяется приближением первого порядка, неизбежны численные ошибки, которые могут привести к неправильному определению якобиана и соответственно к получению очень неточного приближения ξs+1. Для уменьшения этих численных ошибок псевдоинверсия может быть выполнена с разложением по сингулярным значениям, где единичные значения ниже установленного допуска устанавливаются равными нулю [19].
2.3. Начальные условия
Чтобы использовать эталонный планировщик, прежде должна быть определена начальная равновесная конфигурация ξ0. Эта конфигурация может быть определена с помощью следующей задачи оптимизации :
min { f (ξ), ││ξd − ξ││ } (2.14a)
ξ
при условиях g (ξ) = 0 (2.14b)
ξlb ≤ ξ ≤ ξub (2,14c)
где ξd - множество желаемых состояний, g (ξ) - ограничения, а ξlb и ξub – границы узловых координат и плотностей сил.
3. Методика
В этой главе описана методика полного управления структурой тенсегрити при определении набора ограничений в виде неравенств. Управление структурой здесь по-прежнему осуществляется эталонным планировщиком, который вычисляет последовательность равновесных конфигураций для получения желаемой траектории, то есть методика основана на теории плотности сил [12] и методах поиске формы структур тенсегрити [12, 57, 61, 62]. Однако, из-за особенностей этого метода он не может включать неравенства напрямую, поэтому планировщик был расширен, чтобы включить в решения, описанные ранее, ограничения в виде неравенств для практических приложений. Это достигается посредством последовательного квадратичного программирования, основанного на теориях Джилла и Мюррея (1978) [16], Шмида и Биглера (1994) [49] и Нокедала и Райта (2006) [39]. При этом итеративно удовлетворяются условия Каруша-Куна-Таккера (KKT) квадратичной программы [33], а затем используется метод линейного поиска для коррекции второго порядка. Каждый шаг делается с помощью метода активного набора [16, 18, 49]. В остальном метод основывается на предположениях, перечисленных в главе 2.
3.1. Добавление ограничений в виде неравенств
В этом разделе рассматривается метод включения ограничивающих внеравенств в базовый план. Как указывалось ранее, ограничения в виде неравенства не являются дифференцируемыми и, следовательно, не могут быть напрямую добавлены в уравнение (2.8).
Система уравнений (2.12) является недоопределённой детерминированной системой с бесконечным числом решений. Для удобства перепишем её в виде:
d = AТr (3.1)
где d = ∆ξf, A = (δJ/δξf) и r = (- ΔJ /δξc*∆ξc,d). В соответствии с обобщённой обратной теорией [27], если линейная система уравнений имеет какие-либо решения, то все они могут быть представлены в виде:
d = AТr + (I − AТA )w, (3.2)
где I - единичная матрица, а w - произвольный вектор. Решение (решения) существует тогда и только тогда, когда AAТr = r . А если решение существует, оно единственно тогда и только тогда, когда A имеет полный ранг по столбцам, и в таком случае I − AТA является нулевой матрицей. В нашем случае A имеет недостаток ранга по столбцам, поэтому система (3.1) недоопределна, как уже упоминалось ранее. Следовательно, всё возможное (бесконечное) число решений задаётся уравнением (3.2). Для удобства обозначим M = I − AТA, тогда уравнения (3.2) перепишутся в виде:
d = AТr + Mw (3.3)
Теперь мы можем задавать произвольный вектор w для получения решения, удовлетворяющего определённым критериям. Вектор w можно определить итеративным способом посредством минимизации dТd, что даёт свободу использования недифференцируемых ограничений в виде неравенств. Таким образом, определена задача оптимизации:
min (AТr + Mw)Т (AТr + Mw) (3.4а)
w
при условиях c i ≥ 0 (3.4b)
где c i могут быть n ограничениями в виде неравенств, где {n ∈ Z : n ≥ 0}. Отбрасывание выражений без w и расширение целевой функции приводит к схеме оптимизации:
min f(w) = wТMТMw + 2wТMТAТr (3.5а)
w
при условиях. c i (w) ≥ 0 (3.5b)
Теперь это задача квадратичного программирования (QP), которую можно решить с помощью этой схемы оптимизации. С помощью этого метода теперь мы можем получить набор равновесных конфигураций для получения желаемой траектории перемещения при соблюдении ограничений в виде неравенств. При этом обеспечивается также возможность принудительного задания различных ограничений, например, для привода и для повышения устойчивости.
Чтобы решить эту задачу, мы используем надёжный метод последовательного квадратичного программирования (SQP).
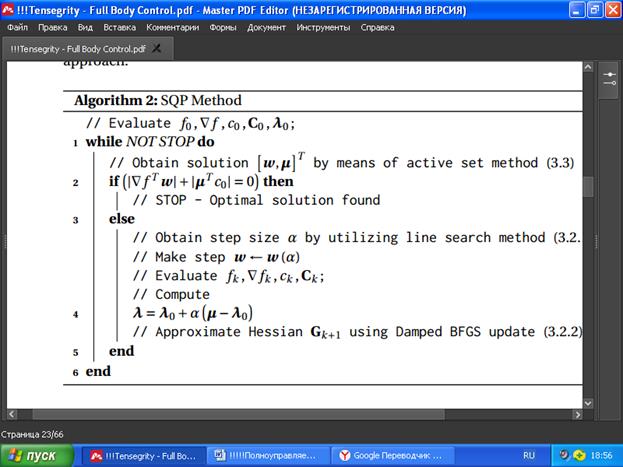
3.2. Последовательное квадратичное программирование
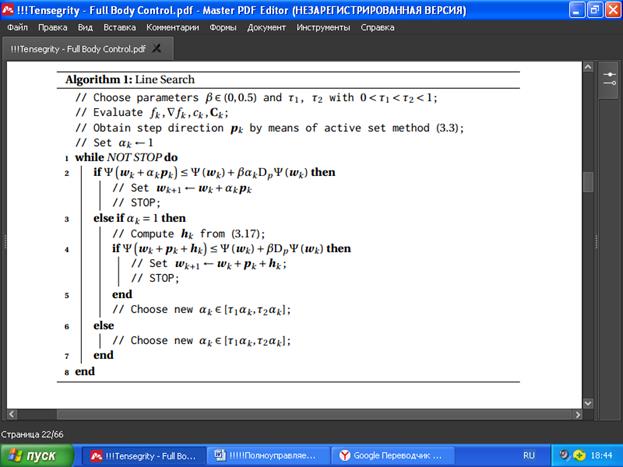
Последовательное квадратичное программирование является эффективным методом решения задач оптимизации .при использовании нелинейных ограничений. Он основан на принципе итеративного решения квадратичной программной подзадачи до тех пор, пока не будет реализована оптимальность. В этой реализации QP подзадача решается на каждой итерации с помощью метода активного набора (множества), определённого в разделе 3.3. Затем это решение корректируется с использованием метода линейного поиска для повышения надёжности и эффективности [58]. Этот подход можно рассматривать как обобщённую версию метода Ньютона.
Шаг Ньютона для функции g на шаге k определяется как
g (x k) + ∇g(x k)Т∆x = 0 . (3.6)
В этом случае функция g будет соответствовать условиям KKT для данной функции Лагранжа. Определим функцию Лагранжа для нашей задачи (3.5):
L (w,λ) = f (w) − λТc(w), (3.7)
где λ - вектор множителей Лагранжа. Оптимальность достигается путём решения задачи, соответствующей условиям KKT, которые определяются в матричной форме:
K(w,λ) = ∇w L (w,λ) = ∇f(w)−∇c(w) λ (3.8)
∇λ L (w,λ) −c(w)
Соответствующий градиент равен
∇K(w,λ) = ∇2ww L (w,λ) −∇c(w) (3.9)
−∇c (w)T 0
где ∇2ww L (w,λ) = ∇2f(w) − ∑λ i ∇2c i (w) . (3.10)
В итоге мы можем записать шаг Ньютона в виде:
(∇2ww L (w,λ) −∇c(w) ) (w) = ∇f(w) − ∇c(w) λ (3.11)
( −∇c(w)Т 0 ) (∆λ) −c (w)
и соответствующую квадратичную программу:
min 1/2wT∇2ww L (w,λ)w + ∇w L (w,λ)T w (3.12a)
w
при условии ∇c(w)T w ≥ −c (w) (3.12b)
Согласно Gill and Wong (2012) [17], теперь мы можем упростить систему KKT, представив ∆λ = µ − λ:
∇2ww L (w,λ) −∇c(w) ( w ) =∇f(w) (3.13)
∇c(w)T 0 ( µ ) −c(w)
Эта упрощённая система соответствует итоговой квадратичной программе, которая решается на каждой итерации с использованием метода активного набора:
min 1/2wT∇2ww L (w,λ)w + ∇f (w)T w (3.14a)
w
при условии ∇c(w)T w ≥ − c(w) (3.14b)
3.2.1. Линейный поиск
Определим оценочную функцию Ψ и рассмотрим шаг wk + α kpk, используя поправку α k в
направлении шага pk:
Ψ (wk+ α kpk, µ) = f (wk+ α kpk )+ ∑ µ i c i (wk+α kpk ) (3.15)
Вычислим производную по направлению DpΨ в направлении p k :
DpΨ(wk, µ ) = ∇f T pk − ∑µ i c i (wk+α kpk ) . (3.16)
Теперь мы можем определить шаг коррекции второго порядка:
hk = −Ck T( CkCk T )-1c (wk+pk ) (3.17)
где C = ∇c (w).
Итерационная процедура определена в Алгоритме 1:
3.2.2. Приближение Гессе.
Гессиан лагранжиана ∇2ww L (w,λ) является вычислительно дорогостоящим при получении и поэтому используется его приближение. Оценка гессиана Gk лагранжиана может быть получена на основе условия секущей:
s = wk+1− wk (3.18)
y = ∇L(w k+1,λk+1) − ∇L(w k,λk+1) (3.19)
Gk+1 = Gk + ууT / уTs − GkssTGk / sTGk s (3.20)
Если Gk положительно определена и yTs > 0, то Gk+1 будет положительно определённой. Заменив y по формуле обновления BFGS, мы используем обновление Powell-SQP (затухающее обновление BFGS) [46] с оценкой
yˆ = θy + (1 − θ)Gks , θ ∈ [0,1] , (3.21)
которая обеспечивает выполнение yTs > 0 и, следовательно, положительную определённость аппроксимированного гессиана.
3.2.3. Алгоритм последовательного квадратичного программирования
Алгоритм 2 определяет метод последовательного квадратичного программирования в терминах итеративного процесса:
3.3. Метод активного набора
В этом разделе подробно описывается метод активного набора, используемый для решения QP на каждой итерации способ SQP. Метод активного набора основан на теории [16, 18, 39, 49].
3.3.1. Предопределение
Соответствующий QP определяется как:
min f (w) = 1/2wTGw + aTw (3.22a)
w
при условии s i (w) = c i T (w ) − b i ≥ 0, i ∈ N (3.22b)
где G - наше приближение Гессе и a = ∇f (w). Далее определяем функцию Лагранжа:
L (w,µ) = 1/2wTGw + aTw − ∑µ i ( c i Tw − b i ) (3.23)
Тогда сответствующая задача максимизации, или двойная программа определится как
max L(w,µ) = 1/2wTGw + aTw − ∑ µ i ( c i Tw − b i ) (3,24а)
w,µ
при условиях Gw + a − ∑µ i c i = 0 (3.24b)
µ i ≥ 0, i ∈ N (3.24c)
Условия Каруша-Куна-Такера в двойной программе (3.24) могут быть определены как
Gw* + a − ∑µ i * c i = 0 (3,25а)
s i (w*) =c i T w* − b i = 0, i ∈ A(w*) (3.25b)
s i (w*) = c i Tw* − b i ≥ 0, i ∈ N\ A(w*) (3,25°c)
µ i ≥ 0, i ∈ N∩A(w*) (3.25d)
Ключевым элементом метода активного набора является отслеживание рабочего набора A, ограничения которого в этом наборе удовлетворяют следующим условиям:
Gw + a − ∑µ i c i = 0 (3,26а)
s i (w) = c i Tw − b i = 0, i ∈ A(w) (3.26b)
µ i ≥ 0, i ∈ A(w) . (3.26c)
Множители Лагранжа, соответствующие ограничениям, которых нет в текущем рабочем наборе, определяются как ноль.
Таким образом, основу метода можно кратко резюмировать следующим образом. Он реализуется в три этапа.
На этапе 0 мы определяем начальное предположение w0 , как показано в разделе 3.3.2.
На этапе 1 мы проверяем, нарушались ли какие-нибудь заданные ограничения - если таковых нарушенных нет, наше решение выполнимо и оптимально. Если же есть какие-либо нарушенные ограничения, мы выбираем одно из них и продолжаем…
На этапе 2 вычисляется новое решение посредством определения направления шага (раздел 3.3.3) и длины шага (раздел 3.3.4). На этом этапе мы определяем, какую длину шага следует использовать и надо ли удалить или можно добавить ограничения к рабочему набору, при этом сохраняя реализуемость (раздел 3.3.5,).
Фазы 1 и 2 повторяются до тех пор, пока не будет достигнуто оптимальное решение.
3.3.2. Первоначальное предположение
Чтобы задании начального предположения в методе активного множества мы начинаем с установки пустого множества и задания всех множителей Лагранжа равными нулю:
A =Ø (3.27)
µ i = 0 .(3.28)
Тогда легко определить разумное исходное предположение из решения уравнений:
w0 = −G-1a (3.29)
представляющих собой неограниченную систему KKT (3.25a).
3.3.3. Направление шага
Если на итерации n не получено оптимальное решение, то нарушается ограничение s r. Чтобы удовлетворить нарушенному ограничению, нужно сделать шаг, сохраняя при этом выполнимость решения.
£ ¤Т
Цель состоит в том, чтобы получить пошаговое направление p,v путем решения системы уравнений на основе матрицы форма - это делается с помощью метода нулевого пространства, описанного в Приложении A. Кроме того, в этой части мы предполагаем следующее:
£ ¤
• C = c i имеет полный ранг столбца
я∈А
• G симметрично и положительно определено
£ ¤
• µ = µ i
я∈А
• c r - нарушенное ограничение, а µ r - соответствующий множитель Лагранжа
Определим новый шаг:
w¯ = w + z = w + tp (3.30a)
i = µ i + u i = µ i + t v i i ∈ A (3.30b)
r = r + t , (3,30°c)
где t - длина шага и
· ¸ · ¸
z п
= t . (3.31)
u в
Запишем (3.24b) и (3.26b) в матричной форме:
G −C w a c r
T + − µ r = 0 , (3.32)
−C 0 µ b 0
и расширяться:
· ¸· ¸ · ¸ · ¸ · ¸· ¸ · ¸
G −C w a c r G −C z c r
T + − µ r + T − t = 0 . (3.33)
−C 0 µ b 0 −C 0 u 0
Согласно условиям из (3.24b) и (3.26b), уравнение (3.33) сводится к следующему:
G −C z c r
T − t = 0 . (3.34)
−C 0 u 0
Затем мы подставляем (3.31) и получаем желаемую систему:
G −C p c r
T = . (3.35)
−C 0 v 0
3.3.4. Длина шага
Здесь описывается нахождение длины шага t. Сначала определим, что мы называем частичной длиной шага t1
µ ¶
−μ i
t1 = min ∞, min ≥ 0 , (3.36)
i;v i<0 v i
что является максимальным шагом в двойственном пространстве без нарушения двойной осуществимости. Далее нам нужно чтобы посмотреть на полную длину шага t2 , которая является минимальным шагом в первичном пространстве, таким, что vio-установленное ограничение s r становится выполнимым. Чтобы получить t2 , нам нужно посмотреть на влияние на двойственный программа. Сосредоточив внимание только на нашем нарушенном ограничении, давайте рассмотрим лагранжиан при w ,µ
¡ ¢ ¡ ¢ 1
2 Т
L w ,µ − L w,µ = − t c r p − t s r (w) . (3.37)
2
Далее мы определяем наибольшее приращение двойной программы по отношению к t
дЛ Т
= −tc r p − s r (w) . (3.38)
dт
Исходя из этого, можно найти полную длину шага t2
−s r (w)
t2 = . (3.39)
T
c r п
T
Наконец, в случае c r p =6 0, тогда длина шага t, выбранная как минимальная из двух t1 и t2, равна:
t = min(t1,t2) . (3.40)
3.3.5. Добавление и удаление ограничений
В этом разделе мы рассмотрим, когда следует добавлять и удалять ограничения из рабочего набора A . Было показано, что решить систему (3.35) можно только в том случае, если выполняется следующее:
- G является положительно определенной,
- C имеет полный ранг по столбцам.
Установим, когда ограничение должно быть удалено из рабочего набора A , т.е. когда второе условие не выполняется. Это происходит, когда ограничения в C = [c i ]i∈A и c r являются линейно зависимыми. Это создает проблему при отслеживании рабочего набора, поэтому к C необходимо добавить ограничение c r. С этим можно справиться, отбросив ограничение j из A, чтобы сохранить полный ранг столбца C после добавления c r . Когда ограничение должно быть отброшено, мы идентифицируем его и получаем его индекс j с помощью
−μ дж
j = argmin . (3.41)
j;v j<0 v j
Теперь посмотрим, когда ограничение добавляется к рабочему набору A . Это происходит, когда шаг w¡,µ → w¡ ,µ неосуществим, т.е. c r T p =6 0. В случае, если это произойдет, мы добавим индекс rк¡¢ A и сделаем максимально возможный шаг t в двойственном пространстве от w,µ до указанного ограничения c r блокирует нас.
3.3.6. Алгоритм метода активного набора
Алгоритм 3 определяет метод активного набора как следующий итеративный процесс:
Алгоритм 3: Метод активного набора
−1
// Получить начальное предположение спомощью неограниченного минимума w0 = −Ga. Установить
A = ;, µ i = 0.
1 пока НЕ ПЕРЕСТАНУ делать
2 если s i (w) ≥ 0, i ∈ N ,то
// СТОП -Найдено оптимальное решение
3 еще
// Выберите нарушенное ограничение s r (w) < 0
4 конец
5 пока s r (w) < 0 ,выполните
£ ¤Т
// Определить направление шагаp,,,v
T
6 если c r p = 0 ,то
7 если v i ≥ 0, i ∈ A ,то
// СТОП - Проблема неосуществима
8 еще
// Вычислить длину шага t с помощью (3.36) и определить,,,ограничение
j с помощью (3.41) и установите:
9 µ i ← µ i + t v i , i ∈ A
10 µ r ← µ r + t
// Снять ограничение j из A
11 A ← A \ j
12 конец
13 еще
// Вычислите длину шага t 1 с помощью (3.36)и t 2 (3.39), чтобы определить
ограничение j через (3.41)
14 если t2 ≤ t1 ,то
// Сделать шаг
15 w ← w + t2p
16 µ i ← µ i + t2в i
17 µ r ← µ r + t2
// Добавить ограничение r к A
18 A ← A ∪ r
19 еще
// Сделать шаг
20 w ← w + t1p
21 µ i ← µ i + t1в i
22 µ r ← µ r + t1
// Снять ограничение j из A
23 A ← A \ j
24 конец
25 конец
26 конец
27 конец
4. Проверка метода
В этой главе описываются процедуры проверки и результаты реализации метода, описанного в главе 3.
4.1. Настройка
Для проверки расширенный планировщик ссылок был реализован численно в MATLAB версии 9.3 (2017b) [38]. MATLAB был выбран для этой реализации из-за к его доступности и компетентности в области алгоритмов и численного анализа.
Работа метода сначала рассмотрена на примере 3-призмы, которая является простейшей формой структуры тенсегрити (рис.1.2а и рис. 4.1). Её простота обеспечивает чёткое представление информации (когда количество элементов в тенсегрити увеличивается, структура быстро усложняется). 3-призма состоит в общей сложности из двенадцати элементов, из которых три являются стержнями, а девять - безмассовыми тросами. Кроме того, узлы 1, 2 и 3 на рис. 3.1 были привязаны к своему исходному положению. Для при этой проверке узлы 4, 5 и 6 не были ограничены. В таблице 4.1 перечислены некоторые общие цифры-ical значения, используемые для этой реализации. Эти значения основаны на прототипе рабочего стола состоит из стержней из полимолочной кислоты и тонких струнных тросов. В таблице 4.2 приведены настройки параметров используется для полнотекстового планировщика ссылок и его расширения SQP. Обратите внимание, что если алгоритм сходится, все предписанные траектории точно отслеживаются FBRP.








