ПРЕДЛОЖЕНИЕ 6.2.1. Плоский выпуклый многоугольник из стержней и тросов является жёстким тогда и только тогда, когда он является жёстким первого порядка.
Доказательство. Пусть p’ — любое нетривиальное изгибание первого порядка многоугольника b-c G(p). Если G(p) не имеет ненулевого собственного напряжения, то согласно стресс-тесту первого порядка мы можем выбрать p' такое, что (pi — pj)(pi’ —pj’) < 0 для всех тросов (i, j). Если w — любое собственное ненулевое собственное напряжение для G(p), то согласно [7] соответствующая матрица напряжений Ω является отрицательно полуопределённой только с аффинными движениями в ядре. Согласно выпуклой природе многоугольника и связности, легко проверить, что (p’)TΩp' # 0 и (p’)TΩp' < 0. Таким образом, с помощью стресс-теста второго порядка Следствия 5.2.1 p' распространяется на изгиб второго порядка (p', p"), который является строгим для всех тросов. Но подкаркас G0(p) в G(p), состоящий только из стержней, является просто выпуклым многоугольником и поэтому независим. Предложение 6.1.1 показывает, что существует изгиб p(t) в группе G(p) такой, что Dt [p(t)]│t=0 = p’ и Dt2[p(t)]│t=0 = p’’. Но поскольку (p', p") является строгим для всех тросов, то p(t) не является также нетривиальным непрерывным изгибом для G(р). Таким образом, G(p) не является жёсткой, что доказывает утверждение.
C ледствие 6.2.2. Если плоский выпуклый многоугольник из стержней и тросов типа b - c с v вершинами имеет менее v-2 тросов, то он не является жёстким.
Доказательство . Чтобы тенсегрити-каркас имел бесконечно малую жёсткость, необходимо по меньшей мере v-2 тросов.
Замечание 6.2.1. Когда кто-то пытается напрямую показать, что конкретный выпуклый многоугольник из стержней и тросов типа b-c не является жёстким на плоскости, то может возникнуть соблазн сделать некоторые из напряжённых тросов стержнями, чтобы уменьшить «степени свободы» и упростить расчёт. Например, каркас G(p) на Рис. 19, полученный заменой двух тросов на Рис. 14а стержнями, не является жёстким (но если заменить распоркой или стержнем горизонтальный трос, то такой каркас станет жёстким).
Подкаркас Go(p), состоящий только из стержней, независим. G(p) имеет изгиб первого порядка, а из соображений первого порядка, как показано в [1], Go(p) имеет непрерывный изгиб. При этом изгибе длина горизонтального троса не может увеличиваться (согласно [7]), а остальные длины тросов уменьшаются строго по первой производной. Таким образом, мы получаем непрерывный изгиб G(p).
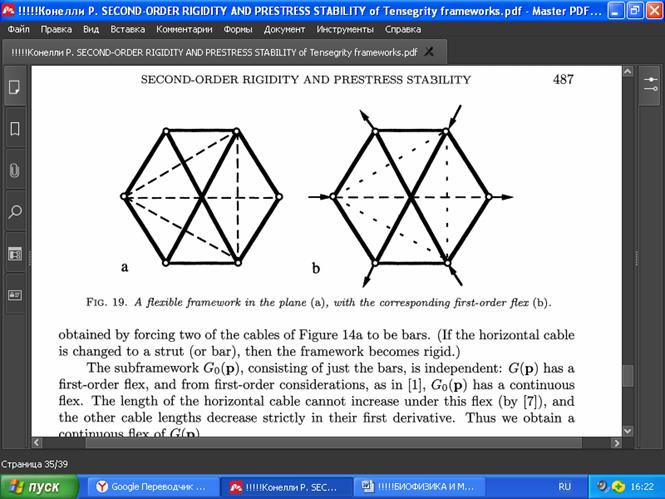
РИС. 19. Гибкий каркас в плоскости (а) с соответствующим изгибом первого порядка (б).
Тем не менее, нужно быть осторожным, решая, какой из тросов должен быть стержнем. Например, рассмотрим структуру на Рис. 20а.
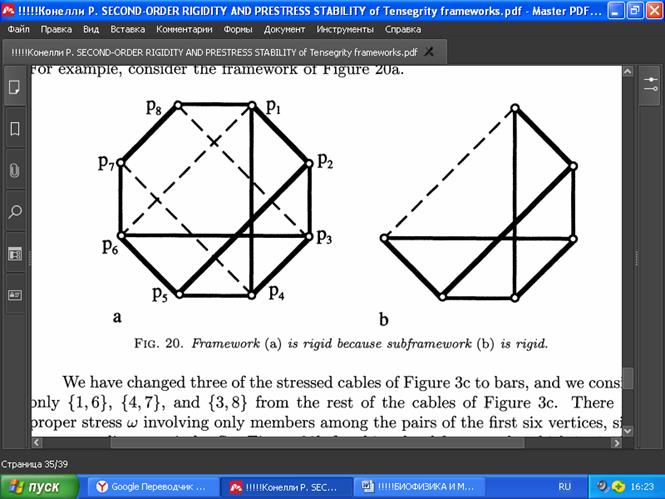
РИС. 20. Каркас (а) является жёстким, потому что его подкаркас (b) является жёстким.
В этом примере мы заменили только три напряжённых троса (1,6), (4,7) и (3,8) на стержни (Рис. 3c). При этом имеется собственное напряжение w, включающее только элементы среди пар первых шести вершин, так как p1,..., p6 лежат на окружности (см. Рис. 20b подкаркаса b-c этой структуры, который согласно [7] является жёстким). Если рассматривать p1, p3, p4 и p6 как жёсткое закреплённое подмножество вершин, то вершины p1, p3, p4, p6, p7, p8 определяют каркас c бесконечно малой жёсткостью. Таким образом, весь каркас G(p) на Рис. 20а является жёстким. С другой стороны, подкаркас в G(p), определяемый только стержнями, независим, как в нашем доказательстве гипотезы Рота. Кроме того, все собственные напряжения на Рис. 3c также являются собственными собственными напряжениями G(p), и существует нетривиальный изгиб первого порядка p’ на Рис. 3c, который является нетривиальным изгибом первого порядка G(p). Почему тогда мы не можем заключить, как мы сделали при доказательстве гипотезы Рота, что G(p) является гибкой, путём расширения p' до строгого изгиба второго порядка (p', p") (используя строгий тест напряжений второго порядка в Cледствии 5.2.1)? Причина, по которой мы не можем применить стресс-тест второго порядка, заключается в том, что мы должны учитывать все правильные собственные напряжения G(p), а не только те, которые видны из Рис. 3c. Ведь, на самом деле, при добавлении стержней G(p) будет иметь больше внутренних напряжений, которые необходимо учитывать. При учёте этих добавленных напряжений оказывается, что G(p) устойчива даже к предварительному напряжению.
Мораль здесь заключается в том, что если кто-то хочет добавить внутренние стержни, как на Рис. 19, и сохранить при этом гибкость каркаса, то нужно не только следить за тем, чтобы добавленные стержни сохраняли независимость стержневого подкаркаса и не разрушали бесконечно малые изгибы, но также убедиться в том, что новые стержни не вносят новых собственных напряжений во весь каркас.
Приложение. ПРИНЦИПЫ ЗАМЕНЫ ЭЛЕМЕНТОВ.
П.1. От стержневых каркасов до каркасов из тросов и распорок.
Напомним из § 2.3, что если стержневой каркас имеет бесконечно малую жёсткость при ненулевом собственном напряжении, то мы можем заменить некоторые стержни тросами и распорками, следуя знакам собственного напряжения (подробнее см. [29]). Аналогично, как следует из §3.4, если стержневой каркас устойчив к предварительному напряжению с нетривиальным собственным напряжением w, то мы можем заменить некоторые стержни тросами или распорками, следуя знакам этого собственного напряжения w.
Однако, у нас нет такого принципа замены для жёсткого стержневого каркаса второго порядка. Если каркас не устойчив к предварительному напряжению, то мы должны проверить знаки всех напряжений, используемых для блокировки конуса изгибов первого порядка: если все они совпадают по определённому знаку, то соответствующий стержень можно заменить, сохранив при этом жёсткость второго порядка.
Итак, для каркаса, который является жёстким, нам пока неизвестен общий принцип замещения по какому-то другому критерию. Далее мы покажем, как можно заменять тросы и распорки стержнями.
П.2. Эквивалентные стержневые каркасы для структур, устойчивых к предварительному напряжению.
Рассматривая структуру каркаса тенсегрити из тросов и распорок, мы всегда можем заменить все элементы стержнями, поскольку эта замена, конечно, сохранит любую жёсткость каркаса. Однако, на самом деле, это может увеличить жёсткость, превратив нежёсткий каркас в жёсткий, жёсткий каркас второго порядка - в каркас, устойчивый к предварительному напряжению, а устойчивый к предварительному напряжению каркас - в жёсткий каркас первого порядка. Поэтому необходим более деликатный принцип замены, при котором жёсткость, устойчивость к предварительному напряжению или жёсткость второго порядка сохраняются неизменными.
Свяжем с тенсегрити-структурой специальную стержневую структуру, которая не зависит от фиксации собственного напряжения. Предположим, что некоторый каркас G(p) имеет трос {i, j} с pi # pj. Мы можем заменить этот трос двумя стержнями (i,k) и (k,j), расположив pk на открытом отрезке между pi и рj, чтобы получить структуру на Рис. 21а. Точно так же распорку (i, j) можно заменить двумя стержнями (i,k) и (k, j), только теперь узел pk должен лежать на прямой, проходящей через pi и рj, но вне замкнутого отрезка между pi и рj (Рис. 21b). Назовём вышеперечисленные процессы разделением троса и разделением распорки соответственно. Понятно, что такие расщепления не меняют жёсткости каркаса в Rd при d ≥ 2, однако любое такое расщепление создаёт каркас, который не является жёстким первого порядка. И мы можем разделить все тросы и распорки G(p), чтобы создать то, что будем называть эквивалентным стержневым каркасом G-(p-), который является жёстким тогда и только тогда, когда G(p) является жёстким.
Рассмотрим взаимосвязь между разделяющими элементами и устойчивостью к предварительному напряжению. Предположим, что w — собственное напряжение для каркаса тенсегрити G(p), а (i, j) — трос или распорка G. Предположим, что G(p) разделён вдоль элемента (i, j) в точке pk (Рис. 21).
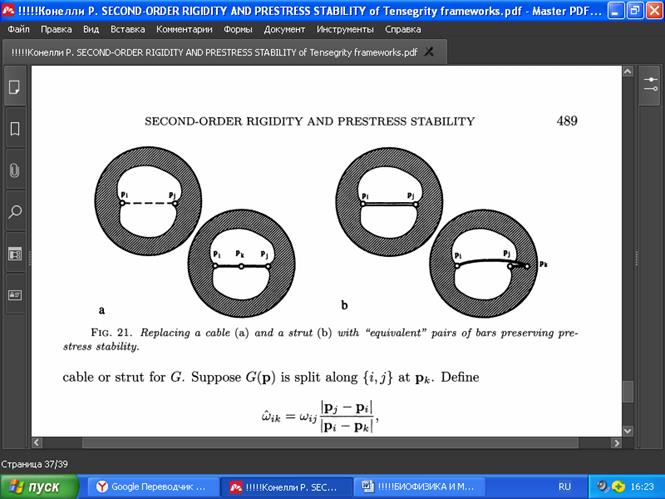
РИС . 21. Замена троса (а) и распорки (б) «эквивалентными» парами стержней, сохраняющими устойчивость к предварительному напряжению.
Определим
wik- = wij │pj – pi│/│pi – pk│
wjk- = wij │pj – pi│/│pi – pk│ для wij > 0
–wij pj – pi│/│pi – pk│ для wij < 0
и wlm- = wlm при (l,m) # (i,k) и (l,m) # (j,k), где pj находится между рi и pk, когда wij < 0. Легко проверить, что определённое таким образом w- является собственным напряжением расщеплённого каркаса G(p).
ПРЕДЛОЖЕНИЕ A.2.1. Пусть G(p) — любой каркас тенсегрити со строгим собственным напряжением w. Пусть G-(p-) — каркас, расщеплённый по любому тросу или стойке. Тогда w стабилизирует G(p) тогда и только тогда, когда w- стабилизирует G-( p -).
Доказательство. Согласно Предложению 3.4.2, нужно рассмотреть только пространство изгибаний первого порядка p' группы G(p), дополнительных к тривиальным изгибам первого порядка, а затем вычислить их в форме, определяемой Ω. То же самое будет справедливым для G-(p-).
Согласно стресс-тесту первого порядка, так как wij # 0, то мы знаем, что (pi — pj)(pi’ — pj’) = 0. Добавив тривиальный изгиб первого порядка p', мы можем рассмативать некоторое пространство изгибов первого порядка G(p), имеющее pi’ = рj’ = 0. Аналогично, для G-(p-) можно рассматривать только те изгибы первого порядка p-', которые являются прямой суммой p' на вершинах G(p) и pk’ перпендикулярно pi - pj, где k является расщепляющей вершиной. Оценим Ω- в p-’:
(p-’)TΩ-p-’ = ∑lm wlm-│pl-‘ — pm-‘│2 = ∑lm│pl-‘ — pm-‘│2 + wlk│pk‘│2 + wjk│pk‘│2 = (p’)TΩp’
Легко проверить, что wik + wjk > 0 (для тросов, для распорок с обратным знаком). Таким образом, Ω- положительно определена на дополнительном пространстве нетривиальных изгибов первого порядка тогда и только тогда, когда Ω положительно определена в соответствующем пространстве.
Следствие A.2.2. Пусть G(p) — любой тенсегрити-каркас, а G-( p -) — эквивалентный стержневой каркас, полученный разделением всех тросов и распорок ненулевой длины. Тогда G(p) устойчив к предварительному напряжению со строгим собственным напряжением тогда и только тогда, когда G-(p-) устойчив к предварительному напряжению.
Таким образом, при желании можно «свести» задачу определения устойчивости каркаса к предварительному напряжению к случаю, когда все элементы являются стержнями.
П.3. Эквивалентные стержневые каркасы с жёсткостью второго порядка.
Если у нас есть тенсегрити-каркас без строгого собственного напряжения, как на рис. 9b, то замена его эквивалентной парой стержней может разрушить жёсткость второго порядка (но не жёсткость). Например, на рис. 22 показан изгиб второго порядка.

РИС. 22. Гибкость второго порядка (но жёсткого) стержневого каркаса, эквивалентного жёсткому каркасу тенсегрити второго порядка.
Если ограничиться тенсегрити-каркасами, в которых все тросы и распорки имеют ненулевые коэффициенты некоторого собственного напряжения, то для проверки жёсткости второго порядка можно переключиться на эквивалентный стержневой каркас








