ПРЕДЛОЖЕНИЕ 5.1.1. Существует вектор-столбец x ? R d такой, что

Дата: 2025-04-30; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

A ₀ x = 0

A ₊ x < 0

тогда и только тогда, когда для всех векторов-строк у ? R ^e , у = (у0, у+) таких, что

y ₀ A ₀ + y ₊ A ₊ = 0

y ₊ ≥ 0

выполняется y ₊ = 0.

Это частный случай принципа двойственности для однородных линейных равенств (например, см. [32, теор. 6]). Заметим, что здесь импликация «только если» проста, так как если A₀x = 0, A₊x < 0, y₀A₀ + y₊A₊ = 0, y₊ ≥ 0, то 0 = y₀A₀x + y₊A₊x ≤ 0. Если y₊ # 0, это даёт строгое неравенство и, следовательно, противоречие. Другая импликация неявно или явно использует принцип «разделения гиперплоскостей» (например, см. [17, с.10]). Важным моментом здесь является строгость неравенств, однако, в дальнейшем мы сосредоточимся вместо этого на самом принципе двойственности, отложив на время свойства строгости.

Зададим вектор-столбец

b = b₀ ? R^e

b₊

ПРЕДЛОЖЕНИЕ 5.1.2. Существует вектор-столбец x ? R ^d такой, что

A ₀ x = b ₀

A ₊ x ≤ b ₊

тогда и только тогда, когда для всех векторов-строк y ? R ^e , y = (y0,y+) таких, что

y ₀ A ₀ + y ₊ A ₊ = 0,

y ₊ ≥ 0

выполняется y ₀ b ₀ + y ₊ b ₊ ≥ 0.

Заметим, что здесь тоже вывод «только если» прост, поскольку при A₀x = b₀, A₊x ≤ b₊, y₀A₀ + y₊A₊ = 0 и y₊ ≥ 0, то 0 = y₀A₀x + y₊A₊x ≤ y₀b₀ + y₊b₊, и снова импликация «если» следует из принципа разделения гиперплоскостей.

В терминологии линейного программирования, это предложение является асимметричной формой двойственности в частном случае, когда основная задача имеет постоянную (нулевую) целевую функцию (например, см. обсуждение различных форм альтернативы Фаркаша и доказательства в [15]).

Теперь уточним это предложение, чтобы получить эквивалентную двойную переформулировку и определить, когда имеет место строгое неравенство. Для этого зафиксируем А и В.

ПРЕДЛОЖЕНИЕ 5.1.3. Существует вектор-столбец x ? R ^d такой, что

A ₀ x = b ₀

A ₊ x < b ₊

тогда и только тогда, когда для всех векторов-строк y ? R ^e , y = (y0,y+) таких, что

y ₀ A ₀ + y ₊ A ₊ = 0

y ₊ ≥ 0

выполняется y₀b₀ + y₊b₊ ≥ 0, которое является равенством тогда и только тогда, когда y₊ = 0.

Доказательство. Опять же, если A₀x = b₀, A₊x < b₊, y₀A₀ + y₊A₊ = 0 и y≥ > 0, то 0 = y₀A₀x + y₊A₊x ≤ y₀b₀ + y₊b₊, и мы получаем строгое неравенство и противоречие тогда и только тогда, когда y₊ # 0.

Чтобы доказать обратное, воспользуемся двумя предыдущими предложениями. Предположим, что условия для вектора y выполнены. Согласно Предложению 5.1.2, существует x ? R^d такой, что A₀x = b₀, A₊x ≤ b₊. Если все неравенства для b₊ строгие, то доказательство окончено. Если нет, то отбросим эти строгие неравенства из A, чтобы получить условия A₀x = b₀, A₊x = b₊. Аналогично можно отбросить соответствующий набор переменных в векторе y. Тогда по-прежнему будет верным, что если y₀A₀ + y₊A₊ = 0, то y₀A₀x + y₊A₊x = y₀b₀ + y₊b₊ = 0. Таким образом, применимо Предложение 5.1.1 и существует (малое) x_е ? R^e такое, что А₀х_е = 0, А₊х_е < 0. Тогда А₀(х + х_е) = b₀, А₊(х + х_е) < b₊. Если x_е достаточно мал, то x + x_е по-прежнему удовлетворяет тем неравенствам, которые также были отброшены. Что и требовалось доказать

5.2. Объяснение стресс-теста (теста напряжений).

Применим результаты раздела 5.1 для матрицы жёсткости. Пусть G(p) — каркас тенсегрити в R^d, а R(p) — его матрица жёсткости с размерами dxe. Пусть R₀(p) обозначает её строки (рассматривается как меньшая матрица), соответствующие стержням G, а R₊(p) - подматрица из строк R(p), соответствующих тросам и стойкам G, причём для распорок строки умножены на -1. Пусть w — собственное напряжение G(p), то есть wR(p) = 0. Аналогично представим w = [wo, w+], где w0 соответствует напряжениям на стержнях, а w+ — напряжениям на тросах и распорках (с обратным знаком для последних). Правильному w соответствует w+ ≥ 0, а наличие собственного напряжения означает, что w₀R(p) + w₊R₊(p) = 0.

В рассматриваемой терминологии, p’ является изгибом первого порядка, если

R₀(p)p’ = 0

R₊(p)p’ ≤ 0

и p’, p’’ является изгибом второго порядка, если вместе с тем выполняются

R₀(p’)p’ + R₀(p)p” = 0,

R₊(p')p’ + R₊(p)p” ≤ 0

где неравенство выполняется только тогда, когда соответствующее неравенство для системы первого порядка является равенством. Напомним, что p” (или p’) является строгим для троса или распорки (i, j), если соответствующее неравенство является строгим.

Теперь получим строгое условие двойственности второго порядка.

СЛЕДСТВИЕ 5.2.1 (тест напряжений второго порядка). Изгиб первого порядка p ' для G ( p ) переходит в изгиб второго порядка ( p ', p ") тогда и только тогда, когда для всех собственных внутренних напряжений w в G ( p ) с матрицей напряжений Ω

( p ’)Ω p ’ ≤ 0.

Кроме того, p " может быть выбрано строгим на каждом тросе и распорке ( i , j ), где p ' не является строгим, тогда и только тогда, когда для всех правильных собственных напряжений w выполнение p ' Ω p ' = 0 влечёт выполнение wij = 0 для каждого такого элемента ( i , j ).

Доказательство. Применим Предложение 5.1.3 при

p = x

R₀(p) = A₀, −R₀(p')p’ = b₀,

R₊(p) = A₊, −R₊(p')p’ = b₊,

w₀ = y₀, w₊ = y₊.

Без ограничения общности можно предполагать, что R(p)p’ = 0, так как для любого троса и распорки p’ является строгим и для них можно пренебречь условиями второго порядка. Условия второго порядка переводятся в гипотезу Предложения 5.1.2, а его заключение переводится в условие, что w является правильным собственным напряжением. Тогда

0 < y₀b₀ + y₊b₊ = −w₀R₀(p')p’ − w₊R₊(p')p' = −wR(p')p’ = −(p')^ТΩp’

является искомым условием, что строго следует из Предложения 5.1.3.

Можно ещё больше упростить рассмотрение, если G состоит только из стержней, тогда получим двойственность второго порядка для стержневых каркасов.

СЛЕДСТВИЕ 5.2.2 ( c тресс-тест второго порядка для стержневых каркасов). Изгиб первого порядка p ’ стержневого каркаса G ( p ) переходит в изгиб второго порядка тогда и только тогда, когда для всех собственных напряжений w для G ( p ) с матрицей напряжений Ω

(p’) ^Т Ωp’ = 0.

Замечание 5.2.1. В приложении показано, что всегда можно заменить каркас (со строгим собственным напряжением) на эквивалентный стержневой каркас и использовать его для проверки жёсткости второго порядка. Однако, проще использовать Следствие 5.2.1 напрямую, чем вводить столько посторонних элементов.

5.3. Жёсткость второго порядка и устойчивость к предварительному напряжению.

Когда жёсткость второго порядка подразумевает устойчивость к предварительному напряжению? Мы начнём со случаев, когда множество собственных напряжений или множество равновесных изгибов первого порядка является одномерным, т.е. естественными начальными для рассмотрения случаями.

Заметим, что для фиксированной системы (каркаса, структуры) тенсегрити G(p) собственное напряжение и изгибы первого порядка образуют конус с началом в вершине конуса.

ПРЕДЛОЖЕНИЕ 5.3.1. Если каркас тенсегрити G ( p ) является жёстким второго порядка, либо имеет одномерный конус равновесных изгибов первого порядка, либо имеет одномерный конус собственных напряжений, то G ( p ) устойчив к предварительному напряжению.

Доказательство . Пусть р’ — любое нетривиальный равновесный изгиб первого порядка G(p), порождающий одномерный конус всех равновесных изгибов первого порядка. Если для всех собственных напряжений w с матрицей напряжений Ω

t²(p’)^ТΩp’ = (tp')^ТΩtp’ ≤ 0

для всех изгибов tp' первого порядка G(p) (где t — вещественный скаляр), то по Следствию 5.2.1 p' продолжается до изгиба второго порядка (p',p") G(p). Но это противоречит условию, поэтому G(p) является жёсткой второго порядка. Таким образом, для некоторого собственного напряжения w при (p’)^ТΩp’ > 0 оно стабилизирует G(p), согласно Предложению 3.4.2, и G(p) устойчива к предварительному напряжению.

Пусть w — ненулевое собственное напряжение в одномерном конусе собственных внутренних напряжений. Предположим, что существует нетривиальный изгиб первого порядка p' такой, что (p’)^ТΩp’ ≤ 0. Если −w не является собственным напряжением, тогда tw, t ≥ 0 являются только правильными собственными напряжениями G(p). Тогда, согласно Следствию 5.2.1, G(p) снова не будет жёсткой второго порядка, что противоречит условию. Следовательно, либо (p’)^ТΩp’ > 0 для всех нетривиальных изгибов первого порядка p’, либо −w является правильным собственным напряжением G(p). Если -w - правильное собственное напряжение, то (p’)^ТΩp’ = 0, и p' снова будет переходить в изгиб второго порядка. Таким образом, (p’)^Т(±Ω)p’ > 0 и ±w стабилизирует G(p).

Мы уже рассматривали пример тенсегрити-каркаса на плоскости (Рис. 9b), который, как легко видеть, является жёстким второго порядка, что прямо следует из определения, но не является устойчивым к предварительному напряжению при любом собственном напряжении. Теперь как пример расчёта с использованием стресс-теста рассмотрим стержневой каркас в трёхмерном пространстве. Если G(p) - стержневой каркас, пусть

p'(1),..., p'(n)

обозначают базис пространства нетривиальных изгибов первого порядка группы G(p). Пусть

Ω(1),..., Ω(m)

обозначает базис пространства собственных напряжений группы G(p). Если G(p) устойчива к предварительному напряжению, то некоторая линейная комбинация матриц напряжений должна быть положительно определённой на пространстве, порождённом изгибами первого порядка p’(1),...,p’(n). Согласно Следствию 5.2.2 стресс-теста второго порядка для стержневых каркасов, G(p) не является жёстким второго порядка тогда и только тогда, когда все матрицы напряжений имеют общий ненулевой вектор, на котором они оцениваются как равные 0 в той же самой пространство, порожденным p'(1),..., p'(n). При n = 2 оба этих критерия можно проверить с помощью некоторых легко вычисляемых выражений. Рассмотрим конкретный пример.

ПРИМЕР 5.3.1. Пусть G(p) — стержневой каркас в трёхмерном пространстве с семью вершинами (Рис. 17а):

p1 = (0,0,0), p4 = (1,0,0), p7 = (1,0,0)

p2 = (0,1,0), p5 = (1,1,0),

p3 = (0,0,1), p6 = (0,1,0),

(хотя p2 = p6 и p4 = p7, на рисунке мы немного разделили их для понимания схемы) и распорками:

(1,2), (1,3), (1,4), (1,6), (1,7),

(2,3), {2,5}, (2,7),

(3,4), (3,5),

(4,5), (4,6),

(5,6), (5,7),

(6,7).

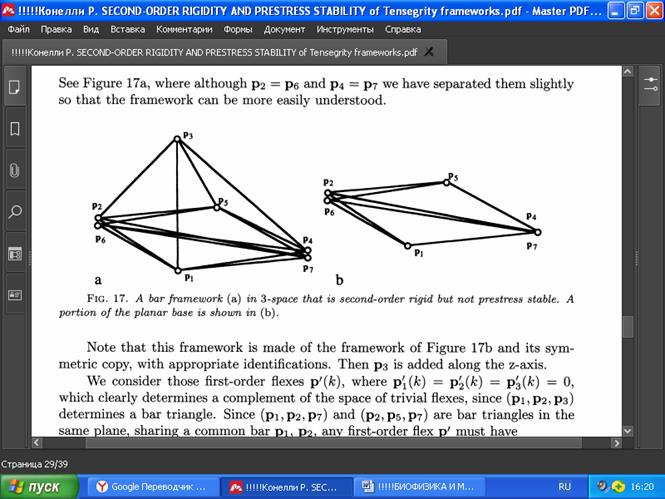
РИС . 17. Стержневой каркас (а) в трёхмерном пространстве, который является жёстким второго порядка, но не устойчивым к предварительному напряжению. На (b) показана часть плоского основания.

Заметим, что этот каркас состоит из каркаса, показанного на Рис. 17b, и его симметричной копии с соответствующими обозначениями, также добавлена p3 на оси Z.

Рассмотрим изгибы первого порядка p'(k) такие, что p1'(k) = p2'(k) = p3'(k) = 0, что, очевидно, определяет дополнение пространства тривиальных изгибов, так как (p1, p2, p3) определяет стержневой треугольник. Так как (p1, p2, p7) и (p2, p5, p7) являются треугольниками со стержнями в одной плоскости, имеющими общий стержень (p1, p2), при любом изгибе первого порядка p' должно выполняться

(p1 − p5)(p1’ − p5’) = 0.

Другими словами, (1, 5) — это «подразумеваемая распорка». Таким образом, здесь мы предполагаем жёсткий тетраэдр первого порядка (p1, p2, p3, p5) при p5’ = 0. Аналогично, при p4’ = 0 для предполагаемого тетраэдра (p1, p3, p5, p4) (см. [9]). Таким образом, основой для образования дополнительного пространства являются следующие изгибания (деформации) первого порядка:

pi’(1) = (0,0,1) для i=6

(0,0,0) в других случаях

pi’(2) = (0,0,1) для i=7

(0,0,0) в других случаях

Можно также найти два независимых напряжения G(p):

1 для (i, j) = (2,7), (5,6) или (1,6)

wij(1) = −1 для (i, j) = (2,5), (6,7) или (2,1)

0 в других случаях

1 для (i, j) = (1,7), (5,7) или (4,6)

wij(2) = −1 для (i, j) = (1,4), (6,7) или (4,5)

0 в других случаях

В этом легко убедиться, взглянув на Рис. 17b. Заметим, что е = 15 = 3v − 6 и пространство нетривиальных (равновесных) изгибов первого порядка должно иметь размерность 2, поэтому размерность пространства собственных напряжений также равна 2. Таким образом, w(1) и w(2) показывают все собственные напряжения.

Затем находим матрицы напряжений Ω(1), Ω(2), соответствующие w(1), w(2), относительно векторов p’(1), p’(2). При a = 1,2, b = 1,2, k = 1,2

p’(a)^ТΩ(k)p’(b) = Ω_ab(k) = ∑_ij wij(k) (pi’(a) − pj’(a)) (pi’(b) − pj’(b))

Отсюда

Ω(1) = ∑w6i(1) −w67(1) = 1 +1

−w67(1) ∑w7i(1) +1 0

Ω(2) = ∑w6i(2) −w67(2) = 0 +1

−w67(2) ∑w7i(2) +1 1

Чтобы увидеть, является ли любая линейная комбинация из них положительно определённой, найдём соответствующие собственные значения λ1, λ2:

det [λ1 Ω(1) + λ2 Ω(2)] = det λ1 λ1+λ2 = −λ1² − λ1λ2 − λ2²

λ1+λ2 λ2

Само это выражение является отрицательно определённой квадратичной формой, так как (−1)² − 4(−1)(−1) = −3 < 0. Таким образом, для каждых (λ1, λ2) # (0, 0) det [λ1Ω(1) + λ2 Ω(2)] < 0, откуда следует, что ни одна из линейных комбинаций λ1Ω(1) + λ2Ω(2) не является положительно определённой и, значит, такие λ1w(1) + λ2w(2) не могут обеспечить устойчивость к предварительному напряжению.

С другой стороны, вспомним, что стресс-тест второго порядка для стержневых каркасов (следствие 5.2.2) говорит, что изгиб первого порядка p' будет распространяться на изгиб второго порядка тогда и только тогда, когда p' находится в нулевом множестве всех собственных напряжений (рассматриваемых как квадратичные формы) G(p). Если какое-то p’ расширяется, то расширяется и p’ плюс любое тривиальное изгибание первого порядка, поэтому мы можем предположить, что p’ находится в пространстве, натянутом на p’(1) и p/(2). Таким образом, G(p) будет жёсткой второго порядка тогда и только тогда, когда Ω(1) и Ω(2) (и, следовательно, все λ1Ω(1) + λ2Ω(2)) имеют общие нули. Нули Ω(1) (как квадратичной формы) скалярно кратны (0,1) или (2,−1). Для Ω(2) мы получаем (1,0) или (−1,2). Ни один из приведённых выше четырёх векторов не является скалярным-кратным любому из других, поэтому каркас G(p) является жёстким второго порядка, но не устойчивым к предварительному напряжению.

Замечание 5.3.1. Если размерность пространства нетривиальных (равновесных) изгибов первого порядка I равна двум, то легко определить, когда каркас устойчив к предварительному напряжению. Вычислив базис матриц напряжений, ограниченный I, и выбирая ортонормированный базис для I, мы видим, что существует не более трёх таких различных матриц напряжений (даже если пространство собственных напряжений имеет большую размерность), поскольку они соответствуют симметричным матрицам размером 2x2. Если таких матриц всего две, можно провести анализ, аналогичный примеру 5.3.1. Если таких матриц напряжений, независимых от I, три, то всегда существует стабилизирующее собственное напряжение.

Например, в примере 5.3.1 можно немного изменять точки, сохраняя в плоскости все точки, кроме p3, и получая тем самым много других примеров жёстких, но не устойчивых к предварительному напряжению стержневых каркасов второго порядка в трёхмерном пространстве. Обратите внимание, что базовый граф в этом примере представляет собой триангулированную сферу. На Рис. 18а показана реализация этого графа в виде триангулированной выпуклой поверхности. Согласно [6], эта реализация также является жёсткой второго порядка. На самом деле, она устойчива также до напряжения. Все элементы, примыкающие к р6 и р7, имеют положительное напряжение при стабилизирующем собственном напряжении. В связи с этим возникает вопрос, все ли триангуляции выпуклого многогранника в трёхмерном пространстве с рёбрами в виде стержней устойчивы к предварительному напряжению? В [6] показано лишь, что такие каркасы являются жёсткими второго порядка. Ответ - положительный, что будет доказано нами в другом месте.

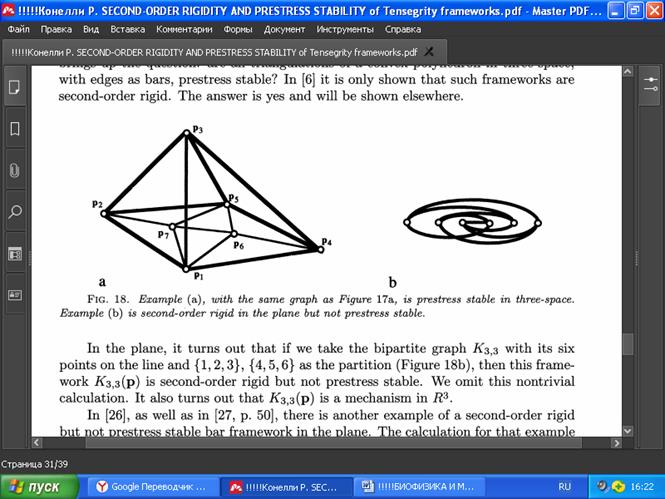
РИС . 18. Пример (а) той же структуры, что и на рис. 17а, но устойчивой к предварительному напряжению в трёхмерном пространстве. Пример (b) жёсткой структуры второго порядка на плоскости, но не устойчивой к предварительному напряжению.

На плоскости оказывается, что если взять двудольный граф K_3,3 с шестью точками на прямой и (1, 2, 3), (4, 5, 6) в качестве разбиения (Рис. 18b), то этот каркас K_3,3(p) является жёстким второго порядка, но не устойчивым к предварительному напряжению (мы опускаем нетривиальное вычисление для этого случая); также оказывается, что K_3,3(p) — механизм в R³. В [26], а также в [27, с. 50] описан ещё один пример жёсткого, но не устойчивого к предварительному напряжению плоского стержневого каркаса второго порядка. Расчёт для последнего примера оказывается довольно простым.

5.4. Приложение результатов к многоугольным структурам из стержней и тросов типа b - c .

Применим стресс-тест второго порядка к особому классу каркасов G(p) - многоугольникам из распорок и тросов типа b-c, описанным в §3.5, то есть G(p) представляет собой плоский выпуклый многоугольник со стержнями в качестве рёбер и тросами внутри.

ПРЕДЛОЖЕНИЕ 5.4.1. Пусть p ’ — любое нетривиальное изгибание первого порядка плоского многоугольника G ( p ) типа b - c . Тогда p ’ продолжается до строгого изгибания второго порядка ( p ’, p ") для G ( p ).

Доказательство . Пусть Ω — любая матрица напряжений для каркаса G(p) c собственным напряжением w. Поскольку p’ нетривиален, то легко проверить, что p’ не является аффинным образом p. Согласно [7],

(p’)^TΩp’ < 0,

так как для перевернутого многоугольника (со стойками внутри) соответствующая матрица (−Ω) является положительно полуопределённой. Таким образом, согласно Cледствию 5.2.1, р' продолжается до строгого изгибания второго порядка (р’, р").

Замечание 5.4.1. Мы воспользуемся этим результатом в следующем разделе, чтобы доказать гипотезу Рота о многоугольниках из стержней и тросов. Интересно (хотя и болезненно!) найти p" непосредственно по p', как показано на Рис. 14. Заметим, однако, что с помощью одного только этого результата можно доказать слабую форму гипотезы Рота: а именно, если р' — нетривиальный изгиб первого порядка многоугольника из распорок и тросов (где внешние рёбра — распорки), то его можно использовать для нахождения также строгого изгиба второго порядка (р’, р’’). Тогда p(t) = p + tp' + 1/2t²p" является изгибом в G(p), что и требовалось.

Единственная проблема, остающаяся для нас в более сильной форме гипотезы Рота, состоит в том, чтобы найти способ обращения со стержнями. Этот вопрос будет рассмотрен отдельно в §6.

5.5. Интерпретация результатов для триангулированных сфер.

Для любой триангулированной сферы G(p) в R³ существует естественное соответствие между изгибами первого порядка p' в G(p) (тривиальными по модулю изгибами первого порядка) и собственными напряжениями w в G(p). Действительно, для каждого ребра (i, j) существует двугранный угол θij, который тоже «меняется» и, следовательно, существует производная θij’. Тогда

wij = θij’ / l pi – pj l для элементов (I, j)

и узлы G(p) имеют собственное напряжение. И наоборот, при заданном внутреннем напряжении можно определить изгиб первого порядка p' с помощью θij’, как указано выше (см обсуждение этого в [16] или [14]). Таким образом, используя Cледствие 5.2.1, для гибкости второго порядка можно сформулировать двойственное условие.

C ледствие 5.5.1. Изгиб первого порядка p' триангулированной сферы G(p) в R ³ продолжается до изгиба второго порядка тогда и только тогда, когда для каждого θij’ (возможно, исходя из другого изгиба первого порядка) выполняется

∑ _ij θ ij ’ / lpi – pjl * lpi ’ – pj ’ l ² = 0.

5.6. Интерпретация результатов с точки зрения упаковок.

Для жёстких упаковок ([11], [12]) связанный каркас имеет закреплённые вершины и все его элементы являются распорками. Тогда любое собственное напряжение wij ≤ 0 (для всех распорок (i, j)) и, таким образом, при всех изгибах первого порядка p’

(p')^TΩp’ = ∑_ij wij (pi’ – pj’)² ≤ 0,

так как на закреплённых вершинах можно принять p' = 0. В предположении связности G при p' # 0 мы получаем строгое неравенство. Таким образом, существует строгий изгиб второго порядка (p', p"), и легко видеть, что такой каркас G(p) является жёстким тогда и только тогда, когда он жёсткий первого порядка (это было непосредственно показано в [11]).

6. ОБОБЩЕНИЕ ДЛЯ ДЕФОРМАЦИЙ ВТОРОГО ПОРЯДКА.

6.1. Общий итог.

Некоторые изгибания второго порядка распространяются на непрерывные изгибания каркаса. Например, если изгиб второго порядка укорачивает все тросы и удлиняет все распорки, а стержней нет, то ясно, что мы можем дополнить эти первые две производные реальным аналитическим путём. Мы описываем менее ограничительную ситуацию, когда мы ещё можем расширить гибкость второго порядка. Этот результат является расширением предыдущих и мотивирован некоторыми результатами из [1, 2].

Стержневой каркас G(p) называется независимым, если единственным собственным напряжением для G(p) является нулевое собственное напряжение.