Каркас тенсегрити является жёстким второго порядка, если все изгибы второго порядка (p', p") имеют p' тривиальным изгибом первого порядка, в противном случае G(p) является гибким второго порядка.
На Рис. 16 показаны изгибы (движения) второго порядка некоторых каркасов тенсегрити (двойные стрелки - для p’’, одиночная стрелка - для p’). Изгиб на рис. 16а нетривиален для p’. Изгиб на рис. 16b тривиален для p'/, но (p', p") не является первой и второй производной жёсткого движения p. Изгиб на рис. 16с является производной жёсткого движения р. На рис. 16d показан нетривиальный изгиб второго порядка каркаса, который всё ещё остаётся жёстким.
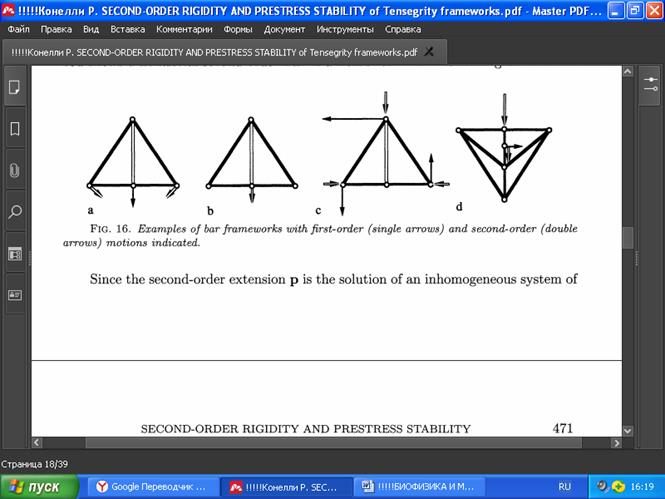
РИС . 16. Примеры каркасов из стержней с движениями первого порядка (одиночные стрелки) и второго порядка (двойные стрелки).
Поскольку расширение второго порядка p является решением неоднородной системы уравнений и неравенств, мы можем добавить к p’’ любое решение q' соответствующей однородной системы.
ПРЕДЛОЖЕНИЕ 4.1.2. Если ( p ’, p ”) является изгибом второго порядка структуры тенсегрити G ( p ) и q ' - любой изгиб первого порядка G ( p ), то ( p ', p ” + q ') является изгибом второго порядка G ( p ).
Доказательство. Предположим, что для каждого троса (i, j) (аналогично доказывается для каждого стержня и распорки) при (pi – pj)(pi’ – pj’) = 0 выполняются
(pi – pj)(pi’ – pj’) + (pi – pj)(pi’’ – pj’’) ≤ 0 (для стержней и распорок = 0 и ≥ 0)
и
(pi – pj)(qi’ – qj’) ≤ 0 (для стержней и распорок = 0 и ≥ 0 соответственно).
Складывая эти неравенства, получаем:
(pi’ – pj’)(pi’ – pj’) + (pi – pj) [(pi’’+ qi’) – (pj’’+ qj’)] ≤ 0 (для стержней и распорок = 0 и ≥ 0).
Это неравенства в Определении 4.1.1. Если добавить кратное самому себе p' к любому расширению второго порядка p, можно сделать так, чтобы расширение второго порядка также удовлетворяло неравенствам второго порядка даже для тех элементов, у которых (pi – pj)(pi’ – pj’) # 0. Что и требовалось доказать
4.2. Тривиальные движения высшего порядка.
Пусть p(t) = (..., pi(t),...), 0 ≤ t ≤ 1 - аналитический путь в конфигурационном пространстве, где pi(t) E Rd, i = 1,..., v. Следуя [6], будем говорить, что p(t) — тривиальный изгиб, если
p(t) = T(t) p(0) = (T(t)p1(0), T(t)p2(0),..., T(t)pv(0)),
где T(t) — жёсткое движение в Rd, являющееся аналитической функцией t, T(0) = I. В частности, это означает, что мы можем записать T(t)pi = A(t)pi + b(t), i = 1,..., v, где A(t) — ортогональная матрица, b(t) E Rd, а все координаты — вещественные аналитические функции t .
Будем говорить, что p’, p",..., p(k), где p(j) E Rdv, j = 1,..., k, является k -тривиальным изгибом p, если существует тривиальный изгиб p(t) такой, что
Djt p(t) = p(j) для всех j = 1, 2,..., k.
Напомним, что Djt обозначает j-ю производную по t.
Легко проверить, что если p’, p’’,..., p(k) является k-тривиальным изгибом любого каркаса G(p) в Rd, то аналог уравнений (а) из Определения 4.1.1 выполняется для любого j = 1,..., k, так как длины ребер, очевидно, сохраняются до любого порядка k.
Хотя мы дали явное описание k-тривиальных изгибов, оно достаточно длинное, поэтому представляется важным уточнить это понятие, учитывая долгую историю путаницы в этой области. Мы уже знаем, что 1-тривиальные изгибы p’ задаются формулой
Pi’ =Spi + b’, I = 1,..., v.
где S = -SТ — кососимметричная матрица размером dxd, а b’ E Rd (см. [6] или [9]). Известно, что каждая ортогональная матрица A, достаточно близкая к единичной матрице I, может быть записана в виде разложения:
A = eS ≈ 1+ S + 1/2S2 + 1/6S3 + …
где S — кососимметричная матрица, а показанный выше бесконечный ряд сходится. Хорошо известно, что экспоненциальное отображение S ↔ eS переводит касательное к ортогональным матрицам пространство группы Ли, которое является алгеброй Ли группы Ли, в саму группу Ли. Это экспоненциальное отображение тождественно является локальным аналитическим диффеоморфизмом вблизи I. Таким образом, любой аналитический путь A(t) с A(0) = I сводится к пути S(t) в алгебре Ли, причём он сам является аналитическим. Таким образом, A(t) = eS(t). С другой стороны, поскольку e0 = I и, следовательно, S(0) = 0, мы можем записать:
S(t) = t S1+ t2/2 S2+ t3/6 S3 + …,
где каждое S1, S2, ... кососимметрично. Таким образом, мы имеем разложение:
A(t) = I + (t S1+ t2/2 S2+ t3/6 S3 + …) + 1/2 (t S1+ t2/2 S2+ t3/6 S3 + …)2 + …
Переставляя члены, что возможно, поскольку у нас абсолютно сходящийся степенной ряд, мы получаем:
A(t) = I+ t S1+ t2/2 (S2 + S12) + t3/6 (S3 + 3/2 S1S2 + 3/2 S2S1 + S13) + … (5)
Таким образом, каждый из матричных коэффициентов tj/j! даёт параметрическое описание j-й производной A(t) и, таким образом, описание k-тривиального изгиба p. Например, p’, p" является 2-тривиальным изгибом p тогда и только тогда, когда существуют кососимметрические матрицы S1, S2 и b', b" E Rd такие, что
p' = S1p + (b’,...,b’),
p” = (S2 + S12)p + (b”,...,b").
Позже будет удобно «отменять» начальные части изгиба k-го порядка при k-тривиальном изгибе. Таким образом, мы констатируем следующее [6].
ПРЕДЛОЖЕНИЕ 4.2.1. Пусть p ( t ), p (0) = p — аналитический путь в конфигурационном пространстве такой, что
p( j) = Dt j[p(t)]|t=0 , j = 0, 1,..., k
является k-тривиальным. Тогда существует жёсткое движение T(t) E R d , аналитическое по t, такое, что T(0) = I и
Dt j[T(t)p(t)]|t=0 = 0 для всех j = 1,...k.
Доказательство. Проведём индукцию по k. При k = 0 доказывать нечего. Итак, предполагается, что
Dt j[p(t)]|t=0 = p, если i = 0,
0, если I = 1,..., k.
Мы хотим найти T(t) такое, что (k + 1)-я производная также равна 0, предполагая, что первые k + 1 производные являются k-тривиальными.
Ограничимся пространством, натянутым на p1, p2,..., pv. Добавляя сюда перенос, при использовании (5) получим:
b(j) = 0, j = 1,..., k+1,
Sj = 0, j = 1,..., k.
Заметим, что Dt j+1[p(t)]|t=0 = Sk+1p. Зададим T(t) в виде:
T(t) = exp [ −tk+1/(k+1)! Sk+1] = I − tk+1/(k+1)! Sk+1 +...].
Также заметим, что для всех j = 1, 2,... выполняется
Dt j[T(t)p(t)]|t=0 = ∑l=0j j Dt l[T(t)] Dt j-l[p(t)] (6)
l
Но
Dt lT(t)|t=0 = 0, l=1,…, k
−Sk+1, l = k+1.
‘
Таким образом, окончательно
Dt j[T(t)p(t)]|t=0 = Sk+1p − Sk+1p = 0, j = k+1. Что и требовалось доказать.
0, j = 1,…, k
Замечание 4.2.1. Существует несколько способов решения проблемы «нормализации» нескольких первых производных. Один из способов — описанная выше техника. Другой способ — использовать «привязку», как показано в [33] и обсуждается в [9]. Третий способ — использовать метод, описанный в [20] (см. также [9]). Эта нормализация доставляет неудобства, но её удобно использовать для доказательства того, что жёсткость второго порядка приводит просто к жёсткости.
Непосредственным следствием определения k-тривиальности и формулы (5) является следующая лемма.
ЛЕММА 4.2.2. Пусть p ’,…, p ( k ) таково, что p ' = p " =… = p ( k -1) = 0. Тогда p ( k ) является 1-тривиальным изгибом в точке p тогда и только тогда, когда p ', p ’’,..., p ( k ) k -тривиален в p .
Также полезно знать следующее.
ЛЕММА 4.2.3. Пусть p ( t ) — любой аналитический путь в конфигурационном пространстве такой, что p ' = Dt p ( t )| t =0 ,…, p ( k ) = Dt k p ( t )| t =0 . Пусть T ( t ) — любое жёсткое движение в Rd , аналитическое по t ; T (0) = I . Тогда Dt [ T ( t ) p ( t )]| t =0 ,…, Dt k [ T ( t ) p ( t )]| t =0 k -тривиален в p тогда и только тогда, когда p ’,..., p ( k ) k -тривиален в p .
Доказательство . Поскольку T(t) обратимо, то достаточно показать, что если p’,...,p(k) k-тривиальна, то Dt[T(t)p(t)]|t=0 ,…, Dtk[T(t)p(t)]|t=0 k-тривиально. Пусть p(l) = Dt l[T-(t)]|t=0, l=1,...,k для некоторого жёсткого движения T-(t) в Rd, аналитического по t, с T-(0) = I. Но тогда, очевидно,
Dt l[T(t)p(t)]|t=0 = Dt l[T(t)T-(t)p(t)]|t=0, l = 1, ... к
при расширении обеих частей по правилу произведения (6). Но T(t)T-(t) тоже является жёстким аналитическим движением в Rd. Лемма доказана.
4.3. Жёсткость второго порядка предполагает жёсткость.
Выше мы обобщили понятие изгиба второго порядка (подробнее см. в [6]) для жёстких каркасов на общие каркасы тенсегрити. В следующей теореме мы покажем, что нетривиальное аналитическое изгибание структуры тенсегрити порождает изгиб второго порядка (p', p"), первого часть порядка p' которого нетривиальна. Естественная идея состоит в том, чтобы взять первую и вторую производные аналитического изгиба, оценённого в начальной точке. К сожалению, это может не сработать, потому что первая производная аналитического изгиба может быть тривиальной, и тогда нам, возможно, придётся ждать, пока какая-то более высокая производная не станет нетривиальной. Для тросов и распорок мы используем принцип, согласно которому первая ненулевая производная квадрата длины стержня имеет правильный знак.








