ПРЕДЛОЖЕНИЕ 3.3.2. Если тенсегрити-каркас G ( p ) устойчив к предварительному напряжению при собственном напряжении w , то G ( p ) является жёстким.
Доказательство . Свойство положительной определённости H гарантирует строгий локальный минимум по модулю тривиальных изгибов первого порядка p. Так как wij # 0 для всех тросов и распорок G, которые появляются в H*, то их энергетические функции строго монотонны вблизи p. Поэтому здесь можно использовать энергетический принцип, чтобы показать жёсткость G(p).
Замечание 3.3.2. Как мы увидим позже, из Теоремы 4.4.1 следует, если если G(p) устойчив к предварительному напряжению, то он является жёстким второго порядка, а по Теореме 4.3.1 он является жёстким. Однако, приведённое выше доказательство намного проще и нагляднее, поскольку оно является следствием непосредственного использования энергетического принципа.
ПРЕДЛОЖЕНИЕ 3.3.3. Если тенсегрити-каркас G ( p ) является жёстким первого порядка, то он устойчив к предварительному напряжению.
Доказательство . Соответствующий стержневой каркас G-(p), безусловно, является жёстким первого порядка. Тогда R(p)TR(p) имеет в своём ядре только тривиальные бесконечно малые изгибы, или, другими словами, R(p)TR(p) положительно определена на равновесных бесконечно малых движениях, перпендикулярных тривиальным бесконечно малым движениям в Rvd. Согласно [29], существует собственное напряжение w, отличное от нуля на каждом тросе и стойке. Если выбрать w достаточно малым, то Ω + R(p)TR(p) также будет положительно определённым на равновесных бесконечно малых изгибах, ограниченных компактной единичной сферой. Таким образом, G(p) будет устойчивым к предварительному напряжению.
Часто удобно считать, что правильное напряжение w в G(p) является строгим, т.е. wij # 0 для каждого троса или распорки. Однако, если мы рассматриваем подкаркасы (подсистемы) G (p), то для устойчивости к предварительному напряжению нужно рассматривать только строгие собственные напряжения.
Замечание 3.3.3. Пеллегрино и Калладин [28] используют другой анализ жёсткости структур с эффектом предварительного напряжения (самонапряжения) (см. также [4]). Для каркаса G(p) с собственным напряжением w и набором образующих p1’,..., pk’ для дополнительного пространства нетривиальных изгибов первого порядка они добавляют k новых строк в матрицу жёсткости wR(p1’),wR(p2’),..., wR(pk’). Если такая расширенная матрица R*(p,w) имеет ранг vd — d ( d +1)/2, то говорят, что предварительное напряжение w «укрепляет» каркас по модулю положительной определённости неопределённой матрицы. Если R*(p,w) не имеет ранга vd — d ( d + 1)/2 (при условии, что вершины охватывают Rd), то существует нетривиальный изгиб первого порядка p' = ∑ ai pj такой, что wR(pi’)p’ = 0 для всех i =1,..., k. Таким образом, wR(pi’)p’ = 0 и G(p) определённо не является устойчивым к предварительному напряжению для этого собственного напряжения w. В самом деле, легко видеть, что их условие жёсткости эквивалентно требованию, чтобы ранг матрицы a2Ω + R(p)тR(p) был равен vd — d(d+1)/2 при всех достаточно малых а (в предположении, что аффинная оболочка р имеет размерность по крайней мере (d-1)). Матрица, которую они имеют в виду и которая должна быть положительно определённой, должна быть эквивалентной Ω + R(p)TR(p), ограниченной некоторым пространством, дополнительным к пространству тривиальных изгибов первого порядка. Если бы не требовалась положительная определённость, то многие механизмы - например, такие, как коллинеарные параллелограммы - были бы объявлены «жёсткими».
С другой стороны, если имеется одномерное пространство равновесных изгибов первого порядка, то мы увидим, что устойчивость к предварительному напряжению требует ранга R*(p), равного dv — d(d+1)/2, и тогда она совпадает с жёсткостью второго порядка. Интересно, что в работе [28] большинство примеров имеют одномерное пространство равновесных изгибов (см. поправки в [5], а также обсуждение в [22-26], как делать анализ второго порядка).
3.4. Интерпретация результатов с точки зрения матрицы напряжений и квадратичных форм энергии.
Приведём некоторые простые факты о квадратичных формах, которые пригодятся нам позже.
ЛЕММА 3.4.1. Пусть Q 1 и Q 2 — две квадратичные формы в конечномерном реальном (со скалярным произведением) векторном пространстве. Пусть Q 2 положительно полуопределена с множеством нулей K , а Q 1 положительно определена на K . Тогда существует положительное вещественное число a такое, что Q 1 + aQ 2 положительно определена.
Доказательство . Обозначим X компактное множество (сферу) единичных векторов в пространстве со скалярным произведением:
X = {p l p∙p =1}
По условию, нулевое множество Q2 есть
K = {p | Q2(p) = 0}.
Пусть K∩X E N E X — открытая окрестность K в X такая, что
Q1(p) > 0 для всех p E N.
Такое открытое множество N существует, поскольку K∩X компактно, Q1 положительно на K \ K∩X E {0} и, следовательно, Q1 при ограничениях K U X должен иметь положительный минимум m. Возьмём N = {p E X | Q1(p) > m /2}. По тем же причинам существуют вещественные константы c1, c2 такие, что
Q1(p) > c1 для всех p E X,
Q2(p) ≥ c2 > 0 для всех p E X \ N.
Пусть a = │с1│/с2. Для p E N∩X найдём
Q1(p) + aQ2(p) ≥ Q1(p) > 0
Для p E X \ N
Q1(p) + aQ2(p) = Q1(p) + │с1│/с2 Q2(p) > c1 + |c1] > 0.
Таким образом, Q1(p) + aQ2(p) положительно на всём X и, следовательно, положительно определено. Лемма доказана.
Замечание 3.4.1. Заметим, что Q1 может быть неопределённым во всём векторном пространстве, поскольку требуется лишь его положительная определённость на K. Заметим также, что для любой квадратичной формы, заданной симметричной матрицей A, где Q(p) = pTAp, ядро формы A наверняка содержится в нулевом множестве Q. Если Ap = 0, то Q(p) = pTAp = 0. Однако, обратное в общем случае неверно, если A не является положительно полуопределённой. В частности, обратное верно, когда A = R(p)TCR(p) - матрица жёсткости. Тогда
(p*)TR(p)TCR(p) p* = ∑ij cij [(pj* - pi*)(pj - pi)]2 ≥ 0
и ядро A при всех сij > 0 совпадает с множеством нулей её квадратичной формы.
Из сказанного выше ясно, что ядро A — это в точности пространство всех изгибов первого порядка соответствующего стержневого каркаса. Напомним, что G-(p) является соответствующей структурой стержней, заменяющих элементы (тросы и распорки) исходной тенсегрити-структуры G(p). Обозначим пространство изгибов первого порядка G-(p) как
I- = I(G-(p)) = {p’ ? Rvd | (pi – pj)(pi’ – pj’) = 0, где (i, j) - элементы G}.
как линейное подпространство Rvd. Напомним также, что Tp — это пространство тривиальных изгибов первого порядка в точке p (таких, что Tp C I-). Заметим, что если G(p) имеет строгое собственное напряжение, то стресс-тест первого порядка подразумевает, что I=I-.
Приведём способ проверки устойчивости каркаса к предварительному напряжению (тенсегрити), который позже пригодится нам для расчётов. Напомним, что напряжение каркаса w является строгим, если оно отлично от нуля на каждом тросе и стойке.
ПРЕДЛОЖЕНИЕ 3.4.2. Каркас тенсегрити G ( p ) является устойчивым к предварительному напряжению со строгим собственным напряжением w тогда и только тогда, когда связанная с ним матрица напряжений Ω положительно определена на любом подпространстве K C I - , дополнительном к Tp.
Доказательство. Предположим, что Ω + R(p)ТCR(p)] является положительно полуопределённой только с Tp в качестве ядра, где C — диагональная матрица положительных коэффициентов жёсткости. Пусть р' E I-. Тогда R(p)p' = 0 и, значит,
0 ≤ (p’)Т[Ω + R(p)ТCR(p)] p’ = (p')ТΩp’
с равенством тогда и только тогда, когда р' E Тр. Таким образом, Ω положительно определена на К.
Прежде, чем доказывать обратное, заметим, что если р' — любой тривиальный изгиб первого порядка в точке р, то согласно Определению 2.2.2 существует кососимметричная матрица S c размерностm. dxd и вектор t E Rd такой, что рi’ = Spi + t, I = 1,..., v. Тогда
… … …
Ωp’ = ∑j wij (pi’ – pj’) = ∑j wij (Spi – Spj) = S ∑j wij (pi – pj) = 0
… … …
Предположим теперь, что Ω положительно определена на К. Пусть р' E Rvd произвольно. Запишем p' = pT + pK + pE, где pT E Tp, pK E K и pE E E, как (ортогональное) дополнение к I- в Rvd. Поскольку ΩpT = 0 = R(p)pT, то имеем:
(p’)T[Ω + R(p)TCR(p)] p’ = (pK + pE)T [Ω + R(p)TCR(p)] (pK + pE) (4)
Согласно замечанию 3.4.1, ядром R(p)TCR(p) является I- = Tp + K.
Теперь применим Лемму 3.4.1 к внутреннего пространству K + E, где Q1 — квадратичная форма, соответствующая Ω, а Q2 — квадратичная форма, соответствующая R(p)TCR(p). Ядром Q2 является точно K, и мы предположили, что Q1 положительно определена на K. При этом возможно умножить C на положительную константу. Поэтому можно считать, что Ω + R(p)TCR(p) положительно определена на K + E. Из (4) следует, что Ω + R(p)TCR(p) положительно полуопределена с ядром Tp, и G(p) устойчив к предварительному напряжению. Что и требовалось доказать.
3.5. Примеры самонапряжённых устойчивых структур .
Ниже приведены примеры тенсегрити-каркасов, устойчивых к предварительному напряжению, но не имеющих жёсткости первого порядка. Следовательно, утверждение, обратное Предложению 3.3.3, неверно.
В структуре на Рис. 7а присутствует собственное внутреннее напряжение такое, что внешние элементы имеют положительное напряжение, и показан нетривиальный изгиб первого порядка, так что можно применить Предложение 3.4.2. Структура на Рис. 7b устойчива благодаря полученному в [7] результату применительно к паутине. На Рис. 7b можно выбрать положительными значения напряжений также внутренних элементов. В обоих этих примерах существует строгое собственное собственное напряжение, такое, что показанный изгиб первого порядка отличен от нуля только на вершинах стержней, которые имеют положительное собственное напряжение, и данный изгиб первого порядка порождает дополнительное пространство к тривиальным изгибам в пространстве всех изгибов первого порядка. Следовательно, матрица напряжений в этом пространстве положительно определёна, и каркас устойчив к предварительному напряжению.
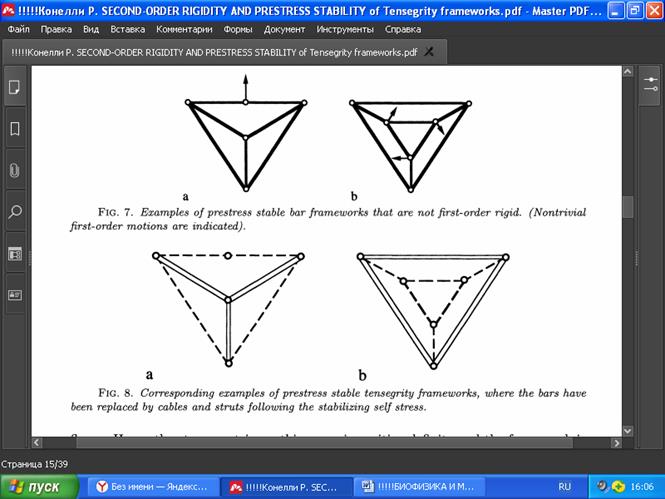
РИС. 7. Примеры предварительно (само-) напряжённых устойчивых стержневых каркасов, которые не являются жёсткими первого порядка (указаны нетривиальные движения первого порядка).
РИС. 8. Примеры предварительно (само-) напряжённых устойчивых каркасов тенсегрити, в которых стержни заменены тросами и распорками после собственного стабилизирующего напряжения.
Согласно примечанию 3.3.1, мы можем заменить соответствующие элементы тросами или распорками и при этом сохранить устойчивость к предварительному напряжению, как показано на Рис. 8.
Может ли каркас, наоборот, быть жёстким, но не устойчивым к предварительному напряжению? Рассмотрим следующие два примера. Прежде заметим, что любой жёсткий стержневой каркас первого порядка без собственного напряжения должен иметь 0 в качестве стабилизирующего собственного напряжения. Пример на Рис. 9а имеет собственное напряжение лишь на части каркаса, а стержень не может иметь напряжения, отличного от 0, поэтому каркас всёё же устойчив к предварительному напряжению. Однако пример на Рис. 9b уже не является устойчивым к предварительному напряжению, потому что короткий горизонтальный трос и горизонтальная стойка не нагружены, и каркас становится нежёстким после их удаления. Тем не менее, каркас явно остаётся жёстким. Будучи построен со всеми элементами в виде стержней, фактически он будет и устойчив к предварительному напряжению.
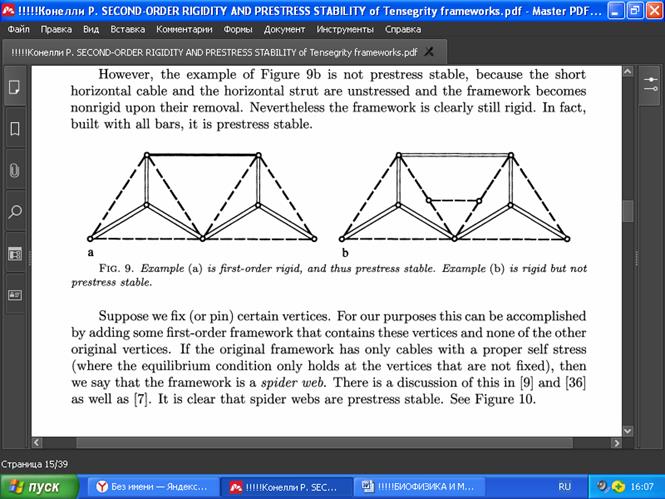
РИС. 9. Пример (а) жёсткой структуры первого порядка и, следовательно, устойчивой к предварительному напряжению. Пример (b) жёсткой структуры, не устойчивой к предварительному напряжению.
Предположим, что мы фиксировали (закрепили) определённые вершины. В нашем случае этого можно добиться, добавив некоторую структуру первого порядка, содержащую эти вершины и не содержащую другие исходные вершины. Если исходный каркас имеет только тросы с надлежащим собственным напряжением (где условие равновесия выполняется только в незакрепленных вершинах), то говорят, что каркас представляет собой паутину (подробно это обсуждается в [9] и [36], а также в [7] для внешнего закрепления). Интуитивно понятно, что паутина устойчива к предварительному напряжению (Рис. 10).
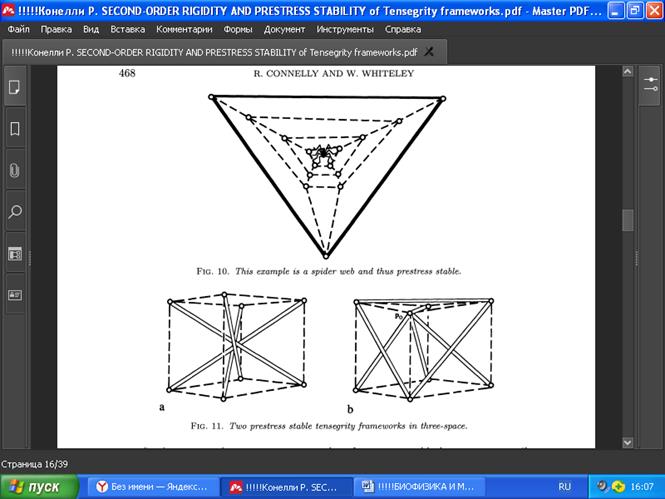
РИС . 10. Самонапряжённая сеть типа паутины (внешние крепления растягивают сеть тросов).
РИС . 11. Две самонапряжённых тенсегрити-структуры в трёхмерном пространстве.
В трёхмерном пространстве возможно много примеров каркасов, устойчивых к предварительному напряжению, но не обязательно бесконечно жёстких каркасов тенсегрити - например, как показано на Рис. 11. На Рис. 11а представлен правильный куб с основными диагоналями в виде распорок и с рёбрами в виде тросов. Примеры типа показанных на Рис. 11b можно получить, если взять любой выпуклый многогранник с треугольной гранью (в данном случае куб с усечённым ближним верхним углом), выбрать точку pg, близкую к этой грани, соединить po со всеми остальными вершинами распорок многогранника и сделать всё ребра многогранника тросами, кроме треугольника, состоящего из распорок. Тогда снова оказывается, что существует строгое собственное внутреннее напряжение w, а Ω положительно полуопределена только с аффинными движениями в ядре. Этот пример тесно связан с трёхмерными сетями («паутинами», см. [36]).
Другой трёхмерный пример можно получить, взяв тетраэдр и поставив распорки на каждую из шести граней, а также предварительно напряженную сеть тросов («паутину») на внутреннюю сторону каждой треугольной грани, как показано на Рис. 12. При этом каждая грань устойчива к предварительному напряжению даже в R3, поэтому сумма функций энергии является положительно полуопределённой только при изгибах первого порядка, которые тривиальны на каждой грани в ядре. Но поскольку сам тетраэдр является жёстким первого порядка, то изгибы, тривиальные на каждой грани, тривиальны и на всём каркасе. Поэтому такой каркас устойчив к предварительному напряжению.
3.6. Гипотеза Рота.
Предположим, что G(p) имеет своими точками вершины плоского выпуклого многоугольника. Если внешние ребра G являются тросами, а все остальные элементы - скажем, распорками, то будем называть такую структуру многоугольником типа «трос-распорка», или многоугольником c - s ( cable - strut ).
Из [7] следует, что любой c-s многоугольник, имеющий собственное внутреннее напряжение w = 0, имеет Ω как положительно полуопределенную только с аффинными движениями в ядре. Оказывается, что аффинные движения никогда не являются изгибами первого порядка таких каркасов [36]. Таким образом, такое w также стабилизирует G(p), и, таким образом, G(p) является жёстким с предварительным напряжением. Заметим, что такой многоугольник c-s не обязательно должен быть жёстким первого порядка. Например, на Рис. 13 шесть вершины лежат на эллипсе, и по классическому результату (см. [3] и [34]) каркас обладает строгим собственным напряжением и нетривиальным изгибом первого порядка. Таким образом, этот каркас устойчив к предварительному напряжению, но не является жёстким первого порядка.
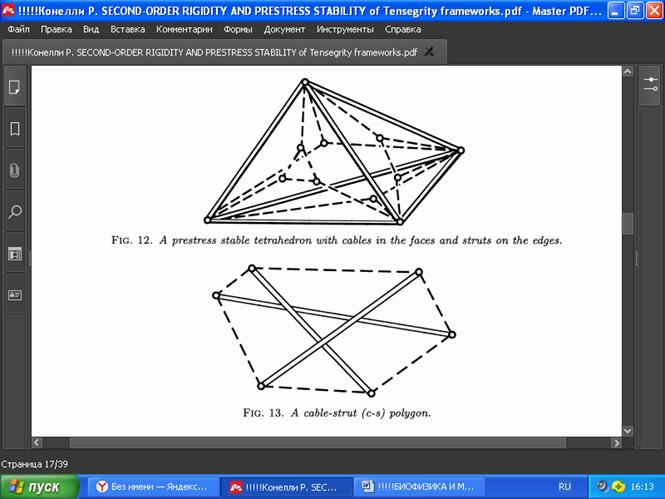
РИС. 12. Самонапряжённый устойчивый тетраэдр с тросами на гранях и распорками по краям.
РИС. 13. Плоская структура из распорок и тросов на основе многоугольника.
С другой стороны, Рот предположил, что любой жёсткий многоугольник типа b-c (стержни снаружи, тросы внутри) является жёстким первого порядка. В §6.2 мы докажем правильность этого предположения. На Рис. 14 показаны три примера нежёстких шестиугольников типа b-c с гибкостью первого порядка.
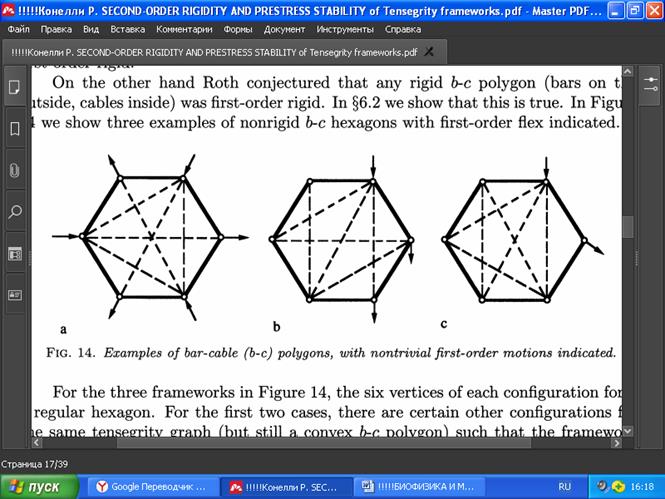
РИС. 14. Примеры многоугольников из стержней и тросов («bar-cable») с указанными нетривиальными движениями первого порядка.
Для трёх каркасов на Рис. 14 шесть вершин каждой конфигурации образуют правильный шестиугольник. В первых двух случаях существуют некоторые другие конфигурации для того же графа тенсегрити (но всё ещё выпуклого многоугольника b-¢), такие, что каркас является жёстким. Однако это не относится к последнему случаю. Читателю предлагается найти непрерывный нетривиальный изгиб каждого из этих каркасов (см. §6.2 для доказательства того, что гибкость существует).
Следуя [29], можно видеть, что существует множество схем соединений тросов, гарантирующих жёсткость первого порядка, как показано на Рис. 15.
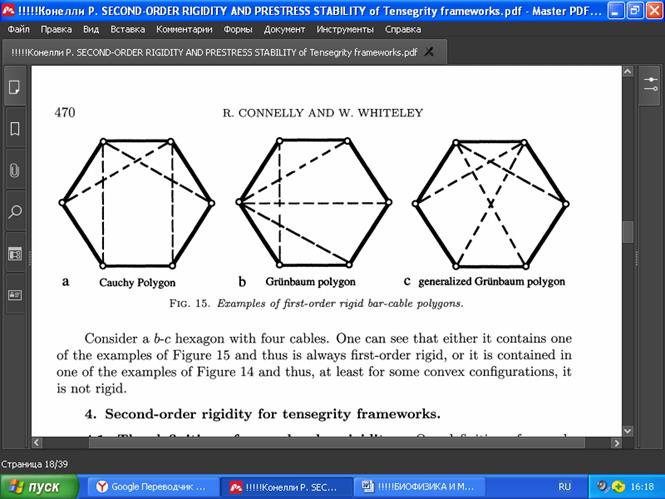
РИС. 15. Примеры жёстких многоугольников первого порядка из стержней и тросов.
Рассмотрим шестиугольник из стержней и тросов (bar-cable) с четырьмя тросами. Можно видеть, что он содержится либо в одном из примеров на Рис. 15 и поэтому всегда является жёстким первого порядка, либо содержится в одном из примеров на Рис. 14 и, по крайней мере, для некоторых из этих выпуклых конфигураций не является жёстким.
4. ЖЁСТКОСТЬ ВТОРОГО ПОРЯДКА СТРУКТУР ТЕНСЕГРИТИ.
4.1. Определение жёсткости второго порядка .
Наше определение жёсткости второго порядка для каркасов тенсегрити основано на двойном дифференцировании выражения │pj(t) — pi(t)│2 = Lij2. Это обобщает предыдущее определение жёсткости второго порядка для стержневых каркасов в [7].
Определение 4.1.1. Структура тенсегрити G(p) имеет гибкость (движения) второго порядка (p’, p"), где p' и p" — конфигурации в Rd, рассматриваемые как ассоциированная с каждой точкой pi пара векторов pi’ и pi", при выполнении следующих ограничений:
(a) Для стержней (I, j) (pi – pj)(pi’ – pj’) = 0 и |pi – pj|2+ (pi – pj)(pi’’ – pj’’) = 0.
(b) Для тросов (I, j) или (pi – pj)(pi’ – pj’) < 0, или (pi – pj)(pi’ – pj’) = 0 и |pi – pj|2+ (pi – pj)(pi’’ – pj’’) ≤ 0.
(c) Для распорок (I, j) или (pi – pj)(pi’ – pj’) > 0, или (pi – pj)(pi’ – pj’) = 0 и |pi – pj|2+ (pi – pj)(pi’’ – pj’’) ≥ 0.








