Замечание 2.2.1. Здесь основная теорема гласит, что жёсткость первого порядка каркаса тенсегрити подразумевает просто жёсткость каркаса (см. [9, 29]).
Определение 2.2.4. Изгиб первого порядка p’ является равновесным изгибом, если p’q’ = 0 для всех тривиальных изгибов первого порядка q’.
С точки зрения физики, изгиб первого порядка представляет собой векторное поле скоростей, связанное с конфигурацией (формой) структуры, при этом равновесный изгиб — это такое векторное поле, при котором линейный и угловой момент сохраняются (Рис. 5).
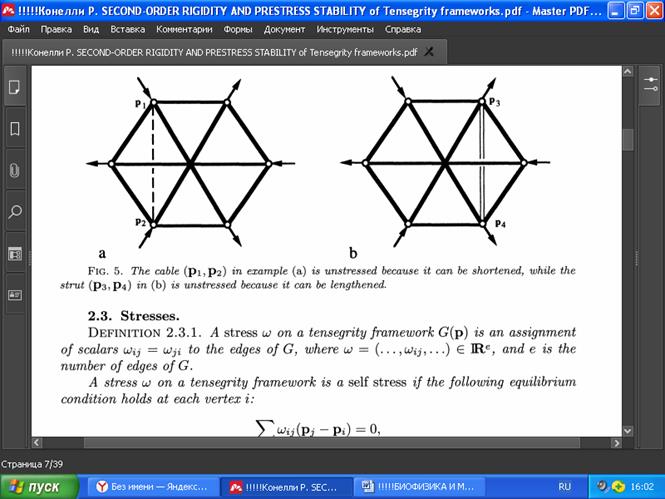
РИС . 5. Трос (p1,p2) в примере (a) не нагружен, поэтому его можно укоротить. Распорка (p3, p4) в примере (b) не нагружена, поэтому её можно удлинить.
2.3. Напряжения .
Определение 2.3.1. Напряжение w структуры тенсегрити G ( p ) задаётся в виде скаляров wij = wji на каждом ребре G (с учётом знаков), то есть вектора w = (...,wij,...) ? Re, где e — число ребер G.
Напряжение w каркаса тенсегрити является самонапряжением, если в каждой вершине (узле) i выполняются следующие условия равновесия:
∑ wij (pj - pi) = 0,
где сумма берётся по всем j при (i, j) ? E.
Собственное напряжение (самонапряжение) w называется правильным, если wij ≥ 0 для тросов (i, j) ? E_ и wij ≤ 0 для распорок (i, j) ? E+ (для стержней условия нет).
Собственное внутреннее напряжение w является строгим, если являются строгими неравенства для всех wij.
При этих обозначениях собственное напряжение (самонапряжение) w является решением системы линейных уравнений wR(p) = 0, причём w является правильным собственным напряжением, если каждое из напряжений wij тросов и распорок имеет соответствующий знак.
В [35] показано следующее.
T ЕОРЕМА 2.3.2 (тест напряжений, или стресс-тест первого порядка). Пусть G(p) — тенсегрити-каркас, где ( i , j ) - трос или распорка. Существует изгиб первого порядка p’ в G(p) такой, что
( pi – pj )( pi ’ – pj ’) # 0,
то есть трос ( pi , pj ) укорачивается или стойка ( pi , pj ) удлиняется до первого порядка тогда и только тогда, когда wij = 0 для каждого правильного собственного напряжения w в G ( p ).
Удобно изменить нынешнее представление напряжений. Пусть w = (...,wij,...) ? Re — напряжение для G(p). Определим приведённую матрицу напряжений Ω- как симметричную матрицу размером vxv с элементами:
Ωij = -wij, если I ≠ j
∑k wik, если I = j
Обозначив через pik k-ю координату точки pi ? Rd, k = 1,..., d, запишем
p1k
∑k (p1k,…, pvk) Ω- …
pvk
как квадратичную форму в vd-мерном пространстве координат всех точек (узлов, вершин) конфигурации (графа) структуры G(p). При растановке узлов (вершин) по порядку координат имеем:
p1
(p1T,…, pvT) Ω …
pv
где (…)T - операция транспонирования. Это определяет матрицу напряжений Ω, которая с точностью до перестановки координат точек р есть просто k «копий» матрицы Ω-. Легко проверить, что для р, q ? Rvd, w ? Re выполняется:
wR(p)q = pTΩq = ∑ij wij (pi - pj) (qi - qj) (1)
Таким образом, Ω есть просто матрица билинейной формы в координатах p и q такая, что w является собственным напряжением, если pTΩ = 0.
3. УСТОЙЧИВОСТЬ К ПРЕДВАРИТЕЛЬНОМУ НАПРЯЖЕНИЮ.
3.1. Энергетический принцип.
Если трос растягивается, то его энергия увеличивается. Наоборот, если укоротить распорку или длину стержня, то их энергия также увеличится. Поэтому можно объединить всех их в следующую функцию энергии (Рис. 6):
H*(q) = ∑ij fij │qj – qi│2 (2)
где
fij строго монотонно возрастает для каждого троса (i, j),
fij строго монотонно убывает для каждой распорки (i, j), (3)
fij имеющем строгий минимум в точке │pj – pi│2 для каждого стержня (i, j).
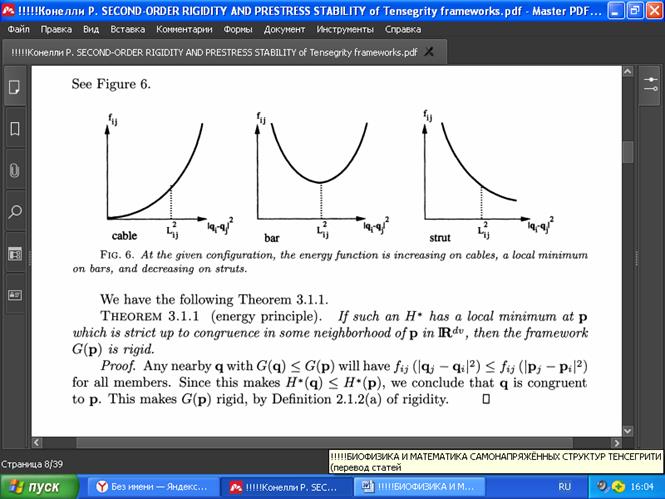
РИС . 6. Для любой формы заданной структуры функция энергии возрастает на тросах, имеет локальный минимум на стержнях и убывает на распорках.
Имеет место следующая теорема.
T ЕОРЕМА 3.1.1 (энергетический принцип). Если H * имеет локальный минимум в точке p , который является строгим с точностью до совпадения в некоторой окрестности точки p в R dv , тогда каркас G ( p ) является жёстким.
Доказательство. Для любого близкого q при G(q) ≤ G(p) будет выполняться fij (qj - qi)2 ≤ fij (pj - pi)2 для всех элементов. А поскольку тогда H*(q) ≤ H*(p), то мы заключаем, что q конгруэнтно p. Тогд G(p) - жёсткая, согласно Определению 2.1.2 (a). Теорема доказана.
Замечание 3.1.1. Оказывается, любой жёсткий каркас тенсегрити G(p) может иметь «некоторые» энергетические функции, которые делают H* минимальной в точке p. Однако, в общем случае они будут удовлетворять лишь некоторым «расслабленным» условиям (2). Поэтому в дальнейшем необходимо использовать условия (2) в их нынешнем виде.








