Определение 2.1.2. Структура тенсегрити G(p) преобладает (доминирует) над структурой тенсегрити G(q), что обозначается как G ( p ) ≥ G ( q ), если

Дата: 2025-04-30; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

|pi - pj| ≥ |qi - qj| для тросов (i, j} ? E_,

|pi - pj| = |qi - qj| для стержней {i, j} ? Eo,

|pi - pj| ≤ |qi - qj| для распорок {i,j} ? E+.

Каркас тенсегрити G(p) является жёстким в R^d, если выполнено любое из следующих трёх эквивалентных условий (см. [9] или [29]):

(а) существует число ε > 0 такое, что если G(p) ≥ G(q) и |p — q| < ε, тогда p конгруэнтно q; или

(b) если для каждого непрерывного пути, или непрерывного изгиба p(t) ? R^vd при p(0) = p выполняется G(p) ≥ G(p(t)) для всех нормированных 0 < t < 1, то есть p конгруэнтно (соответствует) p(t) для всех 0 < t < 1; или

(c) для каждого аналитического пути, или аналитического изгиба p(t) ? R^vd при p(0) = p выполняется G(p) ≥ G(p(t)) для всех нормированных 0 < t < 1, то есть p конгруэнтно (соответствует) p(t) для всех 0 < t <1.

2.2. Ж ё сткость первого порядка.

Определение 2.2.1. Изгибом (деформацией) первого порядка, или бесконечно малым изгибом каркаса тенсегрити G(p) называются такие значения координат узлов p' : V→Rⁿ, p'(vi) = pi для каждого ребра (i, j) ? Е (Рис. 4), что:

(pj – pi)(pj’ – pi’) ≤ 0 для тросов (i, j) ? E_,

(pj – pi)(pj’ – pi’) = 0 для стержней (i, j) ? E₀,

(pj – pi)(pj’ – pi’) ≥ 0 для распорок (i, j) ? E₊.

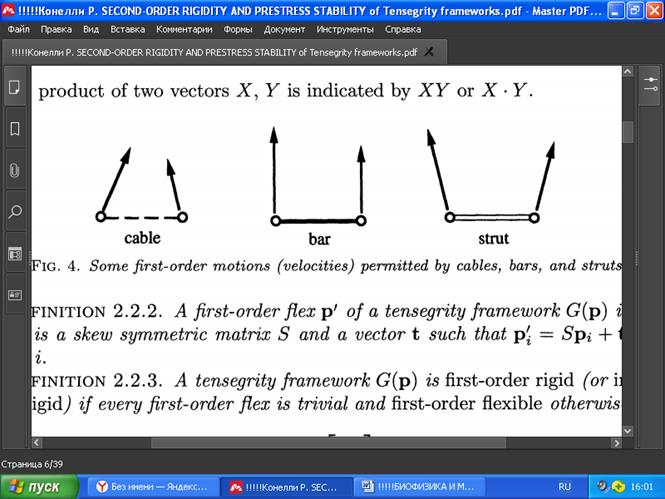
РИС. 4. Некоторые допустимые движения (скорости) первого порядка для тросов, стержней и распорок.

Определение 2.2.2. Изгиб первого порядка p' тенсегрити-каркаса G(p) тривиален, если существуют кососимметричная матрица S и вектор t такие, что pi’ = Spi + t для всех вершин (узлов) i.

Определение 2.2.3. Каркас тенсегрити G(p) является жёстким первого порядка, или имеет бесконечно малую жёсткость, если каждый изгиб первого порядка тривиален, и гибким первого порядка - в противном случае.

Удобно выражать это в терминах скалярного произведения XY или X∙Y двух векторов X и Y. Для этого зададим вектор-столбец в R^dv

p1*

p* = … ,

pv*

где каждое pi* ? R^d, i =1,...,v. И матрицу жёсткости R(p) каркаса G(p) размером exdv, определяемую формулой:

…

R(p)p* = (pj – pi)(pj* – pi*)

…

(см. [9] или [29]). Тогда изгиб первого порядка стержневого каркаса определяется решением системы линейных уравнений:

R(p)p* = 0.