В этой статье мы определяем два других класса каркасов: устойчивые к предварительному напряжению и жёсткие второго порядка.
Будем называть предварительно напряжённый (самонапряжённый) каркас (тенсегрити) устойчивым, если он имеет надлежащее строгое собственное напряжение (подробнее см. далее) такое, что некоторая функция энергии, определённая в терминах напряжения для всех конфигураций (форм) данной структуры, имеет локальный минимум при некоторой конфигурации, причём этот минимум является строгим локальным минимум вплоть до конгруэнтности всего каркаса (точную формулировку такой функции энергии см. в §3.3).
Устойчивость к предварительному напряжению — это концепция, которую мы позаимствовали из работ по проектированию конструкций. В основе определения наших энергетических функций лежит «принцип наименьшей работы»: если некоторая конфигурация (форма) каркаса соответствует локальному минимуму (по модулю жёстких движений) функции энергии, представляющей собой сумму энергий всех элементов, то ясно, что каркас является жёстким. Когда обычный тест второй производной обнаруживает такой минимум, то это соответствует устойчивости к предварительному напряжению. Пеллегрино и Калладин [28] описывают определённые условия на ранг матрицы, которые необходимы, но не достаточны для устойчивости к предварительному напряжению, поскольку их условие, по существу, игнорирует основное условие положительной определённости (см. улучшенную версию в [5]).
Заметим здесь, что для инженерных расчётов обычно задаётся соотношение между напряжением и деформацией в каждом стержне, и эта информация определяет соответствующую функцию энергии. Однако, для упрощения математической задачи распознавания (1) возможно свободно (по желанию) выбирать функции энергии элементов.
Каркас тенсегрити является жёстким второго порядка, если каждое плавное движение вершин, не нарушающее никаких ограничений на элементы по первой и второй производной, имеет тривиальную первую производную; т. е. его первая производная является производной однопараметрического семейства конгруэнтных (совпадающих) движений.

РИС. 2. Схема иерархии «жёсткостей» (цифры относятся к последующим иллюстративным примерам).
Ряд основных результатов показывает, что для любого тенсегрити-каркаса жёсткость первого порядка (т. е. бесконечно малая жёсткость) подразумевает устойчивость к предварительному напряжению, что в свою очередь подразумевает жёсткость второго порядка, что также подразумевает просто жёсткость, однако ни одно из этих следствий не может быть обратимым (см. Рис. 2, где номера рисунков относятся к примерам, приведённым далее в этой статье, и которые лежат только в соответствующей области диаграммы). Это расширяет результаты жёсткости второго порядка для стержневых каркасов в [6] и помещает устойчивость к предварительному напряжению между жёсткостями первого и второго порядков.
1.4. Стресс-тест (тест напряжений) второго порядка.
Информация о каркасах и их определённых классах может задаваться в различной форме, однако, может быть полезно связать эти различные формы с конкретной ситуацией. Например, чтобы проверить жёсткость первого порядка каркаса тенсегрити, мы можем использовать как собственные напряжения, так и изгибы первого порядка, как в стресс-тесте первого порядка.
Мы распространяем эту двойственность первого порядка на ситуацию второго порядка. Когда любое напряжение рассматривается в виде постоянных коэффициентов квадратичной формы на пространстве всех конфигураций, а также на пространстве изгибов первого порядка - это «однородная» энергетическая функция. Предположим, у нас есть фиксированная гибкость первого порядка данного каркаса, и мы хотим знать, когда эта гибкость первого порядка распространяется на какую-то гибкость второго порядка. Наш стресс-тест второго порядка утверждает следующее: изгиб второго порядка существует тогда и только тогда, когда для каждого собственного напряжения каркаса квадратичная форма, которую он определяет, неположительна при данном изгибе первого порядка. Таким образом, информация о собственных напряжениях каркаса, а также о изгибах первого порядка может предоставить информацию и о жёсткости второго порядка. Доказательство этого утверждения сводится к наблюдению того, что ограничения (ыв виде неравенств и равенств) жёсткости второго порядка и наше условие двойного напряжения являются частным случаем «альтернативы Фаркаша» (используемой в двойственности линейного программирования).
Можно уточнить (усилить) стресс-тест второго порядка, чтобы обеспечить необходимые и достаточные условия для обнаружения строгих неравенств второго порядка. Это усиление является обобщением стресс-теста первого порядка. Усиленный стресс-тест второго порядка может быть полезен не только для определения жёсткости второго порядка, но также довольно часто используется для обнаружения фактического непрерывного изгиба, при котором условия для тросов и распорок ослабляются лишь во втором порядке.
1.5. Гипотеза Рота .
В качестве приложения используемых методов проверяется гипотеза Рота о многоугольниках на плоскости из [29]. В своих «Лекциях по утерянной математике» [18, 19] Грюнбаум и Шепард предположили, что если на плоскости имеется каркас G(p) с точками в виде вершин выпуклого многоугольника со стержнями на рёбрах и кабелями внутри, соединяющими определённые пары вершин (Рис. 3а,с) таким образом, чтобы каркас был жёстким в плоскости (Рис. 1а), то затем перемена местами тросов и стержней для получения инверсной к G(p) структуры (Рис. 1b) сохраняет жёсткость (они также заметили, что исходная структура с тросами снаружи и стержнями внутри не обязательно сохраняет жёсткость, Рис. 3b,а).
Если многоугольные каркасы Грюнбаума и Шепарда жёсткие, потому что они имеют бесконечно малую жёсткость, то из этого следует, что обращённый (инверсный) каркас также имеет бесконечно малую жёсткость и, следовательно, он просто жёсткий. Гипотеза Рота заключалась в том, что все жёсткие выпуклые многоугольники с тросами внутри действительно имеют бесконечно малую жёсткость. Например, на Рис. 3с показан правильный восьмиугольник с распорками по краям и четырнадцатью тросами внутри - легко проверить, что этот каркас не обладает бесконечно малой жёсткостью. Таким образом, гипотеза Рота подразумевает, что эта структура не является жёсткой, поскольку, если бы она была таковой, то она имела бы и бесконечно малую жёсткость (читателю предлагается самостоятельно найти движение её вершин на плоскости, см. Примечание 6.2.1.)
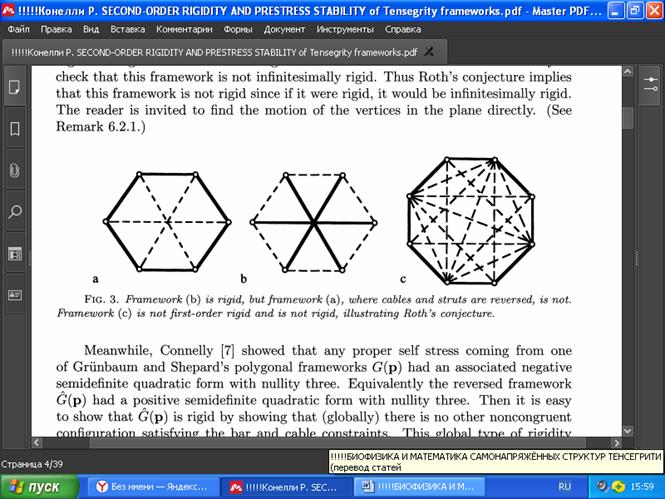
РИС. 3. Каркас (b) является жёстким, а каркас (а), в котором тросы и распорки поменялись местами - нет. Каркас (c) не является жёстким первого порядка и не является жёстким, что иллюстрирует гипотезу Рота.
Между тем, Коннелли [7] показал, что многоугольные структуры Грюнбаума и Шепарда G(p) при любом собственном внутреннем напряжении имеет связанную с ним отрицательно полуопределённую квадратичную форму с нулёвостью, равной 3. Что эквивалентно, обращённая структура G (p) имеет положительно полуопределённую квадратичную форму с нулёвостью 3. Отсюда легко показать, что G(p) является жёсткой, поскольку (глобально) не существует другой (неконгруэнтной) конфигурации, удовлетворяющей ограничениям для стерженей и тросов (знакам их напряжений). Этот глобальный тип жёсткости несколько отличается от бесконечно малой жесткости, причём они не связаны друг с другом. Однако, функции энергии, используемые для доказательства общей (глобальной) жёсткости, также подразумевают устойчивость к предварительному напряжению. Таким образом, хотя гипотеза Гринбаума была доказана и обобщена в одном направлении, однако, гипотеза Рота, являющаяся обобщением в другом направлении, не была доказана.
1.6. Доказательство гипотезы Рота.
Идея нашего доказательства гипотезы Рота состоит в следующем. Заметим, что условия строгого изгиба второго порядка в стресс-тесте второго порядка удовлетворяются для любой из структур Грюнбаума и Шепарда G(p), поскольку любое собственное напряжение определяет отрицательно полуопределённую квадратичную форму, которая является отрицательно определённой на любом пространстве нетривиальных изгибов первого порядка. Таким образом, если существует какой-либо нетривиальный изгиб первого порядка, то он распространяется на строгий изгиб второго порядка, что в свою очередь подразумевает, что будет и нетривиальный непрерывный изгиб каркаса. Таким образом, подтверждается (противоположная) гипотеза Рота: если G(p) не бесконечно жёсткая, то G(p) не является и жёсткой. В частности, если какой-либо из каркасов Грюнбаума и Шепарда G(p) является жёстким, то обращённый каркас G-(p) является одновременно бесконечно жёстким и глобально жёстким.
В приложении мы обобщим ряд «принципов замены», показывающих, когда и как можно заменять тросы или распорки на стержни и наоборот, сохраняя при этом различные уровни жёсткости или гибкости.
2. ОБЗОР СТРУКТУР ТЕНСЕГРИТИ .
В этой статье слово тенсегрити используется для определения любого каркаса структур с тросами (где каждый трос определяет максимальное расстояние между двумя точками), распорками (где каждая распорка определяет минимальное расстояние между двумя точками) и стержнями (где каждый стержень определяет фиксированное расстояние между двумя точками). Статически тросы могут только натягиваться, а распорки – работать только на сжатие. Разобьём рёбра нашего графа на три непересекающихся класса: E_ - для тросов, E0 - для стержней и E+ - для распорок, придставив тем самым граф с учётом координат и знаков элементов G = (V; E_, E0, E+). На рисунках тросы будем обозначать пунктирными линиями, распорки - двойными тонкими линиями и стержни - одинарными толстыми линиями (см. Рис. 1). Общие ссылки для этой главы: см. [8, 9, 29, 35].
2.1. Жёсткость.
Определение 2.1.1. Каркас (структура, рамка) тенсегрити G ( p ) в d -пространстве — это граф из координакт и знаков напряжений элементов (V; E_, E0, E+), где p ? Rdv такое, что каждое pi ? Rd соответствует вершине (узлу) структуры G, где p = (pi,...,pv) – сама конфигурация. Элементы в E_ — это тросы, элементы в E0 — стержни, и элементы в E+ — распорки. Каркас из стержней представляет собой каркас тенсегрити без тросов или распорок; т.е. при Е = Е0.








