Жёсткость второго порядка и Устойчивость к предварительному напряжению структур тенсегрити
Роберт Коннелли, Уолтер Уайтли
Аннотация . В этой статье определяются и описываются два понятия жёсткости самонапряжённых каркасов тенсегрити (каркасов с тросами, стержнями и распорками): устойчивость к предварительному напряжению и жёсткость второго порядка. Тем самым показано существование иерархии жёсткостей. Жёсткость первого порядка подразумевает устойчивость к предварительному напряжению, жёсткость второго порядка подразумевает жёсткость любого каркаса. Приведённые примеры показывают, что ни одно из этих следствий не является обратимым даже для стержневых каркасов. Другие примеры иллюстрируют, как эти результаты можно использовать для создания жёстких структур тенсегрити.
В статье также развивается идея двойственности жёсткости второго порядка для теста, который объединяет информацию о собственных напряжениях и изгибах каркаса первого порядка для определения жёсткости второго порядка. С помощью этого теста доказывается следующая гипотеза Рота: плоская тенсегрити-структура, в которой вершины и стержни образуют строго выпуклый многоугольник с дополнительными тросами внутри, является жёсткой тогда и только тогда, когда она является жёсткой первого порядка.
K лючевые слова: каркасы тенсегрити, жёсткие и гибкие каркасы, устойчивость каркасов, статическое напряжение, движение первого порядка, движение второго порядка.
AMS subject classifications. Primary, 52C25; Secondary, 70B15, 70C20
1. ВВЕДЕНИЕ.
Фундаментальная проблема геометрии состоит в том, чтобы определить, когда выбранные ограничения расстояний для конечного числа точек фиксируют эти точки до возможности совпадения, по крайней мере, при малых возмущениях. Мы перефразируем это как проблему жёсткости каркасов. С этой точки зрения, необходимо сделать следующее:
1) представить методы распознавания, когда данная структура является жёсткой;
2) найти способы создания жёстких самонапряжённых структур (каркасов, рам);
3) изучить взаимосвязи этих методов;
4) доказать гипотезу Рота [29] о жёсткости определённого класса плоских и пространственных каркасов.
Многие представленные здесь концепции были вдохновлены методами, используемыми при проектировании конструкций - например, принципом наименьшей работы и энергии. Однако, наша трактовка не зависит ни от каких подобных концепций, поскольку наша цель в этой статье, вообще говоря — исследовать геометрические свойства конфигураций точек в евклидовом пространстве. Тем не менее, наши результаты также проясняют и математически обосновывают некоторые методы, используемые инженерами-строителями для анализа определённых структур [5], [27], [28]. При этом наши методы расширяют уже известные [21] и дают ответы на вопросы, поставленные Тарнаи [31]. Краткое изложение полученных здесь результатов с точки зрения инженерной практики представлено в [13].
*Р.Коннелли - Факультет математики, Корнелльский университет, Итака, штат Нью-Йорк, 14853-7901 (connelly@math.cornell.edu). Работа этого автора была частично поддержана грантом Национального научного фонда MCS-790251, как выдающегося посетителя Центра математических исследований, Университета Монреаля, и программой научных премий Гумбольдта.
*У.Уайтли - Департамент математики и статистики Йоркского университета, 4700 Keele Street, North York, Ontario M3J-1P3, Канада (whiteley@mathstat.yorku.ca). Работа этого автора была частично поддержана грантами от Fonds pour la Formation de Chercheurs et I’Aide a la Recherche (Квебек) и Совета по естественным наукам и инженерным исследованиям Канады.
1.1. Используемые термины и понятия .
Каркас (структура) тенсегрити — это упорядоченный конечный набор точек в евклидовом пространстве, называемый конфигурацией (формой), с определёнными парами этих точек, называемыми тросами при условии не удаления друг от друга, с парами точек, называемыми распорками при условии их не сближения, и с парами точек, называемыми стержнями при условии сохранения расстояния между ними. Вместе распорки, тросы и стержни называются элементами (звеньями).
Если каждое непрерывное движение точек структуры, удовлетворяющее всем этим ограничениям, является ограниченным жёстким движением в объемлющем евклидовом пространстве, то мы говорим, что каркас тенсегрити является жёстким (подробнее см. [9] и [29]).
Для задачи распознавания (1) было проделано много работы с использованием концепции жёсткости первого порядка. Каркас тенсегрити является жёстким первого порядка (бесконечно жёстким), если единственное плавное движение вершин такое, что первая производная длины каждого элемента согласуется с ограничениями, имеет равную нулю производную во время ограничения конгруэнтного движения в евклидовом пространстве (подробнее об этом см. §2.2). Эквивалентная (дуальная) концепция гласит, что каркас тенсегрити является статически жёстким, если разрешена любая равновесная нагрузка (см. более подробную информацию и точное определение в [10] или [29]). Нашим рабочим определением будет определение жёсткости первого порядка, указанное выше.
Напряжение структуры тенсегрити — это наличие скалярного напряжения с учётом знака (направления) у каждого её элемента. Оно называется собственным напряжением, если в каждой вершине равна нулю векторная сумма этих скаляров (напряжений элементов с учётом знака) для соответствующих данной вершине элементов. Оно называется правильным, если напряжения в тросах неотрицательны, а напряжения в распорках - неположительны (без условия на стержнях с неизменной длиной). Он называется строгим, если напряжение отлично от нуля в каждом тросе и стойке.
1.2. Двойственность первого порядка.
Взаимодействие между движениями первого порядка и собственными напряжениями структуры даёт тест на жёсткость первого порядка. Каждый жёсткий тенсегрити-каркас первого порядка имеет строгое собственное напряжение, в соответствии с результатом Рота и Уайтли [29].
Мы формулируем стресс-тест первого порядка следующим образом: существует изгиб каркаса первого порядка, который строго изменяет длину распорки или троса тогда и только тогда, когда каждое собственное напряжение на данном элементе равно нулю.
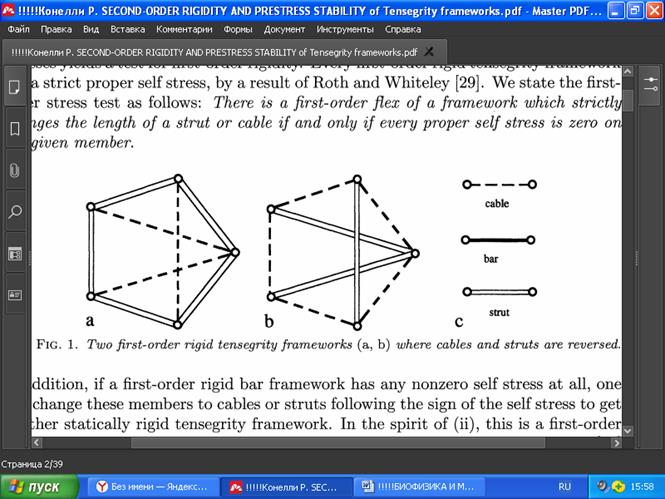
РИС. 1. Два плоских тенсегрити-каркаса с жёсткостью первого порядка, в которых тросы и распорки поменялись местами.
Более того, если жёсткий стержневой каркас первого порядка имеет какое-либо ненулевое собственное напряжение, то можно заменить эти элементы тросами или распорками, следуя лишь знаку собственного напряжения, чтобы получить другой статически жёсткий тенсегрити-каркас. Это метод первого порядка для создания примеров статически жестких каркасов тенсегрити в духе (2) (см. такие примеры в [29] и [35]). Легко заметить, что тросы и распорки любой жёсткой тенсегрити-структуры первого порядка можно поменять местами на распорки и тросы соответственно, и она останется также жёсткой первого порядка (на Рис. 1 показана такая инверсная пара плоских каркасов с бесконечно малой жёсткостью).
1.3. Устойчивость к предварительному напряжению и жёсткость второго порядка.








