C ледствие 1. Пусть G(p) - такая же, как в теореме 5, с собственным ненулевым напряжением. Тогда G(p) однозначно вкладывается в R n при n≥2 и, таким образом, G(p) - жёсткая в R n .
Доказательство. Пусть G(p’) — любая другая реализация G(p) с тросами не длиннее и распорками не короче, чем в G(p). По Теореме 5, определяющей форму энергии напряжения w для G(p), мы знаем, что E(p’) ≥ E(p) = 0. Если это неравенство строгое, то длина какой-то стойки должна уменьшиться, а какого-то троса — увеличиться. Поэтому E(p’)=E(p)=0. А поскольку E полуопределена (поскольку такова Ω), то p’ также находится в равновесии относительно ω.
Существует аффинная линейная функция T: R2→R2 такая, что Tp=p’. Можно добиться того, чтобы Tpi=pi’ для некоторых 3 неколлинеарных значений pi вектора pi. Но если это так, то и все остальные Tpi=pi’, в противном случае можно было бы добавить некоторую координату Tpi - pi’ к pi в направлении e3, не лежащим в плоскости, чтобы получить равновесное p-, не лежащее в плоскости. Но это противоречит Лемме 2, поэтому Tpi=pi' для всех i = 1,...,v .
Покажем, что T является жёстким движением в Rn. Будем предполагать, что n=2. Пусть p1,…,pv — вершины G(p), записанные в циклическом порядке по часовой стрелке, при этом будем считать G(p) строго выпуклой; то есть каждое pi находится в углу. Напомним из линейной алгебры, что T(S1) - T(0) — это эллипс с центром в начале координат, где S1 = {x E R2,│x│=1}. Те точки, где эллипс находится вне S1, соответствуют направлениям расширения T, то есть │T(x)—T(0)│ > │x│; аналогично, точки эллипса внутри S1 происходят из точек, где T сжимается, то есть │T(x)—T(0)│ < │x│ (Рис. 13).
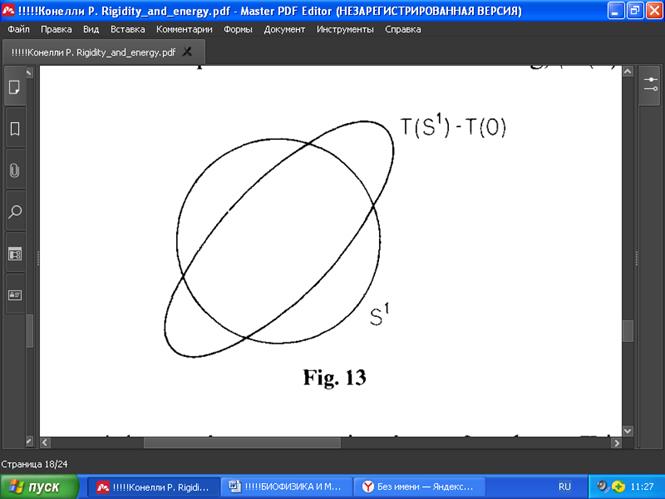
РИС. 13
Таким образом, мы имеем 4 интервала, симметричных относительно 0, где T попеременно расширяется и сжимается, или 2 интервала одного типа с 2 разделяющими их точками, или только одну область, или вовсе нет областей любого типа (нет расширения или сжатия - жёсткого движения).
Рассмотрим значения длин 0 до pi-1 - pi и pi-pi+1. Поскольку они соответствуют направлениям тросов │Tpi -Tpi+1│≤│pi - pi+1│, i=1,…,v, то эти линии должны находиться внутри или на границе сжимающихся областей. Поскольку G(p) находится в равновесии для каждого pi, то должна быть некоторая стойка pi – pj при j ≠ i-1, i+1 такая, что проходящая через 0 и pi – pj линия должна проходить между прямыми, проходящими через pi-1 - pi and pi - pi+1 по часовой стрелке. Таким образом, интервал по часовой стрелке от pi-1 - pi до pi - pi+1 должен содержать несокращающийся вектор (Рис. 14).
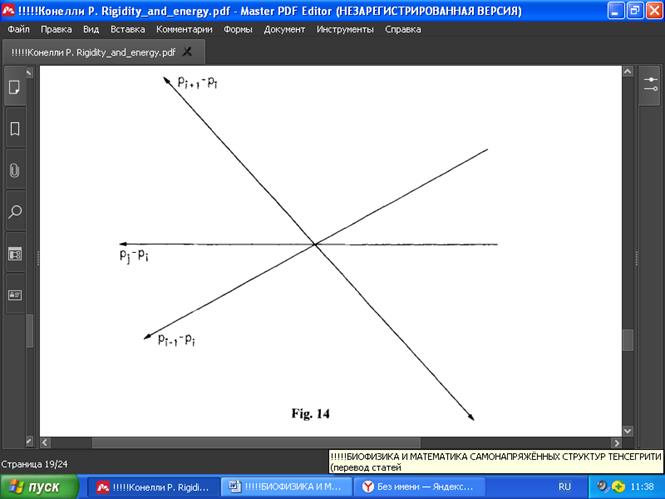
РИС . 14
Таким образом, ни один из этих интервалов по часовой стрелке не может содержаться ни в одном из сокращающихся интервалов. Но по мере того, как мы продвигаемся по выпуклому многоугольнику, каждый раз добавляя один из интервалов по часовой стрелке к следующему, мы в конечном итоге покрываем весь круг ровно один раз (разновидность касательного отображения). Но после 2 шагов мы не можем продолжать переходить от одного сжимающегося интервала к другому без перекрытия, а значит, тогда не может быть ни сжимающихся, ни расширяющихся интервалов и Т является жёстким движением. Таким образом, G(p) вкладывается однозначно, что и требовалось доказать.
Замечание 4. Следствие 1 применимо к любому многоугольному каркасу без необходимости использования Теоремы 5, если известно, что это собственное напряжение с положительной полуопределённой матрицей напряжений Ω с нулёвостью, равной 3. В частности, Следствие 1 применимо непосредственно к многоугольникам Коши с использованием Леммы 4 без необходимости использования Теоремы 5.
В следующем разделе мы покажем, как этот результат однозначного вложения многоугольников Коши может быть использован для доказательства ключевой леммы из оригинальной статьи Коши [5] и его теоремы II. Первоначальное доказательство Коши оказалось неадекватным, и с тех пор было проведено несколько заменяющих его доказательств и комментариев.
Следствие 2 ( гипотеза Грюнбаума ). Пусть G - ( p ) — структура на основе выпуклого многоугольника со стержнями на границе и тросами внутри. Пусть G — инверсная структура с тросами, заменяющими стержни в G -, и распорками, заменяющими тросы в G - . Тогда, если G - ( p ) - жёсткая в Rn , то G ( p ) однозначно вкладывается в Rn при любом n ≥2.
Доказательство. По Теореме 3, G-(p) имеет собственное ненулевое напряжение ω. Ясно, что ωij < 0 на граничных тросах. Тогда -ω — собственное ненулевое напряжение в G(p). Согласно Следствию 1, G(p) однозначно вкладывается в Rn, что и требовалось доказать.
Замечание 3. Грюнбаум и Шепард [12] отмечают, что обратное в общем случае неверно.
В трёхмерном пространстве (при n=3) должен существовать аналог Теоремы 5. Вышеприведённое доказательство, кажется, не распространяется на этот случай, однако, несколько примеров показывают, что матрица напряжений для выпуклых многогранников в R3 является полуопределённой с нулёвостью, равной 4, что и требуется. Например, к этому типу относится структура в Примере 3.
Также легко проверить, что при n=3 не могут быть разделены эллипсом 3 направления тросов и 4 направления распорок в проективной плоскости таких направлений. Таким образом, здесь применимо и Следствие 1, то есть структура однозначно вкладывается в Rn при n≥3.
Интересно отметить, что Бранко Грюнбаум привёл пример трёхмерного многогранника с тросами на границе и стойками внутри с собственным ненулевым напряжением, тросы которого образуют 3-связный граф, однако, не являющийся жёстким в R3. Однако, возможность изгиба распространяется на аффинное движение в R3, поэтому есть надежда доказать аналог Теоремы 5 и теорему о жёсткости, если имеется достаточно тросов и распорок, чтобы остановить такие нежёсткие аффинные движения. Это дало бы новую версию гипотезы Уайтли для размерности n=3 (см. Уайтли [23]).
IV . ВЗАИМОСВЯЗЬ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ.
Как упоминалось в замечании 4, для доказательства однозначности вложения многоугольников Коши могут использоваться только Лемма 4 и Следствие 1. В свою очередь, это может быть использовано для доказательства следующей леммы Коши [5] и его теоремы II.
ЛЕММА 5. Если в выпуклом плоском или сферическом многоугольнике ABCDEFG все стороны AB,BC,CD,…,FG, за исключением только AG, считать неизменными, то можно одновременно увеличивать или уменьшать углы B,C,D,E,F между этими сторонами; при этом переменная сторона AG увеличивается в первом случае и уменьшается во втором (Рис. 15).
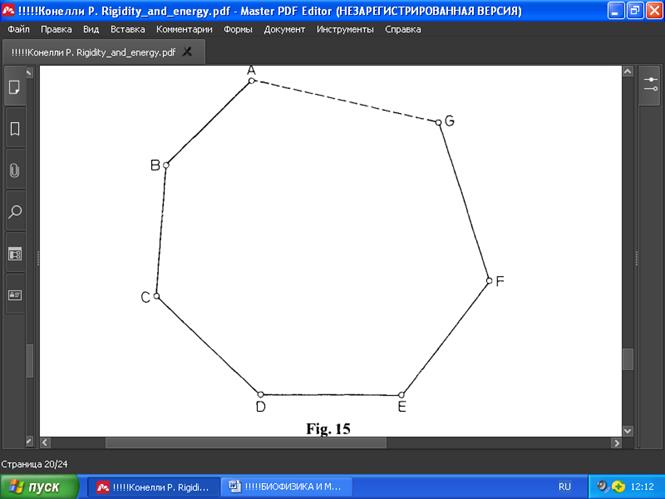
РИС.15
Здесь мы взяли на себя смелость удалить G из списка углов, которые можно одновременно увеличивать или уменьшать. По-видимому, Стейниц [20] более чем через сто лет после Коши указал, что доказательство Коши имеет некоторые пробелы. Суть проблемы заключалась в том, что по индукции, описанной Коши, многоугольник между исходным и многоугольником с разными углами может не быть выпуклым; так процесс индукции непреднамеренно прерывается (см. дальнейшие комментарии Грюнбаума и Шепарда [12] по исправлениям к статье Коши).
Конечно, доказательство Коши работает достаточно хорошо, если изменённый многоугольник «близок» к исходному. Но, естественно, этого достаточно, чтобы получить более слабое заключение о жёсткости выпуклых многогранников. Однако, позже станет ясно, что Коши имел в виду конгруэнтность любых двух «изометричных» выпуклых многогранников.
Стейниц опубликовал «правильное» доказательство леммы Коши [20], причём оно достаточно сложное. Много позже Стокер [21] дал другое доказательство весьма в духе очень естественной идеи Коши, хотя, конечно, «ловушка» Коши несколько раздражает. Люстерник [14] приводит доказательство, несколько похожее на доказательство Стейница. И совсем недавно И.Дж. Шенберг и С.К. Заремба [17] дали элегантное «простое» доказательство, включающее в себя «трюк» правильного выбора контрольной точки в середине дуги AG.
Особенно интересно сравнить лемму Коши с теоремой Акселя Шура [18] (особенно см. Черн [6], стр. 35-39). Теорема Шура — почти точный аналог леммы Коши в гладком случае; действительно, поскольку оно сформулировано для кусочно-гладкого случая, оно является обобщением леммы Коши, по крайней мере, для плоскости (n=2). Шур предполагает, что исходная дуга AG гладкая (или кусочно-гладкая), при этом изменяемая дуга имеет одинаковую длину (каждый отрезок имеет одинаковую длину), а кривизна соответствующих точек на варьируемой дуге уменьшается (как и угол между касательными, чтобы кривая по углам уменьшалась). Затем уменьшается и длина AG.
Интересно отметить, что доказательство этого у Черна [6] связано с выбором внутренней точки отсчета и оценкой некоторого интеграла. Доказательство Шенберга и Зорембы [17] почти точно такое же, как и у Черна.
Имея всё это в виду, мы безбоязненно предлагаем ещё одно - по существу, четвёртое - доказательство леммы Коши.
Доказательство Леммы 5. Поскольку преобразуются и исходный, и изменённый многоугольник, то, не теряя общности предположения, что увеличиваются все углы B, C,…, F, покажем, что AG при этом возрастает. Преимущество рассмотрения только этого случая (по крайней мере, на плоскости) состоит в том, что изменяемый многоугольник не обязан быть выпуклым и может даже не оставаться плоским, выскочив в 3-мерное или n-мерное пространство, если есть такая возможность.
Сначала рассмотрим случай, когда исходный многоугольник – плоский (n=2). Можно рассматривать стороны AB,BC,…,FG и AG как тросы, поскольку их длина не увеличивается. Поскольку углы B,…,F увеличиваются, а их стороны остаются той же длины, то длины AC,BD,…,EG также увеличиваются, поэтому их можно рассматривать как распорки. Заметим, что такой многоугольник является многоугольником Коши, поэтому, если AG убывает, то мы имеем другое вложение исходного многоугольника Коши, что невозможно. Таким образом, AG должна увеличиваться (она может оставаться неизменной только в том случае, если остаются неизменными все остальные углы и стороны).
Для сферического случая (n=3) рассмотрим конус над сферическим многоугольником, проведённый из центра сферы. Поскольку многоугольник предполагается сферически выпуклым, он лежит в полусфере, при этом существует плоская поверхность, разделяющая центр сферы и сферический многоугольник. Эта плоскость пересекает конус по плоскому многоугольнику. Если одна сторона и углы сферического многоугольника увеличены, то плоскому многоугольнику соответствует другой многоугольник с соответствующими увеличенными стороной и углами (хотя такой изменяемый многоугольник может не быть плоским, это не имеет значения, так как многоугольник Коши может изменяться и в 3-мерном пространстве). Таким образом, AG должна увеличиваться, как и прежде. Лемма доказана.
Другое приложение однозначности многоугольников Теоремы 5 относится к комментарию О. Боттема [4] о теореме Ван дер Ваардена [22]. Теорема Ван дер Ваардена гласит, что если пятиугольник с равными сторонами и равными углами между сторонами вложен в пространство, то он обязательно плоский. Впоследствии было несколько доказательств этого (например, см. С. Смакал [19]), и мы не собираемся к ним что-то добавлять. Однако О. Боттема замечает, что если такой многоугольник вкладывается в любое евклидово пространство (которое может быть и четырехмёрным) и θ — это угол между его сторонами, то 36° ≤ θ ≤ 108°. На самом деле, этим он показал, что если θ находится в этом диапазоне, то многоугольник вкладывается в 4-мерное пространство и является плоским тогда и только тогда, когда выполняется одно из сответствующих равенств. То, что θ при этом ограничено между 36° и 108°, непосредственно следует из того факта, что многоугольники Коши встраиваются однозначным образом так, что это даже позволяет им «всплывать» до 4-мерного пространства. Нижняя оценка θ следует из сравнения данного пространственного пятиугольника с плоским правильным пятиугольником, диагонали которого равны (и соответствуют) сторонам пространственного пятиугольника. Верхняя оценка θ следует из сравнения данного пространственного пятиугольника с плоским правильным пятиугольником, диагонали которого имеют ту же длину, что и (и соответствуют) диагонали пространственного пятиугольника. Ясно, что между этими значениями θ возможно много обобщений.
В [16] Рот и Уайтли замечают, что существует выпуклый многоугольный каркас G(p) со стержнями на границе (на опорах) и тросами внутри, такой, что для бесконечно жёсткой близкой к G(p) реализации G(p’) первая будет гибкой. Это даёт ответ на вопрос Грюнбаума и Шепарда в [17] на стр. 213. Используя Теорему 2 и Следствие 1, мы также можем привести несколько таких примеров. Например, такую G(p) обеспечивает любая из следующих структур Грюнбаума и Шепарда [12] или Рота и Уайтли [16]. Все вершины образуют правильный шестиугольник (Рис. 16).
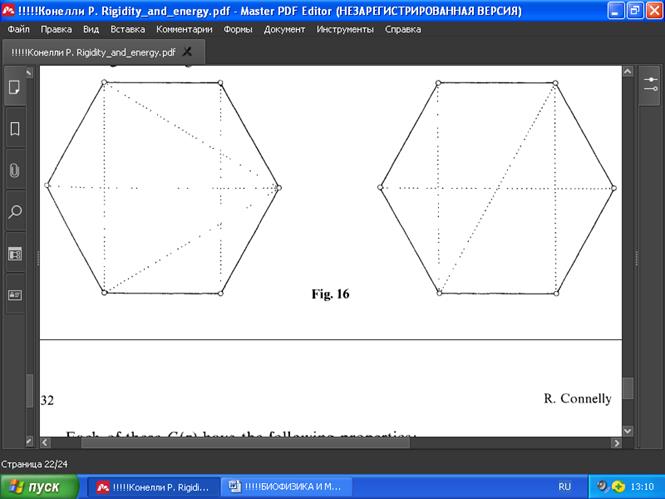
РИС . 16
Каждая из таких структур G(p) обладает следующими свойствами:
1) Если все элементы G заменить стержнями, то такая G-(p) будет бесконечно жёсткой.
2) G(p) имеет собственное ненулевое напряжение: Пусть граф G' получен инверсией (заменой) всех стержней G на тросы и всех тросов G на стержни, тогда согласно Следствию 1 G'(p) - жёсткая.
3) G(p) - гибкая (это указано для графиков на рис. 3 у Грюнбаума и Шепарда [12]).
Для любого графа (структуры) G(p), удовлетворяющего условиям (1)-(3), существует такое p', близкое к p, что G(p') - бесконечно жёсткая. Это связано с тем, что по Теореме 2, поскольку G'(p) является жёсткой (согласно (2)), то существует p' близкая к p такая, что G'(p') имеет ненулевое собственное напряжение ω на всех элементах. Но тогда -ω является собственным напряжением для G(p'). Также, согласно (1), если p' достаточно близко к p, то такая G-(p') - бесконечно жёсткая (см. Gluck [11] или Asimow и Roth [1]). Согласно основной теореме Рота и Уайтли [16], отсюда следует, что G(p') – также бесконечно жёсткая.
ИСТОЧНИКИ
1. Asimow, L., Roth, B.: The rigidity of graphs. Trans. Amer. Math. Soc. 245, 279-289 (1978).
2. Asimow, L., Roth, B.: The rigidity of graphs II. J. Math. Anal. Appi. (to appear).
3. Bolker, E.D., Roth, B.: When is a bipartite graph a rigid framework? Preprint. Univ. of Laramie.
4. Bottema, 0.: Pentagons with equal sides and equal angles. Geometriae Dedicata 2, 199-191 (1973).
5. Cauchy, A.J.: Sur les polygones et poiyédres. Second Mémoire. J. Ecole Polytechnique 19, 87-98 (1813)
6. Chern, S.S.: Studies in Global Geometry and Analysis. 4, M.A.A., 35-19 (1967).
7. Connelly, R.: The rigidity of certain cabled frameworks and the second order rigidity of arbitrarily triangulated convex surfaces. Advances in Math. 37, No. 3, 272-299 (1950).
8. Crapo, H., Whiteley, W.: Plane stresses and projected polyhedra. Preprint. of Univ. of Montreal, Jan 1977.
9. Egloff, W.: Eine Bemerkung zu Cauchy's Satz uber die Starrheit konvexes Vielflache. Abh. Math. Sem. Univ. Hamburg 20, 253-256 (1956).
10. Buckminster Fuller, R.: Synergetics, Synergetics 2. Macmillian, (1975) and (1979).
11. Gluck, H.: Almost all simply connscted closed surfaces are rigid. Geometric Topology, Lecture Notes in Math. pp. 225-239, no. 438, Berlin-Heidelherg-New York: Springer 1975.
12. Grunbaum, B., Shephard, G.C.: Lectures on lost mathematics. Mimeographed notes, Univ. of Washington, Seattle, Washington.
13. Langhaar, H.L.: Energy Methods in Applied Mechanics. Wiley 1962.
14. Lyusternik, L.A.: Convex Figures and Polyhedra. Dover, Trans. from Russian (1963).
15. Martin, H.C.: Introduction to Matrix Methods of Structural Analysis. McGraw-Hill 1966.
16. Roth, B., Whiteley, W.: Tensegrity Frameworks. Trans Amer. Math. Soc., pp. 419- 446 (1951).
17. Schoenberg, I.J., Zaremba, S.K.: On Cauchy’s Lemma Concerning Convex Polygons. Canad. J. of Math. 19, 1062-1071 (1967).
18. Schur, A.: Uber die Schwarzche Extremaleigenschaft des Kreises unter den Kurven konstantes. Krummung. Math. Ann. 83, 143-148 (1921).
19. Smakal, S.: Regular Polygons. Czechoslovak Math. J. 28, (103) no. 3, 373-393 (1978).
20. Steinitz, E., Rademacher, H.: Vorlesunger uber die Theorie der polyeder. Berlin-Heidelberg-New York: Springer (1934).
21. Stoker, J.J.: Geometrical Problems Concerning Polyhedra in the Large. Com. Pure and App. Math. Vol. XX1, 119-168 (1968).
22. Van der Waerden, B.L.: Ein Satz uber raumliche Funfecke. Elem. Math. 25, 73-78 (1970).
23. Whiteley, W.: Conjectures on rigid Frameworks, letter for A.M.S. special session on rigidity in Washington. D.C., October 1979.
24. Whiteley, W.: Adress at the special A.M.S. session on rigidity in Syracuse. Dec. 1978.
Написано в период 20. XI .1980 – 02. X .1981
SIAM J. DISCRETE MATH.
© 1996 Society for Industrial and Applied Mathematics 008
Vol. 9, No. 3, pp. 453-491, August 1996
Поступило в редакцию 13 апреля 1992 г.
Принята к печати (в переработанном виде) 10 октября 1995 г.








