Задание 6. Интегрирование тригонометрических выражений.
Пусть 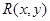 — рациональная функция своих аргументов.
— рациональная функция своих аргументов.
1) Интегралы вида 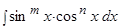 , где m и n - целые числа.
, где m и n - целые числа.
Рассмотрим два случая:
а) Среди чисел m, n есть хотя бы одно нечетное. Тогда отделяем от нечетной степени один сомножитель и выражаем с помощью формулы 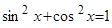 оставшуюся функцию в четной степени. Вводим новую переменную и приходим к табличному интегралу.
оставшуюся функцию в четной степени. Вводим новую переменную и приходим к табличному интегралу.
Пример. 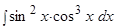 .
.
Решение.
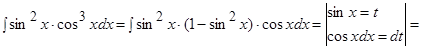
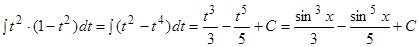 .
.
б) Оба числа m, n- четные неотрицательные.
Применим формулы:
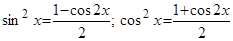 .
.
Пример. 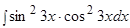 .
.
Решение.
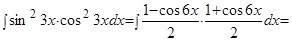
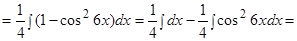
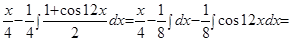
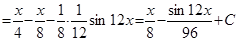 .
.
2) Интегралы вида 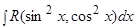 , где
, где 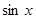 и
и 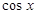 входят в подынтегральную рациональную функцию, только в четных степенях.
входят в подынтегральную рациональную функцию, только в четных степенях.
Делается замена: 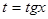 .
.
При этом 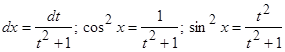 .
.
Пример. 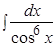 .
.
Решение.
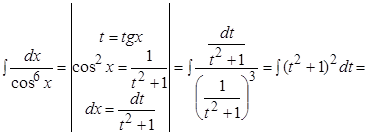
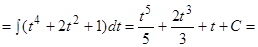
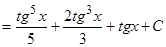 .
.
3) Интегралы вида 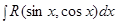 , где
, где 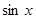 и
и 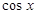 входят в подынтегральную рациональную функцию в нечетных степенях.
входят в подынтегральную рациональную функцию в нечетных степенях.
Делается универсальная тригонометрическая подстановка: 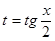 . В результате сводится к интегралу от рациональной дроби.
. В результате сводится к интегралу от рациональной дроби.
При этом 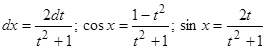 .
.
Пример. 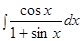 .
.
Решение.
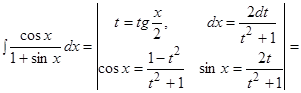
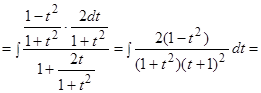
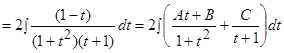 .
.
Приводим к общему знаменателю подынтегральную функцию. А поскольку дроби равны и их знаменатели равны, то равны и числители:
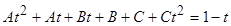 .
.
Два многочлена равны, когда равны коэффициенты при соответствующих степенях:
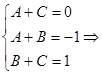
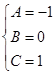 .
.
Получаем:
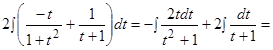
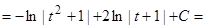
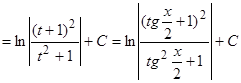 .
.
Задание 7. Интегрирование иррациональных выражений.
Рассмотрим некоторые типы интегралов, которые надлежащей подстановкой могут быть сведены к интегралам от рациональных функций, а, следовательно, могут быть выражены через элементарные функции. Пусть R(u) — рациональная функция переменной u. Возможны несколько случаев.
1) Интегралы вида: 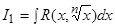 и
и 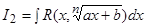 , где
, где 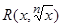 и
и 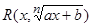 – рациональные функции от
– рациональные функции от 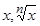 и
и 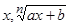 , соответственно, а
, соответственно, а 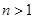 — натуральное число.
— натуральное число.
С помощью подстановок 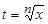 и
и 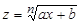 указанные интегралы сводятся к интегрированию рациональных функций от t и z, соответственно.
указанные интегралы сводятся к интегрированию рациональных функций от t и z, соответственно.
Пример. 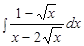 .
.
Решение. Сделаем замену 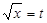 , откуда
, откуда 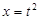 ,
, 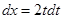 . В результате получим:
. В результате получим:
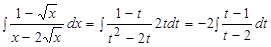 .
.
Исходный интеграл сведен к интегралу от рациональной функции – неправильной дроби, которую интегрируем с помощью выделения ее целой части:
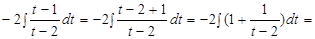
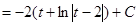 .
.
Таким образом, 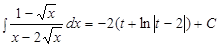 , где
, где 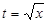 .
.
Пример. 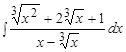 .
.
Решение.
Полагая 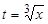 , имеем
, имеем 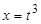 ,
, 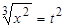 ,
, 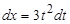 .
.
Откуда:
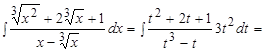
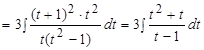 .
.
Таким образом, мы пришли к интегралу от рациональной функции переменной t, представленной неправильной дробью. Интегрируем ее методом выделения целой части:
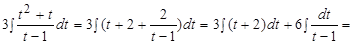
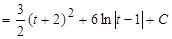 .
.
Таким образом, 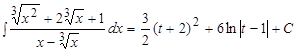 , где
, где 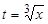 .
.
Пример. 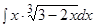 .
.
Решение. Сделаем замену 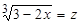 , откуда
, откуда 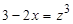 ,
, 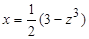 ,
, 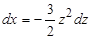 .
.
Имеем:
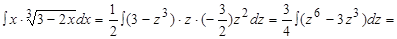
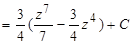 , где
, где 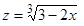 .
.
2) Если в подынтегральную функцию входят радикалы с разными показателями вида 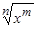 ,
, 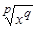 и т.д. или
и т.д. или 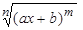 ,
, 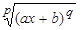 и т.д.
и т.д.
Сводим к интегрированию рациональных функций от переменных tи z с помощью подстановок 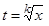 и
и 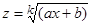 соответственно, где k - наименьшее общее кратное показателей корней, т.е. чисел n, p, …
соответственно, где k - наименьшее общее кратное показателей корней, т.е. чисел n, p, …
Пример. 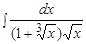 .
.
Решение. Показатели радикалов подынтегральной функции равны 2 и 3. Их наименьшее общее кратное (наименьшее число, которое делится на 2 и на 3) равно 6. Поэтому произведем замену переменной 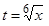 . Тогда
. Тогда 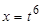 ,
, 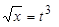 ,
, 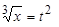 ,
, 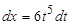 .
.
Следовательно,
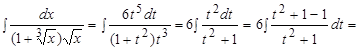
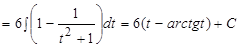 , где
, где 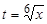 .
.
Пример. 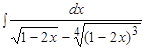 .
.
Решение. Показатели радикалов подынтегральной функции равны 2 и 4. 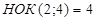 . Поэтому производим замену переменной
. Поэтому производим замену переменной 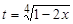 . Тогда
. Тогда 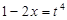 ,
, 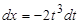 .
.
Следовательно,
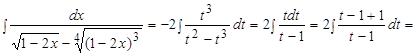
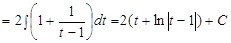 , где
, где 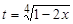 .
.
3) Интеграла вида 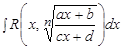 .
.
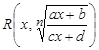 — рациональная функция от
— рациональная функция от 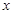 и
и 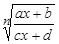 ,
, 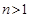 - натуральное число и выполнено неравенство
- натуральное число и выполнено неравенство 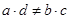 .
.
С помощью замены переменной 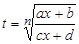 нахождение такого интеграла сводится к интегрированию рациональной функции от t .
нахождение такого интеграла сводится к интегрированию рациональной функции от t .
Пример. 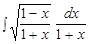 .
.
Решение. Положим 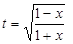 , откуда
, откуда 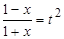 ,
, 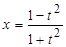 ,
, 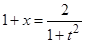 ,
, 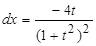 .
.
Следовательно,
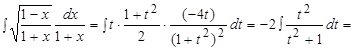
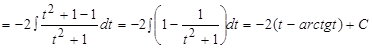 ,
,
где 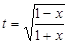 .
.
Пример. 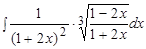 .
.
Решение. Полагая 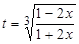 , имеем
, имеем 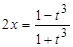 ,
, 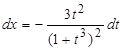 ,
, 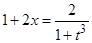 .
.
Тогда
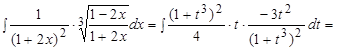
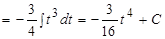 , где
, где 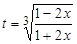 .
.
4) Тригонометрические подстановки.
Интегралы 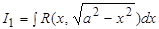 ,
, 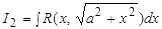 ,
, 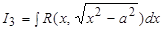 приводятся к интегралам от рациональных функций относительно
приводятся к интегралам от рациональных функций относительно 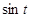 и
и 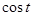 с помощью следующих тригонометрических подстановок:
с помощью следующих тригонометрических подстановок:
для интеграла 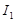 :
: 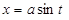 ;
;
для интеграла 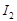 :
: 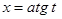 ;
;
для интеграла 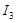 :
: 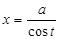 .
.
Пример. 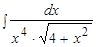 .
.
Решение. Это интеграл второго типа. Поэтому применим подстановку 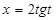 .
.
Тогда 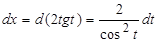 .
.
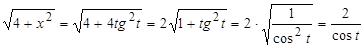 .
.
Следовательно,
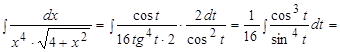
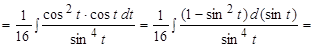
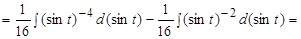
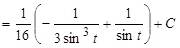 , где
, где 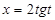 .
.
Пример . 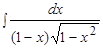 .
.
Решение. Этот интеграл первого типа и поэтому применим подстановку 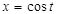 .
.
Тогда 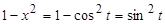 ,
, 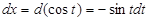 .
.
Следовательно,
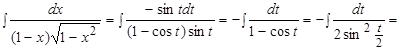
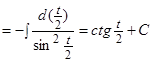 , где
, где 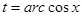 .
.
1. Определенный интеграл и его приложения
Если 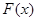 — некоторая первообразная функции
— некоторая первообразная функции 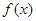 , непрерывной на отрезке
, непрерывной на отрезке 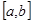 , то определенный интеграл вычисляется по формуле Ньютона – Лейбница:
, то определенный интеграл вычисляется по формуле Ньютона – Лейбница:
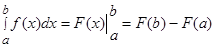 .
.
Пример. 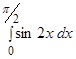 .
.
Решение.
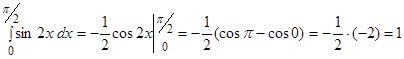 .
.








