ЛЕММА 4. Любой многоугольник Коши G(p) имеет ненулевое собственное напряжение с положительно полуопределённой матрицей напряжений и нулёвостью, равной 3.
Доказательство. Используем индукцию по v - количеству вершин G. Начнём с v=4. Пример 2 является многоугольником Коши, а по свойству D все многоугольники Коши с v=4 удовлетворяют утверждению этой леммы. Тогда все многоугольники Коши с v или меньшим числом вершин имеют положительно полуопределённую матрицу напряжений с нулёвостью, равной 3. Покажем, что это же справедливо для v+1 вершин, а значит, и большего их числа (по индукции).
Используем тот факт, что
w"v+1,v-2 Ω’ – w’v+1,v-2 Ω" = Ω
есть матрица напряжений для G(p) (Рис. 11). Пусть G(p)=G(p1,…,pv+1) — заданный многоугольник Коши с v+1 вершиной. Пусть G'(p1,…,pv-1,pv+1) — многоугольник Коши с теми же вершинами при удалённой вершине pv. Пусть G"(pv-2,pv-1,pv,pv+1) — многоугольник Коши из «последних» четырёх вершин G, начиная с v-2. Пусть Ω' и Ω" — положительно полуопределённые матрицы напряжений с нулёвостью 3 соответственно структур G'(p1,…,pv-1,pv+1) и G"( pv-2,pv-1,pv,pv+1).
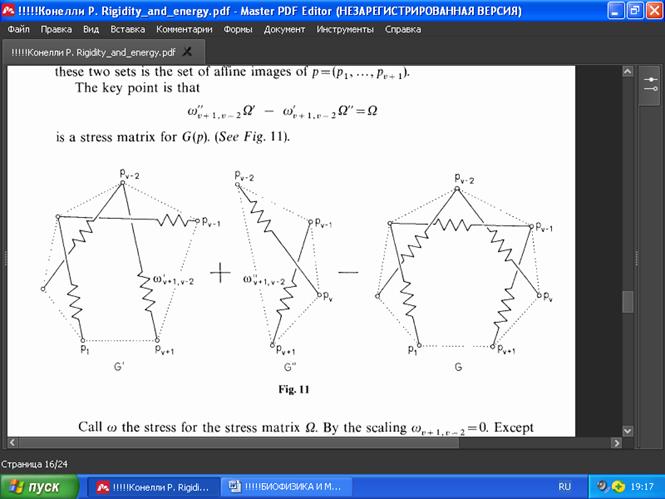
РИС. 11
Пусть G-’ - граф, полученный добавлением одной вершины v и без рёбер в G'. Пусть Ω-’ - симметричная матрица размером (v+1)x(v+1) структуры G-'(p-), где p-=(p1,…,pv-1,pv, pv+1} с произвольным значением pv. Можно утверждать, что G-'(p-) имеет «то же» напряжение, что и G'(p1,…, pv-1,pv), так как Ω-' получена просто добавлением к Ω' строки и столбца нулей (нулевых напряжений).
Аналогичным образом определим Ω-" как симметричную матрицу размером (v+1)x(v+1), полученную добавлением v-3 строк и столбцов нулей к Ω". Заметим, что в Ω-" значение напряжения w"v+1,v-2 > 0, а в Ω-' значение напряжения w'v+1,v-2 < 0 (напомним, что внедиагональные элементы матрицы равны этим напряжениям со знаком минус).
Из доказательства Леммы 2 видно, что нулевое пространство Ω-’ естественным образом отождествляется с множеством аффинных образов (p1,…,pv-1,pv-’,pv+1) при v-й произвольно выбранной вершине pv-’. С другой стороны, нулевое пространство Ω-" можно отождествить с аффинными образами (p1-",…,pv-3-",pv-2,pv-1,pv,pv+1) при первых v-3 произвольно выбранных вершинах. Ясно, что пересечение этих двух множеств есть множество аффинных образов p = (p1,…,pv+1).
Пусть ω – напряжения в матрице напряжений Ω. Положим ωv+1,v-2 = 0. Все остальные напряжения являются суммой напряжений одного знака, за исключением напряжения wv+1,v-1. При этом заметим, что
wv-1,v = -w’v+1,v-2w"v-1,v > 0
wv,v+1 = -w’v+1,v-2w"v,v+1 > 0
Если wv,v-2 ≥ 0, то, поскольку конечный многоугольник G(p) выпукл в pv, G(p) не может
находиться в равновесии при значении pv. (См. лемму 6.2 Рота и Уайтли [16].) Таким образом, wv,v-2 < 0 и Ω является матрицей напряжений (с собственным напряжением) для многоугольника Коши G(p).
Так как каждая из Ω-’ и Ω-" положительно полуопределена, то же справедливо и для Ω. Таким образом, нулевое пространство Ω есть пересечение нуль-пространств Ω-' и Ω-", и оно отождествляется с множеством аффинных изображений p, согласно приведённым выше аргументам. Таким образом, Ω имеет значение нулёвости, равное 3. Лемма доказана.
Можно показать, что многие частные случаи плоских многоугольных структур имеют такие же матрицы напряжений. Однако, с большим классом можно иметь дело, только если известно, что для данного p существует некоторая матрица Ω с большим количеством отличных от нуля элементов, чем требуется, которая имеет требуемую нулёвость и определённость. Для этого докажем следующую теорему.
T ЕОРЕМА 5. Пусть G(p) — плоская структура, где p — выпуклый многоугольник с тросами по границе и распорками внутри. Пусть G(p) имеет собственное ненулевое напряжение ω. Тогда матрица напряжений Ω для ω имеет нулёвость 3 и является положительно полуопределённой.
Доказательство . Сначала покажем, что нулевое значение Ω в точности равно 3. По Лемме 2, нулевое значение не меньше 3. Если оно больше 3, то в R3 существует G(p-) с напряжением ω, которая ортогонально проектируется на G(p) в R2, при этом аффинная оболочка G(p-) трёхмерна.
Пусть H — выпуклая оболочка вершин G(p-) в R3. Каждая естественная грань, или грань H - двумерное пересечение H с опорной плоскостью - однозначно проецируется в R2. Достаточно рассмотреть только верхние грани H, то есть грани, видимые из +∞. Это предполагает разложение выпуклого многоугольника в R2 как выпуклой сетевой структуры. Но поскольку H трёхмерен, то внутри многоугольника будет некоторое ребро e, которое является проекцией верхнего ребра e- многоугольника H, при этом многоугольник разделяет одномерная грань H. Значит, G(p) должна пересекать некоторая стойка e, чтобы было возможно равновесное напряжение w, поскольку, если бы не было такой стойки, её можно было бы значительно увеличить, сохранив все тросы фиксированной длины и увеличив любую другую возможную длину стойки. Но это изменит (уменьшит) энергию таким образом, что даже первая производная будет меньше 0, а это невозможно в критической точке, т. е. при нахождении G(p) в равновесии. Таким образом, G(p) должна пересекать внутри некоторая стойка e.
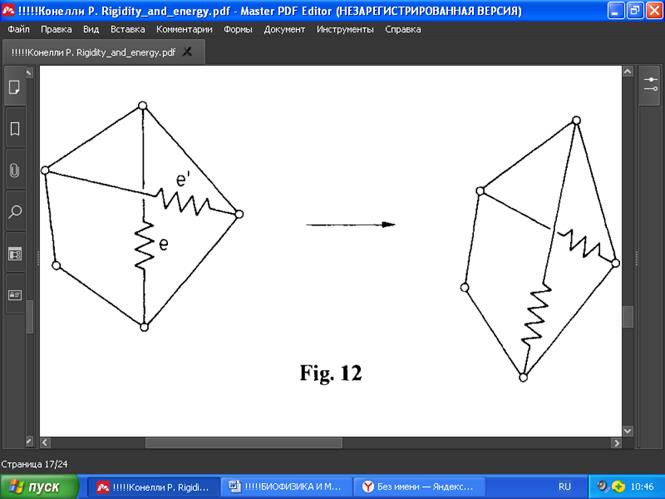
РИС . 12
Пусть e’ — распорка G(p), пересекающая рабро e (Рис. 12). Пусть e-' - соответствующая стойка в G(p-). Заметим, что ни одна из конечных точек e-’ не является одной из конечных точек e-. e разделяет вершины G на два множества V1 и V2, при этом концы e соответствуют пересечению множеств V1∩V2.
Будем считать G(p-) «шарнирно закрепленной» вдоль e- и рассмотрим движение G(p-), которое просто сглаживает этот шарнир, перемещая каждое V1 и V2 как жёсткое множество. Заметим, что это увеличивает длину e-’ и любой другой такой поперечной стойки даже так, что их первые производные больше 0. Таким образом, первая производная энергии структуры G в точке p- отрицательна, а это невозможно, как уже упоминалось ранее, если G(p) находится в равновесии при напряжении ω. (Эффект этих движений состоит в том, чтобы выровнять каркас G(p-) в плоскости так, чтобы всякий раз уменьшить энергию.) Таким образом, нулёвость Ω точно равна 3, согласно Лемме 2.
Осталось показать, что матрица Ω положительно полуопределена. Пусть Ω(1) — матрица напряжений для многоугольника Коши с вершинами p. Рассмотрим матрицу напряжений Ω(t) = (1—t)Ω + tΩ(1), 0 ≤ t ≤ 1. Согласно вышеизложенному, каждое Ω имеет значение нулёвости, равное 3, поскольку это матрица напряжений с требуемым напряжением ω (позволяющим любому внутреннему элементу, как распорке, иметь отрицательное напряжение). Согласно Лемме 4, Ω(1) положительно полуопределена. Согласно сказанному выше, Ω(t) имеет нулёвость 3 для всех 0 ≤ t ≤ 1. По Лемме 3, Ω(0) = Ω также положительно полуопределена. Теорема доказана.
Уолтер Уайтли предположил следующее.








