III . Квадратичные энергетические функции
Мы уже видели, как энергетические функции использовались для нахождения напряжений в Теореме 2. Теперь используем напряжения для создания общей функции энергии. Оказывается, во многих случаях энергия имеет минимумы, которые достаточно просто описать в полном виде. Затем мы это используем, чтобы показать, что каркас является жёстким, поскольку нежёсткие движения, сохраняющие минимальную энергию, не являются допустимыми изгибами для каркаса.
Для знакомства с энергетическим методом рассмотрим сначала очень простой случай. Предположим, что G(p) — каркас, в котором подмножество вершин B
зафиксировано (неподвижно), а остальные вершины могут свободно перемещаться. При этом «за кулисами» (вне рассмотрения) предполагается некоторый жёсткий каркас, включающий в себя вершины B, а все (остальные) рёбра G являются тросами. Каждая вершина G, не принадлежащая B, также соединена с B последовательностью тросов. Используя соответствующую квадратичную функцию энергии, легко доказать следующую теорему.
T ЕОРЕМА 4. Пусть вершины B удерживаются неподвижно. Пусть ω - напряжения в G ( p ) с каждым значением ωij > 0, где мы требуем равновесия только в вершинах G , не принадлежащих B . Тогда G ( p ) - жёсткая.
Доказательство. Пусть энергия структуры G(q) равна:
E(q) = 1/2 ∑ ωij ( qi - qj )2
где сумма берётся только по тросам в G(p) и q E Rnv. E является квадратичной
функцией, вершины B в которой представлены как константы. Заметим, что VE(q) - градиент E в точке q - является аффинной линейной функцией q:
VE ( q ) = (…, ∑ωij ( qi - qj ),…)
Покажем, что E имеет единственный минимум в точке p. Если q — любая точка, отличная от p, то E ((1- t ) p + tq ) — квадратичный полином от t, стремящийся к бесконечности при t стремящемся к бесконечности, и производная которого при t=0 равна:
VE(p)(q - p) = 0.
VE(p)=0 по условию равновесия для ω. Если некоторая вершина G(p) (не принадлежащая B) отлична от соответствующей вершины G(q), то она будет перемещаться в бесконечность соответственно выражению (1-t)p+tq при t→±∞. Так как каждая вершина соединена с вершиной B последовательностью тросов, то при больших t некоторые тросы должны стать сколь угодно длинными. А поскольку все ωij > 0, это означает, что значение E также должно стать большим. Таким образом, p — единственный минимум E.
Тогда G(p) - жёсткая, поскольку если G(q) — любая другая возможная реализация и │qi - qj│≤│pi - pj│для каждого троса (i, j), то E(q) ≤ E(p). Поэтому p является единственным минимумом p=q, что и требовалось. Теорема доказана.
Замечание 3. Теорему 4 можно исппользовать для объяснения жёсткости паутины.
Её тонкие нити прикрепляются к какому-то твёрдому предмету, а затем она
растягивается до тех пор, пока не будет достигнуто требуемое напряжение (Рис. 4).
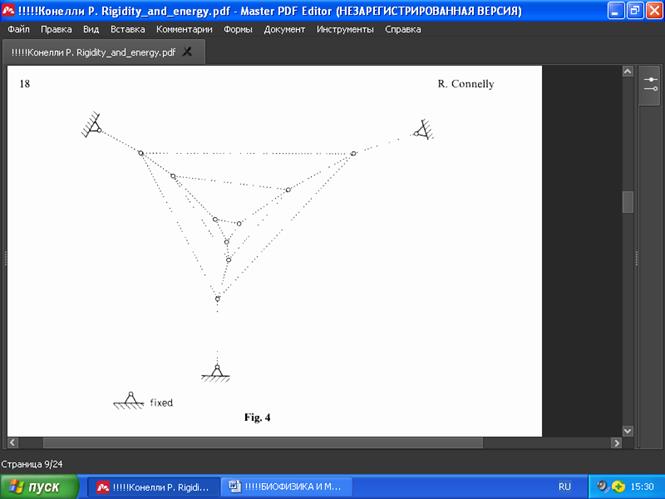
РИС . 4
В самом деле, если такой каркас является жёстким, то можно считать, что вершины B удерживаются в жёстком состоянии некоторым бесконечно жёстким стержневым каркасом G1(p) с минимальным числом стержней. Затем вершины паутины присоединяются тросами к G1(p), чтобы получить G2(p), содержащую в себе G1(p). Сама по себе G1(p) не может иметь предварительных напряжений (см., например, статьи Глюка [11] или Азимова и Рота [1]). Некоторые из тросов G2(p), соединённых с B, будут иметь ненулевое собственное напряжение, согласно Теореме 3 для жёсткой структуры. Если это не все вершины G2(p), то можно включить в B новые вершины и повторить приведённое выше рассуждение – тогда, в конце концов, все вершины будут включены в G2(p). Таким образом, все формы каркаса, для которого может применяться Теорема 4 (возможно, без положительного напряжения), если они жёсткие, являются жёсткими и в случае нескольких применений Теоремы 4. Это также связано с жёсткостью стержневых каркасов более высокого порядка, обсуждаемой Коннелли в [7].
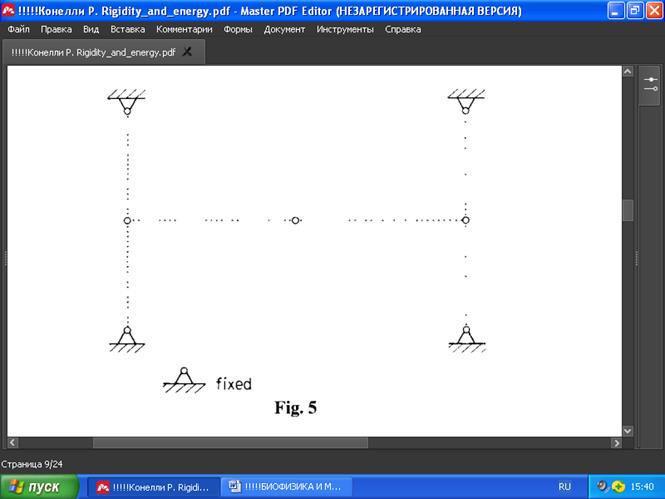
РИС. 5
Например, стержневой или тросовый каркас на Рис. 5 является жёстким в двух приложениях Теоремы 4, и как стержневой каркас, казалось бы, будет жёстким «третьего порядка».
Рассмотрим более общий тип энергетической функции. Пусть ω E Re — собственное напряжение для G(p), тогда для q E Rnv
E(q) = 1/2 ∑ ωij ( qi - qj )2
будем называть формой энергии, связанной с напряжением w для G(p). В отличие от ранее изложенного, когда некоторые вершины считались неподвижными (константами), теперь E(q) является однородной квадратичной функцией nv переменных. Рассмотрим некоторые её свойства:
A. VE(p) = 0 (это просто утверждение, что w является напряжением для G(p)).
B. VE(q) – линейная функция q (поскольку E(q) — квадратичная функция).
C. E(p) = 0. Предположим, что E(p) ≠ 0, тогда функция E(tp) = t2*E(p) – непостоянна, где t – действительное число; но dE(tp)/dt = VE(tp)*p = 0 согласно свойству B, то есть E(tp) – постоянна. Таким образом, мы получили противоречие, то есть Е(р)=0.
D. Множество нулей VE, то есть критические точки E инвариантны относительно аффинных линейных преобразований, т.е. если преобразование T: Rn→Rn – аффинное линейное, определяемое как T(p)=(Tp1,…, Tpv), то E(T(p)) = 0 и VE(T(p)) = 0. Рассмотрим аффинно-линейную функцию T: Rn→Rn, то есть Tx = Lx + b, где L - линейна, а b - постоянный вектор. Тогда
VE(Tp) = (…,∑ωij (Tpi -Tpj),…) = (…,∑ωij (Lpi - Lpj),…) = (…,L ∑ωij (pi - pj),…) = 0.
Таким образом, ω является напряжением как для p, так и для Tp = (Tp1,...,Tpv), поскольку E(Tp) = 0.
Чтобы подробнее рассмотреть свойства энергетической функции E, нужно немного сконцентрироваться. Хотя E(q) является квадратичной функцией nv переменных, соответствующая ей матрица E имеет определённую избыточность. Прежде обратим внимание, что
ωij (pi - pj)2 = ωij pi2 + ωij pj2 - 2ωij pi pj
Зададим симметричную матрицу Ω, (i, j)-й элемент которой равен —wij при i≠j, а k∑wik = k∑wkj, если i=j, поскольку wij=wji. Мы будем называть Ω матрицей напряжений, ассоциированной с напряжением w =(…,wij,…) E Re. Заметим, что если бы мы рассматривали pi как формальные символы, то матрицей E была бы 1/2 Ω, что не следует путать с матрицей Ω у Болкера и Рота [3]. Однако, надо уточнить, что если Q — квадратичная форма, ассоциированная с Ω, такая, что Q(x) = x’Qx (где x’ - транспонирование x) для x E Rv, то
E(q) = n∑Q(pek),
где e-I = (ei,…,ei), i=1,…,n, ei — стандартный i-й базисный вектор (с i-й координатой
v раз
равной 1 и остальными равными 0) в R n. Тогда матрица E — это всего лишь «n копий» Ω, и в дальнейшем можно использовать последнюю.
Примечание. E является положительно полуопределённой тогда и только тогда, когда таковой является Ω. Однако, Ω никогда не бывает определена и имеет не менее одного нулевых значений, поскольку (1,…,1) всегда находится в нулевом пространстве (нуль-пространстве) Ω. Сумма строк и столбцов Ω всегда равна 0, что следует из её определения.
ПРИМЕР 1. Рассмотрим структуру G(p), где p1, p2, p3, p4 — вершины квадрата на плоскости, причём внешние края — это тросы, а две диагонали — распорки. Равновесными для G(p) являются напряжения +1 на тросах и -1 на стойках (Рис. 6).
Соответствующая матрица напряжений для этого случая:
1 -1 1 -1
Ω = -1 1 -1 1
1 -1 1 -1
-1 1 -1 1
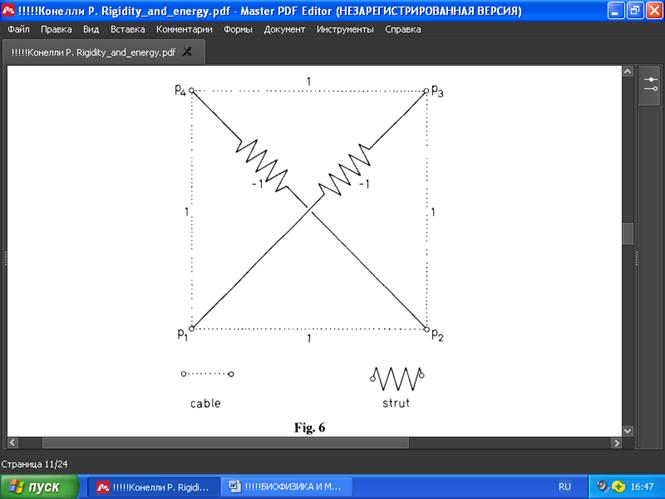
РИС. 6
Эта Ω является положительно полуопределённой с нулевым пространством («нулёвостью») размерностью 3. Напомним, чтобы матрица была полуопределённой, достаточно найти vn переменных и показать, что подматрицы kxk, k ≤ vn, полученные с использованием первых (или последних) k из nv переменных, имеют положительные определители, при этом определитель n - нулевой. Поскольку здесь диагональные элементы положительны, то Ω - полуопределена. Важность этого будет раскрыта позже.
ПРИМЕР 2. Это обобщение предыдущего примера, где четыре вершины G(p) расположены более широко. Мы можем изменять положения p с помощью аффинных линейных преобразований, не изменяя при этом напряжение ω. Здесь можно считать, что три из четырёх точек находятся в особом положении - соответственно, принимем p1 = (0, 0), p2 = (1, 0), p3 = (a, b), p4 = (0, 1). Чтобы при этом G(p) представляла собой выпуклый многоугольник, должно выполняться ограничение a + b > 1 (рис. 7).
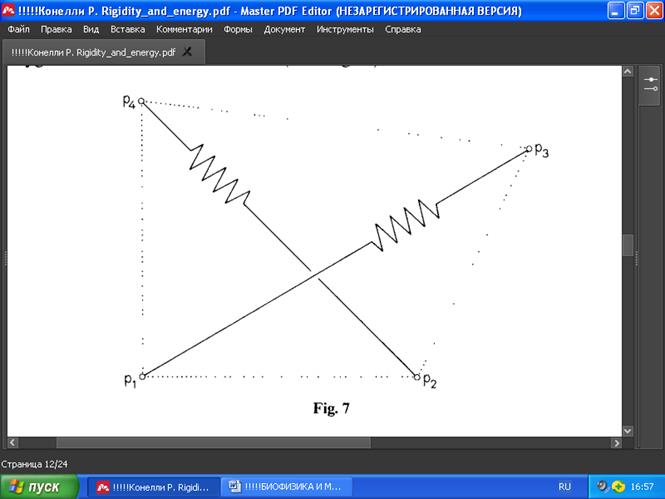
РИС . 7
Поскольку напряжения определяются с точностью до постоянного коэффициента, будем считать ω13 = 1. Тогда уравнения равновесия дают следующую матрицу напряжений:
p1 p2 p3 p4
p1 a+b-1 -a 1 -b
p2 -a a2/(a+b-1) -a/(a+b-1) ab/(a+b-1) = Ω
p3 1 -a/(a+b-1) 1/(a+b-1) -b/(a+b-1)
p4 -b ab/(a+b-1) -b/(a+b-1) b2/(a+b-1)
Обратите внимание, что два диагональных напряжения w13, w24 всегда отрицательны, боковые напряжения - положительны, а Ω является положительно полуопределённой с нуль-пространством размерностью 3.
ПРИМЕР 3. Пусть вершины G(p) — углы единичного куба в R3 с тросами по краям и распорками по 4-м диагоналям (рис. 8).
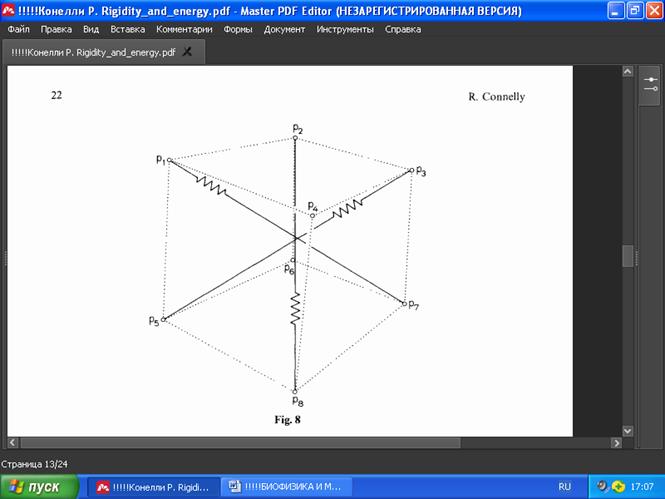
РИС. 8
Тогда, если напряжения тросов равны +1, а напряжения распорок равны -1, то матрица напряжений будет равна:
p 1 p 2 p 3 p 4 p 5 p 6 p 7 p 8
p1 2 -1 0 -1 -1 0 1 0
p2 -1 2 -1 0 0 -1 0 1
p 3 0 -1 2 -1 1 0 -1 0
p 4 -1 0 -1 2 0 1 0 -1 = Ω
p 5 -1 0 1 0 2 -1 0 -1
p 6 0 -1 0 1 -1 2 -1 0
p 7 1 0 -1 0 0 -1 2 -1
p 8 0 1 0 -1 -1 0 -1 -2
Эта матрица имеет нуль-пространство размерностью 4 и является положительно полуопределённой.
Матрица напряжений лишь отдалённо связана с матрицей 3vx3v, используемой инженерами-строителями и называемой матрицей жёсткости (см., например, Мартин [15] или Лангхаар [13]). Наша матрица напряжений (или, скорее, её энергетическая матрица) предполагает, что все элементы являются идеально упругими пружинами с положением покоя при нулевой длине. При этом положительные напряжения соответствуют констакнам (жёсткостям) пружин, а отрицательные напряжения таковы, что положение покоя этих элементов находится в бесконечности. Одним из достоинств нашего подхода является то, что силы являются линейной функцией положения, тогда как в инженерной установке вместо «истинной» энергии используется квадратичное приближение для получения сил как линейной функции перемещений из положения покоя. Более подробно это будет обсуждаться в дальнейшем.
Значение нуль-пространства («нулёвости») матрицы напряжений поясняется следующей леммой.
ЛЕММА 2. Пусть G(p) в R n имеет напряжение ω, а её аффинная оболочка p 1 ,…, pv в R n k-мерна. Тогда нулёвость Ω ≥ k+1. И наоборот, для данных Ω и n ≥ нулёвость Ω + 1 существует q = (q1,…,q v ) E R nv такой, что размерность аффинной оболочки q1,…,q v равна нулёвости Ω + 1. Более того, можно выбрать q так, чтобы pi было ортогональной проекцией qi на аффинную оболочку p1,…,p v .
Доказательство . Основная идея состоит в том, что если p1,….pv рассматривать как векторы-столбцы и объединить их в матрицу, то строки этой матрицы являются элементами нулевого пространства Ω, если предположить, что G(p) имеет напряжение ω.
Без ограничения общности можно положить pv = 0. Перенумеруем значения, если необходимо, чтобы p1,…,pk были линейно независимыми, где k — размерность аффинной оболочки p1,…,pk. По свойству D, указанному выше, можно считать pi = ei, i =1,…,k, где ei — i-й стандартный базисный вектор в Rn. Тогда векторы
(p1e1,…,pvei) E Rv, I = 1,…,k (***)
находятся в нуль-пространстве Ω, согласно свойству D (проекция на прямую через ei есть аффинное преобразование), и, очевидно, они линейно независимы в Rv. А поскольку последняя координата равна 0, то (1,…,1) вместе с указанными выше векторами также независим. Итак, мы нашли k+1 независимых векторов в нулевом пространстве Ω, то есть показали, что нулёвость Ω ≥ k+1.
И наоборот, предположим, что n ≥ нулёвость Ω +1 и pi E Rk. Обозначим l = нулёвость Ω. Нужно найти q-j=(q1j,…,qvj) E Rv, j = 1,…, l - k -1 такой, что вектор (1,1,...1) в (***) и q-1,…,q-l-k-1 охватывают нулевое пространство Ω. Тогда qi = (p1e1,…,piek,…,qi 1,qi 2,…,qil - k -1) E Rl+1, i=1,…,v указывают точки q = (q1,…,qv) E R(l+1)v такие, что G(q) имеет то же напряжение ω, что и G(p). Обратите внимание, что G(q) проектируется ортогонально на G(p) (мы по-прежнему считаем, что qv = 0). Лемма доказана.
Заметим, что эта лемма даёт нам геометрический метод поиска нуль-пространства Ω. А именно, если найти пространство наивысшей размерности, в котором G имеет реализацию с напряжением w, то нулёвость (размерность нуль-пространства) Ω будет на единицу больше, чем размерность этой реализации. Точнее говоря, Лемма 2 обеспечивает соответствие нулевых пространств матриц напряжений Ω реализациям графа G с максимальным размером оболочки аффинных линейных отображений.
Ниже получен очень простой результат, который мы позже используем.
ЛЕММА 3. Пусть A ( t ), 0≤ t ≤1 — симметричная матрица размером vxv , элементами которой являются непрерывные функции от t , а нулевое пространство A ( t ) постоянно для всех значений t . Тогда, если A (1) положительно полуопределена, то и A (0) также положительно полуопределена.
Доказательство. Ограничивая A(t) как дополнение к нулевому пространству, по условию, она положительно полуопределена в A(1) и, следовательно, для всех t. Таким образом, A(0) также положительна полуопределена.
Рассмотрим теперь выпуклые плоские многоугольники. Пусть (p1,...,pv)=p, где pi E R2, и пусть каждое pi лежит на границе выпуклого циклически упорядоченного многоугольника. Если каждое число pi можно отделить от других прямой линией, то говорят, что p - строго выпуклый (Рис. 9).
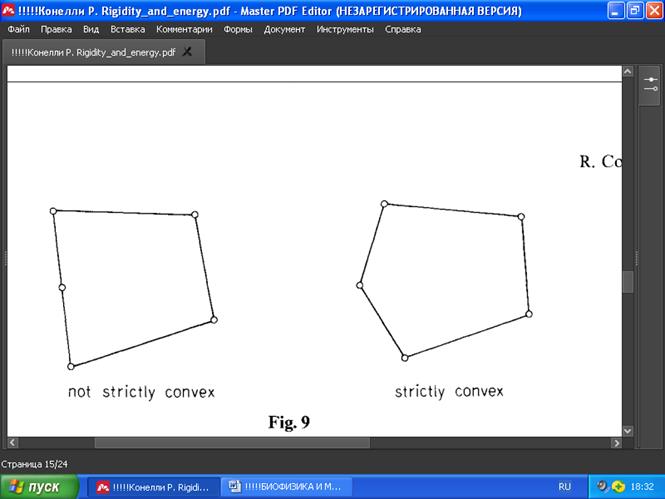
РИС. 9
Веедём понятие многоугольника Коши: по Коннелли [7], это плоская структура G(p), вершины p1,…,pv которой образуют строго выпуклый многоугольник, при этом рёбра (i, i+1), i = 1, 2,… , v — это тросы, а рёбра (i, i+2), i = 1,…, v-2 — это распорки (индексы по модулю v), как показано на Рис. 10.
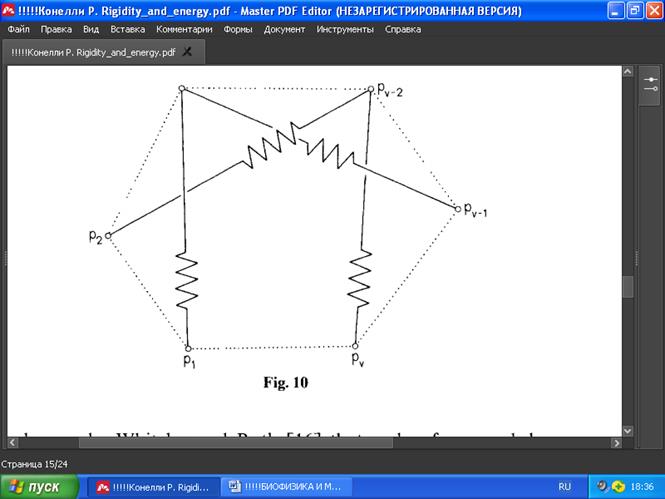
РИС. 10
Уайтли и Рот [16] показали, что такая структура имеет ненулевое собственное напряжение ω. Мы обобщим их доказательство, чтобы показать, что Ω является положительно-полуопределённой с нулёвостью 3.








