ЛЕММА 1. Пусть G — абстрактный каркас. Множество точек S: p E Rnv структуры G ( p ) имеет ненулевое собственное напряжение и замкнуто в Rnv.
Доказательство. Пусть p E Rnv — предельная точка множества S, определённого выше. Пусть p(i) E S — последовательность точек в Rnv, сходящаяся к p. Пусть w(i) E Re — ненулевое напряжение структуры G(p(i)). Заменяя w(i) на w(i)/│w(i)│, можно считать, что │w(i)│=1, то есть w(i) лежит на единичной сфере в пространстве Re. (Это можно сделать, поскольку уравнения равновесия для напряжений остаются в силе, если все напряжения умножаются на константу.) Поскольку единичная сфера компактна, то, взяв при необходимости подпоследовательность, мы можем считать, что w(i) сходится к ненулевому собственному значению w. (Обратите внимание, что неравенства, определяющие собственное напряжение, не являются строгими.) Функция, которая сопоставляет каждому p E Rnv, w E Re (равновесный) вектор (..., ∑ωjk(pj - pk),...), непрерывна, а поскольку она равна 0 для p(i), ω(i), то они сходятся к значениям p, ω таким, что градиент этой функции равен 0 для p, ω. Таким образом, G(p) находится в равновесии относительно ω, что означает, что ω является ненулевым собственным напряжением для G(p). Лемма доказана.
T ЕОРЕМА 3. Пусть G(p) — жёсткий каркас с тросами и распорками. Тогда G(p) имеет ненулевое собственное напряжение.
Доказательство ro . По Теореме 2, для любого ε>0 существует q такое, что |p−q| < ε и G(q) имеет напряжения на тросах и стойках, отличное от нуля. Согласно Лемме 1, тогда G(p) имеет ненулевое собственное напряжение.
Замечание 1. Хотя Теорема 2 гарантирует, что напряжение всех тросов и распорок близлежащего каркаса не равно нулю, для предельного процесса применительно к Лемме 1 это может быть не так. Например, некоторый трос может не иметь напряжения в равновесном состоянии структуры (Рис. 3).
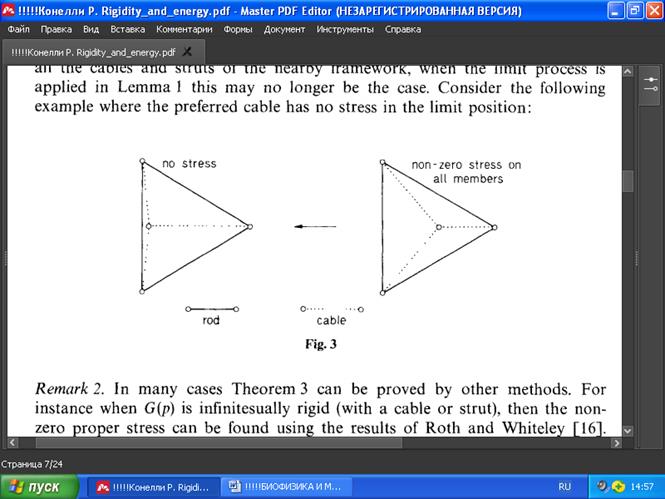
РИС .3
Замечание 2. Во многих случаях Теорему 3 можно доказать другими методами. Например, когда G(p) (с тросами и распорками) имеет бесконечно малую жёсткость, то ненулевое собственное напряжение можно найти, используя результаты Рота и Уайтли [16]. На самом деле, заключение Теоремы 2 верно, но при q = p - другими словами, G(p) «разрешает» напряжения в тросах и распорках без деформации. Однако я не вижу, как получить Теорему 3 с помощью этих методов в случае, если G(p) не имеет бесконечно малую жёсткость.








