II . Свойства жёстких структур
Исследуем сначала некоторые общие свойства жёстких структур, на основании чего окажется возможным дальнейшее рассмотрение и уточнение.
Предположим, что кто-то строит определённую структуру. На практике невозможно получить длины элементов абсолютно точно, и в любом случае всегда приходится с этим немного «играть». Однако, если каркас бесконечно жёсткий (см. Gluck [11] или Asimow и Roth [1]), то можно не сомневаться, что такие искажения будет несерьёзными для структуры в целом, то есть предельные искажения будут очень малы. Следующая теорема говорит, что это будет верно также, если каркас только предполагается жёстким, как определено во введении. Если G(p) - жёсткая, то одно из следствий состоит в том, что если G(q) является другой реализацией (формой) той же структуры, но при этом стержни имеют одинаковую длину, а тросы не длиннее и распорки не короче первоначальных, то множество таких q находится вне открытого множества Up E Rnv, содержащего все конгруэнтные реализации G(p). Другими словами, G(p) вкладывается однозначно, если ограничиться только теми преобразованиями, которые достаточно близки к реализациям, конгруэнтным G(p) (см. Коннелли [7]). Назовем Up жёсткой окрестностью точки p для G(p).
ТЕОРЕМА 1. Пусть G(p) — жёсткая в R n , и Up — жёсткая окрестность точки p для G(p). Пусть задано число ε > 0. Тогда существует число δ > 0 такое, что при q E Up выполнены следующие условия:
│ qi - qj │2 < │ pi - pj │2 + δ для тросов { i , j },
│ pi - pj │2 - δ < │ qi - qj │2 < │ pi - pj │2 + δ для стержней ( i , j }, (*)
│ pi - pj │2 - δ < │ qi - qj │2 для распорок (стоек) ( i , j ),
и существует жёсткая конгруэнция T в Rn такая, что
│( Tq 1 ,…, Tqv ) - p │ < ε.
Доказательство. Без ограничения общности, будем считать, что некоторая вершина G(p) (и G(q)) всё время остаётся неподвижной. Тогда множество q E Rnv, где G(q) конгруэнтно G(p), будет компактным. Пусть E E Re — множество, определяемое такими значениями (…, eij,…) E Re, что
eij ≤ │pi - pj│2 для тросов (i, j),
eij = │pi - pj│2 для стержней (i, j), и
eij ≥ │pi - pj│2 для распорок (i, j).
Пусть Vδ — открытая окрестность E в Re, определяемая значениями eij, заменяющими │qi - qj│2 в выражении (*) для любого δ>0. Пусть f: Up → Re — ограничение отображения жёсткости, определённого выше во введении, на окрестность жёсткости, определённую выше. Таким образом, Up является окрестностью обратной функции f -1 ( E ) в Rnv, если ограничиться только этими точками, скажем, неподвижной первой вершиной.
Предположим, что не существует числа δ>0 такого, как представлено выше. Тогда для каждого δ>0 существует точка q(δ) E Up - Uε такая, что f(q(δ)) E Vδ, где Uε — ε-окрестность обратной функции f -1(E) в Up. Можно считать, что cl U p - замыкание Up в Rnv - компактно, так как f -1(E) компактно, так как G(p) - жёсткая, а f -1(E) есть множество q E Rnv такое, что G(q) конгруэнтна G(p) с фиксированной (неподвижной) первой вершиной. В силу локальной компактности Rnv мы можем также считать, что G(p) однозначно вкладывается при ограничении на cl Up. Итак, существует последовательность положительных δi, i=1,2..., сходящаяся к 0, такая, что q(δi) E Up - Uε для всех i. При необходимости взяв подпоследовательность, можно считать, что q(δi) сходится к q E (Cl Up) - Uε. Но f(q(δi)) сходится к точке в E, поэтому f(q) E E и соответственно q E f-1(E). То есть мы получили противоречие. Таким образом, существует такое δ, что Uε E f-1(Vε). Другими словами, если q находится в пределах ε-окрестности от значения f-1(E), то некоторая конгруэнция G(q) находится в пределах ε-окрестности от G(p), как было сказано. Теорема доказана.
Предположим, у вас есть жёсткий каркас, и вы тянете или толкаете одновременно или последовательно две из его вершин. Тогда кажется «ясным», что если наша модель физически реальна, то каркас будет лишь слегка деформироваться и сопротивляться этой силе. Следующая теорема, предложенная У. Уайтли, говорит, почему именно так и бывает, только в нашем случае источником силы надо рассматривать тросы и распорки.
ТЕОРЕМА 2. Пусть G(p) — жёсткий каркас в Rn. Пусть задано ε>0. Тогда существует q E Rnv такое, что │p - q│< ε и G(q) имеет напряжение, не равное нулю на всех тросах и распорках.
Доказательство . Пусть δ>0 будет δ из Теоремы 1, тогда её заключение будет верным для указанных выше ε. Пусть ωij : I → R 1 — гладкие (не менее C2) функции энергии, определённые для каждого ребра, где I — соответствующий интервал, как показано на графиках ωij ниже (Рис.2). В каждом случае ωij → ∞ на асимптотах, при этом тросы и распорки монотонны с ненулевыми производными ωij, а для стержня есть только один минимум (производная равна 0).
Пусть N — окрестность точки p в Rnv, содержащаяся в жёсткой окрестности и такая, что (*) выполнено для q E N. Тогда справедлива Теорема 1. Для любого q E N определим энергию:
E(q) = 1/2 ∑ωij ( qi - qj )2 (**)
где сумма берётся по всем ребрам G. Как и в теореме 1, можно считать, что cl N компактно, если зафиксировать одну вершину графа G. Мы можем расширить определение E, включив сюда границу N и сделав E=∞ на границе. На расширенных действительных числах (включая ∞) E непрерывно, потому что, если │qi - qj│2 не находится в области определения напряжения ωij, то оно должно быть на одной из его асимптот, и все значения на близлежащих точках также будут большими. Таким образом, E должна иметь точку минимума q - E N. Заменяя q- жёсткой конгруэнцией в Rn по теореме 1, мы можем считать, что │q - p│< ε, а градиент E должен быть равен 0. Ппинимая n координат точки, как обычно, для градиента E получаем значения:
0 = (…, ∑ωij ’ ( qi - - qj - )2( qi - - qj - ),…),
где сумма берётся по рёбрам, смежным с i-й вершиной. Собственное напряжение определяется выражением ωij = ωij ’ │ qi - - qj - │2. В итоге мы получаем, что энергетическая функция является правильной (минимальной) и одновременно отличной от нуля для тросов и стоек. Теорема доказана.
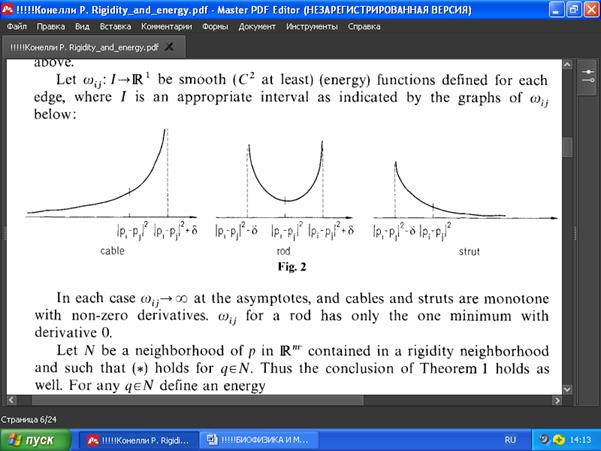
РИС . 2








