Жёсткость и энергия самонапряжённых структур
Р. Коннелли
Корнелльский университет, Математическое отделение, Итака, Нью-Йорк 14853, США
Inventiones mathematicae · февраль 1982
DOI: 10.1007/BF01404753
*Частично поддержано грантом NSF MCS -7902521.
Содержимое этой страницы было загружено Р. Коннелли 22 октября 2014 г.
Invent. math. 66, 11-33 (1982)
I . ВВЕДЕНИЕ
Предположим, человек держит в одной руке две палки в форме креста и натягивает на их четыре конца резиновую ленту. Когда полученная структура будет выпущена из рук, она примет форму выпуклого плоского четырёхугольника. Причём он всегда возвращается к той же форме, как бы она ни была искажена нами, пока не соскользнёт с концов или не порвётся резинка. Это очень простой пример «жёсткого»
каркаса из типа самонапряжённых структур («тенсегрити»), который мы здесь обсуждаем.
С энергетических позиций легко объяснить, почему являются жёсткими структуры, подобные приведённой выше: резинка деформируется таким образом, чтобы минимизировать общую энергию каркаса, то есть каркас будет иметь минимальную энергию только в конечной деформированной форме.
Идея введения энергетических функций очень полезна. Например, её можно использовать для доказательства ключевой леммы, которая использовалась Коши [5] в 1813 г. и показывает, что «выпуклые многогранные поверхности» являются жёсткими. Это может объяснить, почему некоторые, а возможно, и все произведения (структуры) тенсегрити Р.Бакминстера Фуллера [10] остаются в состоянии самонапряжения. В частности, применительно к паутине лемма показывает, почему она можетт принимать только определённые геометрические формы. Это также может использоваться для доказательства гипотезы 6 Бранко Грюнбаума и Г.К. Шепарда в их «Лекциях по утраченной математике» [12]: согласно этой гипотезе, если каркас в виде выпуклого многоугольника со стержнями (палками) на границе и тросами внутри является жёстким на плоскости, то жёсткий каркас получается и при перемене мест стержней и тросов.
Интересно сравнить некоторые из этих результатов с «раскрывающимся рукавом» в теореме Акселя Шура [18] (см. также Черна [6]), которая является очень близкой к гладкому аналогу леммы Коши. Теорема Шура утверждает, что если выпуклую плоскую гладкую дугу (плечо) разомкнуть, т. е. передвинуть на другое место той же длины, но с соответствующими точками меньшей кривизны, то два её конца раздвинутся (Рис.1).
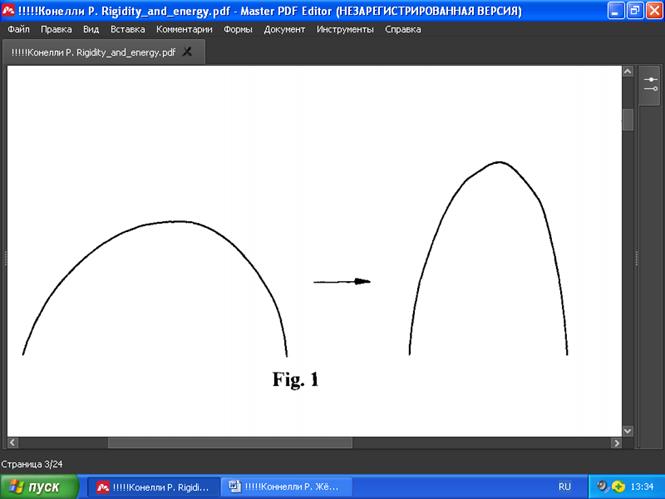
РИС . 1
Ещё одно конкретное приложение этого состоит в том, что можно показать, что у правильного пятиугольника в трёхмерном пространстве (пятиугольника, у которого равны все 5 сторон и все 5 углов между сторонами) все углы находятся в диапазоне между 360 и 1080 (примечание О. Боттема в [4]).
Мы в большом долгу перед Уолтером Уайтли за ряд предположений и очень показательные вопросы [23]. В частности, формулировки Теоремы 2 и теоремы 3 здесь, а также большая часть общего плана доказательства гипотезы 6 Б. Грюнбаума (здесь это Следствие 2) были частью его гипотез.
Здесь используются обозначения из работ Asimow and Roth [1] и Gluck [11], которые представляют собой абстрактный конечный граф, где каждое ребро обозначает стержень, трос или распорку. Реализация графа G, также называемая каркасом, будет обозначать расположение pi i-й вершины (узлов) графа G в пространстве Rn. Обозначим эти точки как один вектор p = (pi,..., pv) в пространстве (Rn)v = Rnv, где v — количество вершин графа G, а Rn — евклидово пространство с размерностью n. Обозначим реализацию графа, рассматриваемую в виде набора точек и рёбер в Rn, как G(p). Тогда непрерывное движение, или изгиб G(p) есть непрерывный путь p(t) в пространстве Rnv из точки p(0), где нормированное 0≤t≤1. При этом предполагается, что стержни имеют фиксированную длину, тросы не увеличиваются в длине, а стойки не уменьшаются в длине. Края G (стержни, тросы, распорки) часто называют элементами (обратите внимание, что члены G(p(t)) в общем случае могут пересекаться и проходить друг через друга даже при t=0).
Если p(t) имеет жёсткое ограничение при деформации, то говорят, что гибкость G(p) тривиальна. Если для G(p(t)) возможны только тривиальные изгибы, то говорят, что структура G(p) жёсткая.
Предположим, что q в Rnv — другое положение вершин графа G. Если стержни, тросы и распорки G(q) имеют длину не больше и не меньше таковой для соответствующих стержней, тросов и распорок G(p), то говорят, что G(q) есть другое вложение G(p) (обратите внимание, что при этом не обязательно симметричное отношение). Конгруэнция G(p) — это ограничение жёсткого глобального движения вершин G(p) в Rn (включая отражения). Если любое другое вложение G(q) группы G(p) конгруэнтно G(p), то говорят, что G(p) имеет однозначное вложение. Заметим, что если G(p) вложена однозначно, то G(p) заведомо жёсткая.
Зададим отображение жёсткости f: Rnv→R e, как у Глюка [11], у Азимова и Рота [1], но для более общего случая тросовых натяжных структур, формулой:
f( p 1 ,..., pv ) = (…,│pi - pj│2,…)
где (i, j) обозначает ребро G, а e — общее количество ребер (всех типов) G.
Напряжение ребра в G(p) — это скаляр ωij = ωji такой, что для всех i выполняется соотношение:
∑ ωij(pi -pj) = 0,
где сумма берётся по всем вершинам j, смежным с i (тогда также говорят, что структура G(p) находится в равновесии в вершине-точке pi относительно напряжений ω).
Часто все напряжения рёбер ωij рассматриваются как один вектор ω = (…,ωij,…) в пространстве размерностью Rv. При этом собственное напряжение G(p) — это напряжение ω такое, что ωij ≥ 0, если (i,j) — кабель, и ωij ≤ 0, если (i,j) — распорка (без условия для стержней). Это определение немного отличается от данного Ротом и Уайтли [16], которые определяют собственное напряжение как представленное
выше, но с дополнительным условием, что оно не равно нулю на всех тросах и распорках Мы для общности будем полагать, что некоторые из этих напряжений могут быть равны нулю.
В разделе II предполагается, что исследуются свойства некоторого заданного каркаса G(p), который является жёстким. Основная цель здесь состоит в том, чтобы показать, что жёсткая структура G(p) согласно Теореме 3 может иметь ненулевое напряжение на тросах и стойках, если они есть в структуре. Идея заключается в том, чтобы сначала показать, что общее требование жёсткости подразумевает, что согласно Теореме 1 элементы можно слегка ослабить, а структура (узлы) не будет перемещаться далеко от своего исходного положения,. Это позволяет определить функцию энергии с минимальным значением вблизи исходного положения, и поскольку градиент энергии должен быть равен нулю в этом минимуме, то тем самым гарантируется надлежащее предварительное напряжение, отличное от нуля на каждом тросе и стойке, согласно Теореме 2. Ограничивающий это аргумент приводит к Теореме 3.
Раздел III посвящён специальным структурам и квадратичным функциям энергии. После знакомства с работой квадратичных функций энергии на примере
каркасов в виде паутины (сети) рассматриваются выпуклые многоугольники. При этом, в частности, показывается, как определить «естественную» квадратичную форму энергии в терминах данного напряжения, и исследуется, когда эта форма является положительно полуопределённой для физической реализуемости. При этом оказывается, что когда выпуклый многоугольник имеет тросы на границе и распорки внутри и имеет собственное напряжение, то оказывается, что такая структура имеет положительно полуопределённую cэнергетическую форму с правой нулевой точкой, поэтому такой каркас однозначно вложен, Теорема 3 и гипотеза 6 Грюнбаума является прямым следствием этого.
В разделе IV обсуждается связь полученных здесь результатов с леммой Коши, теоремой Шура и теоремой Ван дер Ваардена.
В продолжении этой статьи мы надеемся объяснить отношение этих идей к инженерии и более общим энергетическим функциям.








