The Polygon Theorem. Any convex planar polygon with an equilibrium stress (and
corresponding stress matrix Ω), that is positive on the external edges and negative (or zero) otherwise, is super stable with respect to Ω.
(For a proof see R. Connelly [2])
Теорема многоугольника. Любой выпуклый плоский многоугольник с равновесным напряжением и
соответствующей матрицей напряжений Ω, положительной на внешних ребрах и отрицательной или равной нулю в противном случае, является сверхустойчивым по отношению к Ω.
(доказательство Р. Коннелли см. [2]).
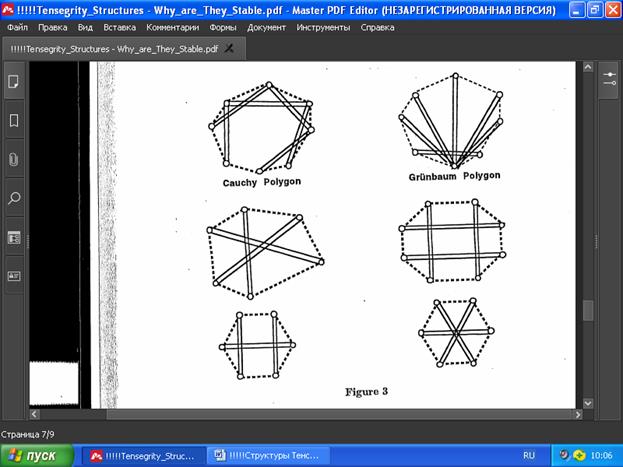
РИС. 3
Figure 3 shows some examples where the Polygon Theorem applies to guarantee super stability. The first two, the Cauchy polygon and Griinbaum polygon are part of a general class of polygons, and they happen to be infinitesimally rigid as well. As long as the vertices of the configuration p are part of a convex polygon, then the combinatorial structure, given by the graph G, will always give a super stable tensegrity G(p). On the other hand, the other polygons in the Figure depend on there being a particular conditions on the configuration, just to insure that there is a non-zero equilibrium stress. For example, the polygon on the middle left must have the vertices lie on an a conic (in addition to being convex). The other three polygons are drawn as regular polygons.
На рис. 3 показаны некоторые примеры применения теоремы многоугольника для гарантии сверхустойчивости. Первые два - многоугольник Коши и многоугольник Грюнбаума - являются частью общего класса многоугольников, они являются также бесконечно жёсткими. Пока вершины p структуры являются частью выпуклого многоугольника, комбинаторная структура, заданная графом G, всегда будет давать сверхустойчивую тенсегрити G(p). С другой стороны, другие многоугольники на рисунке зависят от определённых условий только для того, чтобы обеспечить ненулевое равновесное напряжение. Например, многоугольник в середине слева должен иметь вершины, лежащие на конике (помимо того, что он выпуклый). Остальные три многоугольника рисуются как правильные многоугольники.
Хорошим источником таких примеров является каталог высокосимметричных сверхустойчивых структур тенсегрити, разработанный совместно с Алленом Бэком (см. Коннелли, Бэк [3]). Смотрите также наш сайт по адресу:
http://math.lab.cit.cornell.edu/visualization/tenseg/tenseg.html
8. Объединение структур при суперпозиции.
Возьмём две разные структуры тенсегрити, каждую со своим равновесным напряжением, и наложим друг на друга некоторые из их вершин. Тогда комбинированное напряжение будет суммой матриц напряжений, рассматриваемых как квадратичные формы. Может даже оказаться, что некоторые напряжения могут аннулироваться, устраняя соответствующий трос или распорку. На рис. 4 показан пример этого:

РИС. 4
Обратите внимание, что при использовании этого метода с добавлением матриц напряжений каждый подграф, где каждое напряжение не равно нулю, должен перекрываться с другими таким образом, чтобы вся конфигурация находилась в евклидовом пространстве соответствующей размерности. В примере на рис. 2а каждый из меньших квадратов вынужден лежать в двумерном пространстве, но два следующих друг за другом квадрата имеют только две общие вершины - таким образом, существует «шарнир», благодаря которому вся конфигурация может вращаться в более высокие измерения.
На рис. 5 показано несколько примеров, в которых повторяется один и тот же блок для получения удлинённых форм. При этом верхний и нижний каркасы сверхустойчивы с суммой напряжений на соответствующих узлах в качестве стабилизирующих. В центральном примере, если принять в качестве стабилизирующего напряжения сумму напряжений на каждом шестиугольнике, ранг матрицы напряжений будет на единицу меньше требуемого в условии (4) раздела 5. Тем не менее, во всех случаях на рис. 5 конфигурация будет оставаться жёсткой в плоскости, даже если рассматривать её как трёхмерную.
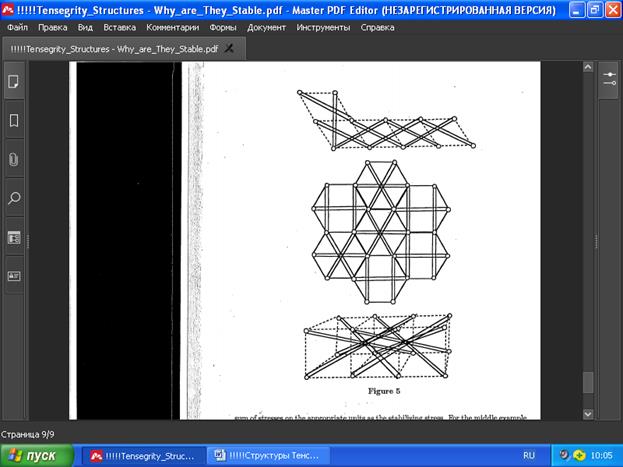
РИС . 5
Источники
1. R. Connelly and W. Whiteley, Second-Order Rigidity and Prestress Stability for Tensegrity Frameworks 9 (1996), no. 3, 453-491.
2. R. Connelly, Rigidity and Energy, Invent, Math. 66 (1982), 11-33.
3. R. Connelly and A. Back, Mathematics and Tensegrity, American Scientist, March-April (1998), 142-161.
4. D. Ingber, The Architecture of Life, Scientific American, January (1998), 48-57.
5. B. Roth and W. Whiteley, Tensegrity Frameworks, Trans. Amer. Math. Soc., 265 (1981), 419-446.
См. обсуждения, статистику и профили авторов этой публикации по адресу:
https://www.researchgate.net/publication/225203213








