РИС. 1. X -структура К. Снельсона - одна из простейших структур тенсегрити.
- Жёсткость: любая конфигурация q, достаточно близкая к p и удовлетворяющая ограничениям, конгруэнтна p.
- Бесконечно малая жёсткость (=Статическая жёсткость): здесь используется линеаризованная форма ограничений, заданная матричным неравенством R(p)p ' ≤ 0. Если оно имеет только минимальные тривиальные решения, заданные производными одного параметра конгруэнтного семейства, структура графа G(p) имеет бесконечно малую жёсткость.
-Общая жёсткость: это просто свойство базового графа G - если существует некоторая конфигурация p (с алгебраически независимыми координатами) такая, что G(p) - бесконечно жёсткая, то G называется жёсткой в общем.
- Жёсткость второго порядка: здесь используется движение первого порядка p' и требуется расширение p", удовлетворяющее соответствующим уравнениям.
- Устойчивость к предварительному напряжению: по отношению к G(p) это означает, что для каждой стойки и троса существуют потенциальные функции такие, что сумма по всем соседним конфигурациям q имеет квадратичный локальный минимум только тогда, когда q конгруэнтна p (более подробно это будет рассмотрено в следующем разделе).
~ Глобальная жёсткость: G(p) является линейно-жёсткой, если любая конфигурация q в Rd, удовлетворяющая ограничениям, конгруэнтна p.
- Сверхустойчивость: G(p) является сверхустойчивой, если существует конкретная положительная полуопределённая квадратичная форма, определённая для всех конфигураций q во всех измерениях, которая минимизируется, когда q является аффинным образом p (вместе с другими условиями, упомянутыми ниже).
3. Устойчивость к предварительному напряжению.
Я утверждаю, что наиболее важными понятиями устойчивости являются устойчивость к предварительному напряжению и сверхустойчивость, рассмотренные ниже.
Начнём с «идеальной» конфигурации p = (p1, p2,..., pn) и определим вещественнозначные потенциальные функции, областью определения которых являются положительные вещественные числа:
fi,j: R1+ → R1
для каждого ребра (i,j}графа G.
48
Полный потенциал любой конфигурации q определяется выражением:
E(q) = ∑fi,j│qi — qj│2.
Если E имеет невырожденный локальный минимум при q = p, единственный с точностью до жёсткой конгруэнтности, то говорят, что G(p) устойчива к предварительному напряжению. Коэфициенты fi,j определяют напряжённо-деформированные характеристики троса или стойки {i,j}, и будем предполагать, что все они дифференцируемы и имеют строго положительную вторую производную в области их определения, то есть положительно определены. Их потенциальная функция определяет (равновесное) напряжение:
Wi,j = 1/2 fi,j‘│pi — pj│2.
Знаки коэффициентов fi,j‘ будем интерпретировать как натяжение тросов - при положительном значении, и сжатие для распорок - при отрицательном значении.
Лемма. Если p является точкой экстремума потенциальной функции E, то указанные выше напряжения обеспечивают векторное равновесие в каждой вершине, то есть в каждой вершине выполняется векторное уравнение:
∑ wi , j ( pi — pj ) = 0 для каждого узла i.
На рис. 2 показаны некоторые примеры структур тенсегрити, устойчивых к предварительному напряжению (более полное их описание см. в [1]).
4. Гессиан.
Предположим, что w = (...,wi,j,...) являются равновесными напряжениями, как было указано выше. И определим (симметричную) матрицу напряжений Ω, где значение элемента {i,j} при i # j равно −wi,j и суммы строк и столбцов равны 0. Определим матрицу жёсткости R(p) с размерностью e x dn, каждая вектор-строка которой соответствует ребру (i,j) и имеет все элементы равными 0, за исключением двух элементов, равных pi — pj для вершины i и pj — pi для вершины j. При этом количество стоек и тросов структуры G равно e, количество вершин - n, окружающее пространство - Rd. Для каждого троса или стойки {i,j) определим коэффициент жёсткости в виде:
Ci,j = 1/4 fi,j‘‘│pi — pj│2,
и пусть D будет диагональной матрицей размерностью e x e с элементами ci,j > 0. Тогда символьные вычисления показывают, что гессиан потенциальной функции представляет собой симметричную матрицу:
H(E)= Ω®Id + R(p)tDR(p),
где Id — единичная матрица dxd, ()t — операция транспонирования, символ ® - тензорное произведение двух матриц. Второй член называется матрицей жёсткости и всегда является положительно полуопределённым. Вычисления повторяются для каждого набора координат.
На рис. 2 показаны некоторые примеры предварительно напряжённых структур. Обратите внимание, что структура на рис.2а не является жёсткой в трёхмерном пространстве, хотя её матрица напряжений является положительно полуопределённой, поскольку существуют аффинные преобразования структуры в виде изгибов (поворотов) в пространствах большей размерности. Структуры на рис.2a-e имеют бесконечно малую жёсткость в плоскости, поэтому они автоматически устойчивы к предварительному напряжению, поскольку квадратичная форма их матрицы жёсткости является определяющей при достаточно малых напряжениях. Октетная ферма Снельсона (рис. 2f) имеет положительно полуопределённую матрицу напряжений, но не обладает бесконечно малой жёсткостью в трёхмерном пространстве.
49
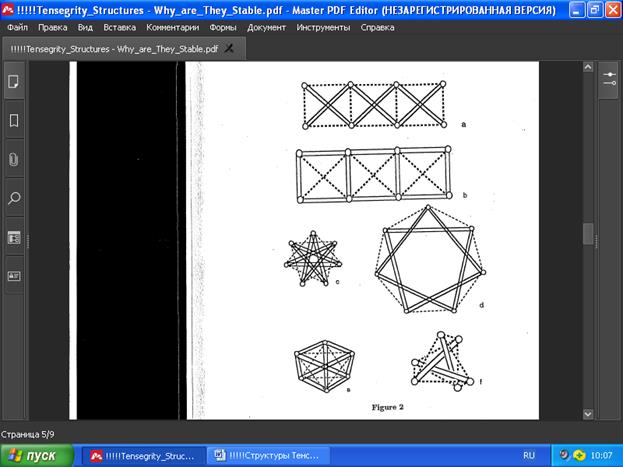
РИС. 2
5. Сверхустойчивость.
Устойчивость к предварительному напряжению имеет некоторые недостатки, особенно когда матрица напряжений Ω имеет отрицательные собственные значения. Здесь предлагается рассмотреть особый вид устойчивости к предварительному напряжению.
Структура тенсегрити G(p) с n вершинами в пространстве Rd является сверхустойчивой, если существует равновесные напряжения w = (..., wi,j,...) с матрицей напряжений Ω такой, что:
50
1) Напряжения wi,j положительны для тросов и отрицательны для распорок.
2) При i ≠ j значение элемента (i,j) матрицы Ω равно —wi,j и (1,1,...,1) Ω = 0 (это условие определяет симметричность матрицы Ω напряжений w).
3) Как квадратичная форма Ω положительно полуопределена.
4) Ранг Ω равен n—d—1 (наибольший из возможных).
5) В структуре G(p) нет аффинных (бесконечно малых) изгибов (поворотов).
Например, для X-структуры тенсегрити К. Снельсона матрица напряжений равна
1 -1 1 -1
Ω = -1 1 -1 1
1 -1 1 -1
-1 1 -1 1
и является положительно полуопределённой ранга 1 (обратите внимание, что если тросы и стойки поменять местами, то матрица напряжений НЕ будет положительно определённой!).
6. Свойства и преимущества сверхустойчивых структур.
Для сверхустойчивой структуры G(p) по отношению к равновесным напряжениям w в пространстве Rd выполняются следующие свойства:
1) Структура G(p), глобально жёсткая в любом пространстве Rk при k ≥ d, то есть любая другая конфигурация q в Rk, удовлетворяющая ограничениям по расстояниям, конгруэнтна (совпадает с) p.
2) G(p) устойчива к предварительному напряжению и дополнительно стабилизируется любыми положительными напряжениями w.
3) Если q — любой неособый афинный образ p, то G(q) сверхустойчива по отношению к тем же равновесным напряжениям w.
4) Если q — любое неособое проективное преобразование p, то существует подходящим образом изменённое равновесное напряжение w' (возможно, с изменением знака) такое, что соответствующая ему структура G'(q) сверхустойчива по отношению к w', где в G' соответствующим образом изменены значения напряжений распорок и тросов.
5) Должен быть подключен подграф G, определяемый только тросами.
6) Граф G, определяемый распорками и тросами, связан с (d+1) вершинами (узлами).
Свойство (2) является ключевым во многих физических ситуациях. Предположим, что структура тенсегрити имеет некоторое заданное равновесное напряжение w, определяемое физикой задействованных элементов. Если тенсегрити остаётся в определенной конфигурации в течение длительного периода времени, то разумно ожидать, что равновесные напряжения w задают состояние устойчивости с предварительным напряжением. Но что произойдет, если w увеличить без соответствующего увеличения коэффициентов жёсткости ci,j ? Матрица напряжений Ω здесь является определяющей, и если она имеет любое отрицательное собственное значение, то структура не будет оставаться в покое, даже если это равновесная конфигурация, посккольку малейшее возмущение приведёт к резкому изменению формы структуры. Однако, наоборот, положительные собственные значения влияют таким образом, что многие физические, химические и биологические структуры тенсегрити становятся сверхустойчивыми – тогда, каким бы сильным ни было равновесное напряжение по отношению к коэффициентам жёсткости, структура останется устойчивой до тех пор, пока не разрушатся её элементы. Когда конструкция сверхустойчива, увеличение предварительного напряжения лишь «укрепляет» её. Если же в матрице напряжений имеется отрицательное собственное значение, то увеличение предварительного напряжения приведёт к катастрофической ситуации и разрушению равновесной структуры.
Например, на рис.2b массив квадратов со стойками снаружи может иметь только равновесное напряжение с отрицательным собственным значением, несмотря на то, что сама эта структура тенсегрити бесконечно жёсткая в плане. Тогда, если предварительное напряжение q увеличилось в достаточной степени без соответствующего увеличения коэффициентов жёсткости ci,j, то конструкция разрушится, даже если она всё время остаётся плоской. С другой стороны, структура тенсегрити на рис.2а может иметь предварительное напряжение только при положительных собственных значениях, однако ранг её матрицы напряжений невысокий, что не позволяет ей быть сверхустойчивой строго по определению, поскольку.это не соответствует условию (6) выше. Хотя она сохраняет многие черты сверхустойчивой структуры, поскольку каждый из её квадратов очень стабилен и сохраняет свою форму, даже если им разрешено двигаться в трехмерном пространстве.
51
Структуры на рис.2d и рис.2f вполне сверхустойчивы, но обратите внимание, что форма октета Снельсона на рис. 2f имеет только три распорки и девять тросов, то есть в некотором смысле она имеет подкосы. А чтобы структура была бесконечно жёсткой, необходимо, чтобы общее число элементов в графе G' было хотя бы на единицу больше, чем 3n—6 = 12 для трехмерного пространства (за вычетом 6 движений структуры как целого – см. обсуждение этого, например, Roth и Whiteley [5]). В нашем случае существует ровно 12 элементов, поэтому одно только это количество означает, что матрица жёсткости имеет слишком малый ранг, чтобы обеспечить устойчивость к предварительному напряжению сама по себе. Однако, оказывается, что матрица напряжений не имеет отрицательных собственных значений и поэтому берёт на себя устойчивость даже при больших напряжениях. Обратите внимание, что лежащий в основе этой структуры граф такой же, как и для правильного октаэдра, однако он является бесконечно жёстким при наличии равновесного напряжения, тогда как треугольная сфера (такая, как октаэдр) не обладает бесконечно малой жесткостью именно тогда, когда она имеет равновесное напряжение.
Примечание. Здесь у кого-то может возникнуть искушение думать, что многие тенсегритии имеют подкосы, что снижает устойчивость, однако это не так.
Свойство (5) обнаруживается во многих примерах, где матрица напряжений имеет отрицательное собственное значение. Например, структура тенсегрити на рис. 2с имеет только два треугольника из тросов, и возможно перемещение этих двух треугольников по отдельности, но по отдельности жёстко и достаточно далеко друг от друга. Тогда квадратичная форма матрицы напряжений для этой структуры должна быть отрицательной, а значит, должно быть отрицательное собственное значение. Когда любое равновесное напряжение (с правильно выбранными знаками для каждого элемента) увеличивается, такая конструкция становится неустойчивой, хотя тоже обладает бесконечно малой жёсткостью.
Свойство (1) можно использовать непосредственно для обнаружения отрицательных собственных значений. Например, «тенсегрити на рис. 2с имеет ту же структуру, что и тенсегрити на рис. 2d. Действительно, на обоих рисунках тросы имеют одинаковую длину, однако стойки на рис.2d длиннее, чем на рис.2c, поэтому матрица напряжений для рис.2c должна иметь отрицательное собственное значение, в то время как тенсегрити на рис.2d является сверхустойчивой.
52
Можно ожидать, что в природе существует множество случаев появления сверхустойчивых структур. Много примеров и веских аргументов в пользу важности тенсегрити в биологической среде приводится в статье Ингбера [4].
7. Простые примеры сверхустойчивости .
The next question is: How does one construct super stable tensegrities? One category of super stable tensegrities to start further constructions is the following.
Следующий вопрос, который надо задать: как построить сверхустойчивые тенсегрити? Рассмотрим важную теорему с точки зрения начальных сведений для получения сверхустойчивости.








