Симметричные тенсегрити
Некоторые из наиболее привлекательных тенсегрити, сделанных Снельсоном, а затем и другими, очень симметричны, демонстрируя подгруппу симметрий куба или правильного додекаэдра. Чтобы быть эффективным в анализе и, что ещё важнее, обеспечить основу для классификации таких структур, удобно использовать теорию представлений конечных групп.
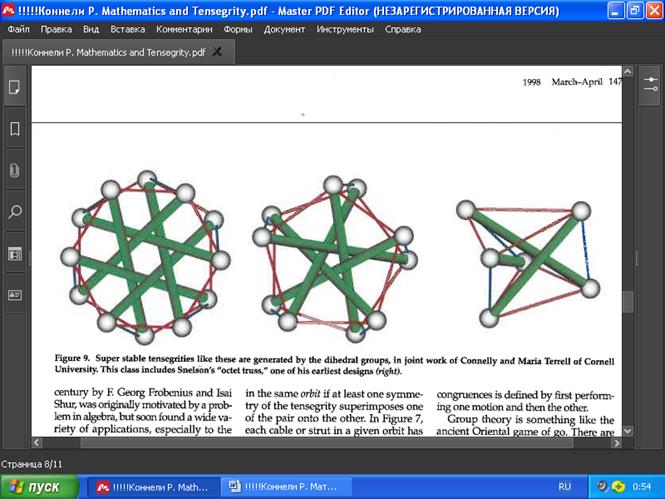
РИС. 9. Сверхустойчивые тенсегрити, подобные этим, генерируются двугранными группами в совместной работе Коннелли и Марии Террелл из Университета Коннелла. Этот класс включает в себя «октетную ферму» Снельсона, одну из самых ранних конструкций (справа).
Теория представлений конечных групп, разработанная на рубеже прошлого века Э. Георгом Фробениусом и Исай Шуром, первоначально была мотивирована проблемами в алгебре, но вскоре нашли широкое применение, особенно в физике новой тогда теории атома. Типичная история успеха начинается с довольно сложной математической модели конструкции с некоторой формой (геометрической) симметрии. Теория представлений позволяет разбить сложную модель на заранее определённое небольшое число гораздо более удобных моделей, каждую из которых можно рассматривать более или менее независимо. Фан Чанг и Шломо Стенберг (1993) привели очень хороший пример такого применения: анализ инфракрасных спектров бакибола - молекулы с 60 атомами углерода, имеющей симметрию правильного додекаэдра. В нашей ситуации теория представлений используется почти так же, за исключением того, что лежащие в её основе математические объекты различны.
Предположим, что тенсегрити можно вращать вокруг некоторой линии таким образом, что повёрнутая тенсегрити неотличима от оригинала: каждая вершина наложена на вершину, каждый трос наложен на трос, а каждая распорка наложена на другую распорку. Все движения, накладываемые таким образом (конгруэнтности тенсегрити), сами по себе образует математическую структуру, называемую группой симметрии (она может включать в себя и некоторые другие соответствия-преобразования и всегда опирается на «идентичность», то есть на дзен-подобное движение, которое просто оставляет всё нетронутым). Если тенсегрити имеет достаточно симметрий, что любая вершина может быть наложена на любую другую совмещением (конгруэнцией), то говорят, что группа симметрий транзитивна по вершинам. Точно так же любая пара вершин (как и любая пара кабелей или любая пара распорок) считается находящейся на одной и той же орбите, если по крайней мере одна симметрия тензогрити накладывает одну из пары на другую.
Например, на рис. 7 каждый кабель или стойка на одинаковой орбите имеют один и тот же цвет. Группа симметрий этих тенсегрити транзитивна на стойках (поскольку есть только одна орбита, окрашенная в зелёный цвет), но не совсем транзитивна на тросах (поскольку есть две орбиты, окрашенные в красный и синий цвета).
Учитывая всё это, легко проверить, существует ли равновесное напряжение для тросов и распорок: это выполняется, если существует какая-либо энергетическая функция, минимизируемая данной конфигурацией имеющая ту же симметрию, что и сама тенсегрити. Таким образом, каждому кабелю или стойке на любой заданной орбите может быть присвоено одинаковое напряжение. Точно так же баланс напряжений можно проверять только в одной вершине, поскольку все вершины одинаковы по группе симметрий. Почти для всех рассматриваемых здесь примеров оказывается легко проверить, что единственными аффинными движениями, которые сохраняют связи троса и распорки, являются конгруэнции. Следовательно, остается только одна трудность, прежде чем можно будет применить принцип наименьшей работы: мы должны убедиться, что энергия минимальна. Именно здесь на сцену выходят групповые отображения.
ОТОБРАЖЕНИЯ ГРУППЫ
До сих пор группы появлялись только в одном обличье - группа симметрий тенсегрити. Но группы также могут быть определены абстрактно, без привязки к какому-либо конкретному физическому объекту. С этой точки зрения группа — это просто множество, элементы которого могут «умножаться» и которое подчиняется определённым правилам, таким, как существование или значения идентичных элементов. В только что представленном случае элементы группы были движениями, которые накладываются на тенсегрити, а «умножение» двух конгруэнтностей определяется выполнением сначала одного движения, а затем другого (в общем случае, не наоборот). Поэтому теория групп чем-то напоминает древнюю восточную игру «го», в которой есть всего несколько простых правил и их легко усвоить, но чтобы справиться с их последствиями, могут потребоваться многие годы интенсивного изучения.
Подобно определённым последовательностям движений (или «дзёсэки») в «го», определённые группы движений встречаются достаточно часто, чтобы иметь собственные названия. Простейшей и, возможно, самой распространенной является группа из двух элементов, называемая Z2. Её элементы можно рассматривать как числа +1 и -1 с операцией умножения (обратите внимание, что при этом произведение +1 или -1 на +1 или -1 снова дает +1 или -1, что очень важно для группы идентичных элементов), также их можно рассматривать как слова «чётный» и «нечётный» с операцией сложения или представить как тождественное движение и отражение в зеркале.
Из множества обличий, которые может принимать абстрактная группа, одним из наиболее удобных являются наборы линейных функций. Вращения и отражения являются примерами линейных функций. Если элементы абстрактной группы мыслить как актёров, а линейные функции — как их роли, то афиша, которая назначает определённых актеров определённым ролям, называется представлением группы. Сама абстрактная группа могут использоваться для групповых вычислений и эффективно обеспечивать общую точку отсчёта. Представление, с другой стороны, может быть более структурированным и может давать глубокую и тонкую информацию об абстрактной группе.
Существенным понятием при работе с представлениями является понятие эквивалентности. Рассмотрим, например, группу симметрии слова МОМ. Есть два способа наложить это слово на себя: либо оставить его в покое (тождественное движение), либо отразить его относительно вертикальной линии, проходящей через центр O - таким образом, эта группа симметрии является представлением абстрактной группы Z2. Точно так же, если бы мы перевернули слово MOM набок, его группа симметрии по-прежнему была бы представлением Z2, хотя фактическое отражение здесь иное — теперь это отражение через горизонтальную линию, однако, существенная симметрия слова не изменилась при повороте его набок. Математик сказал бы, что эти два представления Z2 эквивалентны.
Сравним это с группой симметрий слова MOW. Опять же, есть два способа наложить это слово на себя: тождество и поворот на 180 градусов вокруг центра буквы O. Эта группа симметрии также является представлением Z2, но почему-то она ощущается по-другому. Разница здесь не в самой группе, а в геометрии: задействованная здесь линейная функция — это вращение, а не отражение. Таким образом, математик сказал бы, что это представление Z2 не эквивалентно предыдущему.
Симметрии трёхмерных фигур включают представления некоторых более интересных групп, чем Z2. Группа вращений куба и группа всех симметрий правильного тетраэдра являются представлениями группы перестановок четырех элементов, обозначаемой как S4. Эти два представления S4 оказываются не эквивалентными, как видно из рис. 8.
Представления групп могут быть объединены простым, но важным для применения способом. Например, подумайте о двух представлениях группы - одно как движение в трёхмерном пространстве, а другое как движение в двухмерном пространстве. Теперь представьте себе 5-мерное пространство, где первые три координаты соответствуют 3-мерному пространству, а следующие две координаты соответствуют 2-мерному пространству. Создайте новое представление группы, позволив первому представлению воздействовать на первые три координаты, а второму представлению - воздействовать на следующие две координаты. Тогда новое представление называется суммой двух представлений.
Иногда возможен и обратный процесс: при заданном представлении его можно разбить на сумму представлений меньшей размерности. Например, каждый из двух элементов в группе симметрии слова MOM накладывает на себя горизонтальную линию, проходящую через центр буквы O, и точно так же каждый элемент накладывает на себя вертикальную линию - таким образом, это представление сводится к сумме двух одномерных представлений. Однако, для двух трёхмерных представлений группы S4 ситуация иная: хотя здесь линия или плоскость могут быть наложены сами на себя путём индивидуального вращения, нет линии или плоскости, наложенных на себя всеми симметриями куба или Тетраэдра - такие представления называются неприводимыми.
Одним из главных открытий Фробениуса и Шура было то, что любое представление может быть разложено по существу единственным образом на неприводимые. Следовательно, неприводимые представления являются строительными блоками теории, как и простые числа в теории чисел.
Теперь мы можем определить представление, очень тесно связанное с функцией энергии для тенсегрити. Любая группа, например группа S4, имеет представление в виде перестановки своих собственных элементов (если вернуться к актёрско-ролевой метафоре, это похоже на то, как каждый актер играет самого себя). Поскольку S4 имеет 24 элемента, представьте себе пространство с 24 координатами, где каждая ось координат помечена одним элементом группы. Каждый элемент S4 соответствует перестановке осей, и каждое из них естественным образом продолжается до конгруэнтности 24-мерного евклидова пространства. Эти сравнения образуют регулярное представление S 4.
Фробениус доказал, что регулярное представление любой группы «содержит» все неприводимые, каждое из которых повторяется число раз, равное его размерности. Например, для S4 неприводимыми представлениями являются два трёхмерных, проиллюстрированные выше, а также 2-мерное, нетривиальное 1-мерное представление и тривиальное 1-мерное представление (где все элементы группы представлены как различаемые). Таким образом, в обычном представлении два трёхмерных представления повторяются три раза, что составляет размер каждого; равный девяти; двумерное представление повторяется дважды с учётом четырёх измерений; а нетривиальные и тривиальные одномерные представления учитывают ещё одно измерение каждое. В итоге, всего мы получаем 9+9+4+1+1=24 учитываемых измерения.

РИС . 10. Как построить тенсегрити своими руками: сделайте прежде картонную модель соответствующего правильного многогранника (а), вырежьте его стороны и используйте дырокол для бумаги, чтобы сделать отверстия в нужных точках на каждой стороне ( b ). Лучше всего, если размер отверстий позволяет проходить палочкам (здесь отверстия показаны крупными для ясности). Местоположение не обязательно должно быть точно правильным. Снова соедините края скотчем и проткните многогранник дюбелями в соответствии с тем, как они выглядят в финальном тенсегрити (с), (Сравните с рис. 7). Вставьте резиновые ленты в соответствующем порядке через выемки на концах распорок ( d ). На рисунке показаны штифты на концах дюбельных стоек, что тоже работает. Отрежьте картон и дайте всей конструкции прийти в равновесие. Замените резинку шнуром (резиновые ленты могут испортиться в течение нескольких недель).
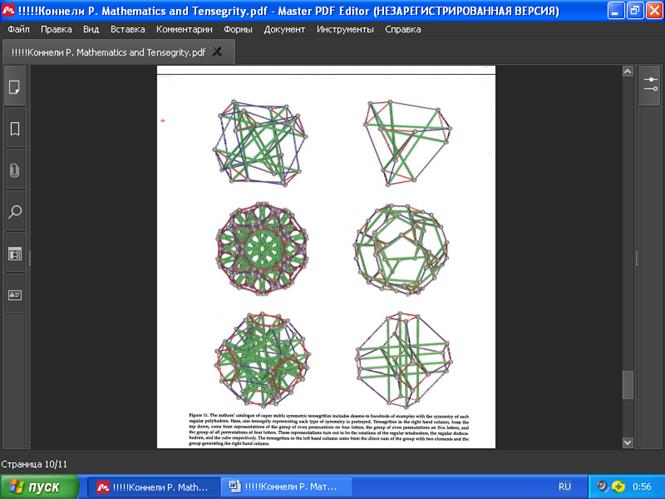
РИС. 11. Авторский каталог сверхустойчивых симметричных тенсегрити включает десятки и сотни примеров с симметрией каждого правильного многогранника. Здесь показана лишь одна тенсегрити, представляющая каждый тип симметрии. Тенсегрити в правой колонке, сверху-вниз образуются от представлений группы чётных перестановок четырёх элементов, группы чётных перестановок пяти элементов и группы чётных перестановок четырёх элементов - эти представления оказываются поворотами правильного тетраэдра, правильного додекаэдра и куба соответственно. Тенсегрити в левой колонке образованы от прямой суммы группы с двумя элементами и группы, порождающей правую колонку.
Предположим, что у нас есть тенсегрити, группа симметрий которой транзитивно действует на вершинах. Её энергетическая функция, определённая с помощью напряжений (мотивированных из условия равновесия), соответствует регулярному представлению группы симметрии. Сначала это было для нас вовсе не очевидно, и только проверив несколько частных случаев, мы обнаружили, что теорема Фробениуса не годится для нашего случая. С использованием этой теоремы функция энергии записывается в виде суммы функций энергии, соответствующих каждому из неприводимых представлений - таким образом, расчёты могут быть выполнены для гораздо меньших размерностей неприводимых конфигураций. Например, тогда вычисление минимальной энергетической конфигурации для группы S4 без декомпозиции, вытекающей из теории представлений, потребует решения уравнений как минимум с 24 переменными! При использовании же неприводимых представлений здесь требуется только два вычисления с тремя переменными, одно вычисление с двумя переменными и одно с одной переменной.
Теперь рассмотрим проблему немного по-другому. Начнём с напряжений, а затем спросим, есть ли у одного из представлений равновесная конфигурация для этого набора напряжений? Это похоже на поиск улыбки Чеширского кота (хозяйки) до того, как мы найдем саму кошку (тенсегрити). Если все напряжения положительны, то ясно, что все слагаемые в определении функции энергии положительны или равны нулю. Если канатный граф связен, это означает, что единственным представлением, дающим равновесную конфигурацию, будет тривиальное представление, в котором все вершины находятся друг над другом. Далее выберите одну из орбит, которые вы в конечном итоге хотите сделать опорой, и уменьшите коэффициент напряжения для этой стойки, даже позволяя ей быть отрицательной - продолжайте уменьшать этот коэффициент до тех пор, пока функция полной энергии не начнёт принимать значения на границе отрицательных значений (то есть нуля). Тогда хотя бы одно из нетривиальных неприводимых представлений имеет конфигурацию, равновесную относительно этого напряжения. Назовём эти равновесные конфигурации, возникающие в результате применения неприводимых представлений, критическими конфигурациями. Обычно, но не всегда, оказывается, что существует только одно представление, имеющее критическую конфигурацию - если это так, то эта желаемая конфигурация и есть соответствующая тенсегрити.
Одна тревожная черта этого процесса заключается в том, что, по-видимому, заранее нет никаких гарантий относительно того, какое представительство будет тем, которое обеспечит требуемые напряжения. Если один из «победителей» оказывается трёхмерным отображением (как это было во многих случаях, которые мы пробовали), то мы реально получаем сверхустойчивую тенсегрити, которую можно осязать и изучать, а не просто делаем вывод о её существовании в каком-то более высоком измерении. Но мы не знаем ни одной общей теории, которая предсказывала бы
результат без расчёта.
Однако, в трёхмерном пространстве не так много абстрактных групп, которые могут быть конечными группами симметрий. Они включают два бесконечных семейства: циклические группы на n элементах (которые можно отождествить с поворотами правильного n-стороннего многоугольника) и диэдральные группы с 2n элементами (группа всех симметрий, включая отражения, правильного n-угольника, двусторонний многоугольник). Есть и шесть других возможностей: S4; «переменные группы» A4 и A5 с 12 и 60 элементами соответственно; и «прямая сумма» каждой из них с группой Z2, которая удваивает количество элементов. Каждая из этих шести групп может быть представлена как группа или подгруппа симметрии правильного многогранника: например, группа вращений правильного додекаэдра является представлением A5.
Для любой заданной конечной группы наш метод позволяет эффективно составить полный каталог симметричных тенсегрити с двумя орбитами кабелей, одной
орбитой стоек и одной орбитой вершин. Самое интригующее и обнаруженное совсем недавно — это то, что элементы соответствуют шести группам, упомянутым в последнем абзаце. Поскольку распорки можно соединить с кабелями сотнями различных способов, сохраняя симметрию, то полный каталог содержит более сотни различных тенсегрити. Для рис. 11 мы выбрали по одному представителю для иллюстрации каждого из шести возможных типов симметрии. Полный каталог можно просмотреть на нашей странице в Интернете по адресу http://mathlab.cit.cornell.edu/visualization/tenseg/tenseg.html.
На рис. 10 показано, как сделать тенсегрити своими руками. Хотя
количество типов таких конфигураций конечно, остается ещё много места для художественных экспериментов: например, длины стоек можно выбирать более или менее произвольно (при условии, что все они имеют одинаковую длину), соответственно изменяются расположение и длина других членов. Делаем тенсегрити сначала с резиной (резиновые ленты помогают тенсегрити «найти» сверхстабильную конфигурацию), а дизайн затем можно сделать постоянным, заменив резиновые ленты на верёвку.
Для читателей, желающих построить виртуальные тенсегрити, мы рекомендуем программу STRUCK Джеральда де Йонга и Карла Эриксона. Эта программа доступна во всемирной паутине по адресу: http://wolfenet.com/-setebos/springspace.html
БЛАГОДАРНОСТИ
Авторы благодарят Дану Маккензи за прекрасное редактирование при подготовке этой статьи. Коннелли также благодарит Фонд Александра фон Гумбольдта за их щедрую поддержку в 1991-92 учебном году, когда были развиты многие идеи этой статьи.
ИСТОЧНИКИ
Chung, F., and S. Sternberg: 1993, Mathematics and the buckyball. American Scientist 81:56-71.
Connelly, R. 1980: Rigidity and energy. Inventiones Mathematicae 66:11-33.
Connelly, R., and M. Terrell: 1995. Globally rigid symmetric tensegities. Structural Topology 21:59-78.
Connelly, R. , and W. Whiteley: 1996. Second order rigidity and prestress stability for tensegrity frameworks. SIAM Journal of Discrete Mathematics (9)3:453-491.
Hartog, J. P. 1949: Strength of Materials. New York: Dover, pp. 3-4.
Lyuaternik, L. A. 1956: Convex Figures and Polyhedra. New York: Dover.
New York Academy of Sciences. 1989. Kenneth Snelson: The Nature of Structure. New York: New York Acadensy of Sciences.
Pugh, A. 1976. An Introduction to Tensegrity. Berkeley and Los Angeles, Calif.: University of California Press.
Snelson, Kenneth, Kenneth Snelson. <http://www.teleport.com/~pdx4d/snelson.html>.
Март-апрель 1995 года
Роберт Коннелли — профессор и заведующий кафедрой математики Корнельского университета. Он получил докторскую степень по математике Мичиганского университета в Анн-Арборе. Представитель Института высших научных исследований в Бюрес-сюр-Иветт, Университета Диона и Университета Шамбери во Франции, Университета в Сиракузах, Университета Монреаля, Университета Этвош в Будапеште и Университета Билефельда в Германии. Его исследования посвящены дискретной геометрии, в частности, изучению жёстких и гибких каркасов, дистанционной геометрии, упаковок и покрытий, а также форм астероидов.
Аллен Бэк - Директор Лаборатории учебных вычислений математического факультета в Корнелле. Он получил степень доктора философии, по математике Калифорнийского университета в Беркли. Его интересы включают дифференциальную геометрию, топологию, твёрдотельное моделирование, робототехнику, динамические системы и производство математического программного обеспечения.
Адрес Р. Коннелли: Корнелльский университет, Математический факультет, Уайт-холл, Итака, Нью-Йорк 14853.
Интернет: connelly@math.cornell.edu
Rigidity Theory and Applications:
Edited by Thorpe and Duxbury, Kluwer Academic/Plenum Publishers, 1999








