Устойчивость плоских тенсегрити
Квадратичные функции энергии для тенсегрити паутины работают очень хорошо, но если есть распорки (или внешнее крепление тросов), то ситуация усложняется: хотя энергетическая функция также определяется напрямую, появляются отрицательные константы пропорциональности для элементов. Полная энергия есть, как и прежде, сумма энергий каждого из тросов и распорок, в итоге в исходном положении стойка может иметь бесконечную длину! И хотя только что описанная функция энергии не является физически реализуемой, она не полностью оторвана от инженерной практики: если анализировать локальные статические свойства конструкции, то описывающая её квадратичная функция энергии является суммой двух слагаемых (положительного и отрицательного), рассматриваемых при достаточно малых возмущениях конструкции. И когда с помощью такого квадратичного приближения обнаруживается устойчивость, конструкция называется в инженерной литературе устойчивой к предварительному напряжению (преднапряжённой).
Если рассматривать только малые возмущения физической энергии предварительно напряжённой устойчивой конструкции, то второй член (который мы пока не описали) только увеличивает устойчивость конструкции (поскольку вычитается из положительной части для тросов). Действительно, для сверхустойчивой тенсегрити, пока нет катастрофического коробления распорок или разрыва тросов, увеличение напряжения имеет тенденцию лишь стабилизировать тенсегрити (то есть тенсегрити необязательно стабильна только до напряжения, как это бывает в известных физических системах!).
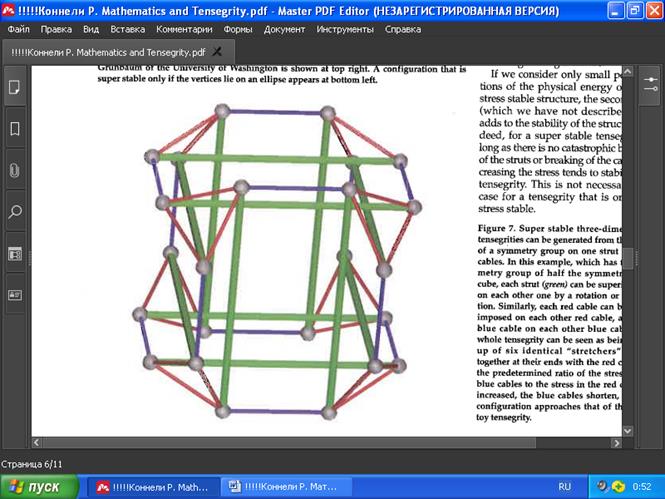
РИС. 7. Сверх устойчивые тр ё хмерные тенсегрити могут быть получены в результате действия группы симметрии на одну стойку и два троса. В этом примере, который составляет группу симметрий из половины симметрий куба, каждая стойка (зел ё ная) может быть наложена друг на друга пут ё м поворота или отражения. Точно так же каждый красный кабель может быть наложен на другой красный кабель, а каждый синий кабель — на каждый другой синий кабель. В с ю тенсегрити можно рассматривать как составленн ую из шести одинаковых «носилок», соединенных на концах красными тросами. Если увеличить заданное отношение напряжения в синих тросах к силе в красных тросах, то синие тросы укорачиваются, и конфигурация приближается к тенсегрити в виде известной детской игрушки.
Вторая проблема, когда мы переходим от паутины к тенсегрити — это отсутствие закреплённых вершин, что технически исключает предыдущую идею единственности минимума энергии: поскольку теперь ничего не закреплено, всю конфигурацию можно жёстко перемещать, при этом внутренняя энергия останется прежней. Даже не только это, но также массивные искажения конфигурации (определённые виды масштабных преобразований, а также проекции тенсегрити – её «тени» с меньшим числом измерений) могут теперь не изменять энергию. Условие равновесия сохраняется при таких отображениях, которые называются линейными аффинными преобразованиями (см. рис. 5).
Как и раньше, назовём коэффициент функции энергии для каждого троса или распорки напряжением. Как и в случае с паутиной темсегрити, говорят, что тенсегрити с этим набором напряжений находится в равновесии, если напряжения уравновешиваются в каждой вершине. Например, X-структура Снельсона находится в равновесии, когда все её четыре троса имеют напряжение +1, а две стойки имеют напряжение -1. Как и в случае с паутиной, если тенсегрити имеет энергетическую функцию, которая минимизируется для определённой конфигурации, то конфигурация находится в равновесии. Однако, обратное уже неверно (!): даже когда конфигурация находится в равновесии для данного набора напряжений, энергия может не быть минимальной. Например, просто поменяйте местами тросы и распорки для Х-тенсегрити Снельсона, а также поменяйте местами знаки напряжений - эта тенсегрити будет по-прежнему находиться в равновесии, но энергия будет уже на максимуме, а не на минимуме, и тенсегрити не будет сверхустойчивой (мало того, она не будет даже просто устойчивой).
Чтобы доказать, что данная тенсегрити является сверхустойчивой, мы должны рассмотреть три задачи. Во-первых, мы должны показать, что функция энергии находится в минимуме, а не только в равновесии. Во-вторых, мы должны показать, что единственными аффинными преобразованиями, которые не нарушают никаких ограничений тросов и распорок, на самом деле являются конгруэнтности (то есть не допускается ни растяжение, ни сжатие). Наконец, мы должны показать, что данная тенсегрити не может быть проекцией («тенью») любой тенсегрити высшего измерения, которая также находится в равновесии (последнее свойство Мария Террелл из Корнельского университета назвала универсальностью тенсегрити.) В этих условиях принцип наименьшей работы подразумевает, что данная тенсегрити сверхустойчива.
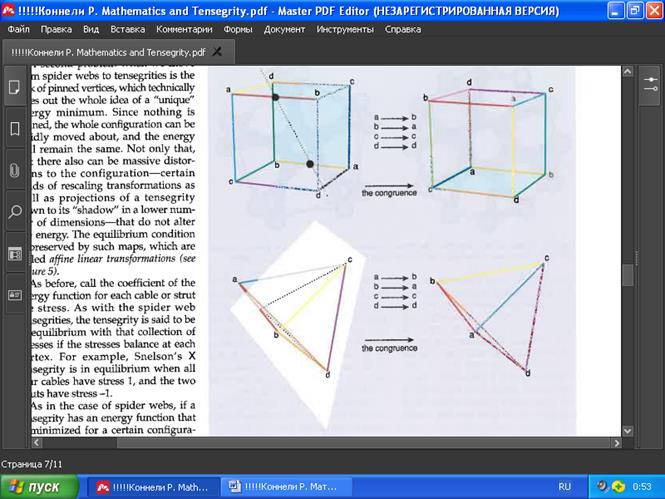
РИС . 8. Группа перестановок четырёх элементов действует на куб и тетраэдр двумя разными способами. На кубе (вверху) перестановка, которая переключает вершины с метками ( s ) на вершины с метками ( b ), оставляя неизменными только (с) и ( d ), представляет собой поворот. На тетраэдре (внизу) та же самая перестановка представляет собой отражение. Таким образом, видно, что группа перестановок четырёх элементов (называемая S 4 ) имеет два различных трёхмерных представления.
Такой подход позволил выявить большое количество сверхустойчивых тенсегрити. Например, возьмём любой выпуклый многоугольник на плоскости, рёбра которого — тросы, а некоторый набор внутренних диагоналей — распорки. (Здесь слово «выпуклый» применяется в другом контексте, чем раньше - многоугольник является выпуклым, если отрезок, соединяющий любые две его вершины, полностью содержится внутри многоугольника). Один из нас (Коннелли) доказал в 1980 году, что если может быть найден равновесный набор напряжений, положительный на внешних (краевых) тросах и отрицательный на внутренних (диагональных стойках), то выполняется каждое из трёх перечисленных выше условий - таким образом, любая такая тенсегрити является сверхустойчивой. Следовательно, для этого класса выпуклых плоских тенсегрити, как и для паутины, равновесие подразумевает устойчивость (см. рис. 6).
Остаётся вопрос, как сделать правильное обобщение для трёхмерного пространства. Естественным выбором конфигурации является набор вершин 3-мерного многоугольника, и, возможно, его края должны включать кабели тенсегрити. Но неясно, как точно определить удовлетворительно общий класс сверхустойчивых напряжений. Одна идея состоит в том, чтобы несколько специализироваться и посмотреть на напряжения, которые имеют большую симметрию. Во всяком случае, это можно использовать для сокращения неприятной части вычислений.








