Математика структур тенсегрити
R. Connelly
Cornell University
Allen Back
Cornell University
American Scientist , Volume 86 , March 1998
DOI: 10.1511/1998.2.142
См. обсуждения, статистику и профили авторов этой публикации по адресу:
https://www.researchgate.net/publication/274341141
Роберт Коннелли и Аллен Бек:
«Теория представлений групп позволяет составить полный каталог самонапряжённых структур типа «связывающие тросы – отдельные распорки» с заданными симметриями и свойствами»
Март - Апрель 1998
ВВЕДЕНИЕ
Осенью 1948 года, экспериментируя со способами строительства гибких модульных башен, молодой художник Кеннет Снельсон создал нечто вроде скульптуры, которую раньше никто не видел: эфемерная и подвижнаяя с виду, без видимых несущих элементов, тем не менее, она сохраняла свою форму и устойчивость. «Я был весьма поражен тем, что сделал», — вспоминал Снельсон четыре десятилетия спустя. Следующим летом он показал скульптуру своему наставнику, ещё не известному изобретателю, художнику и самозванному математику Р. Бакминстеру Фуллеру. Вскоре Фуллер адаптировал изобретение Снельсона как центральный элемент своей системы синергетики, вплоть до того, что назвал «свои» новые структуры именем «тенсегрити», название которых и известно сегодня (объединение двух слов integrity – «целостность» и tension – «напряжение»), и продвигал их в своих многочисленных вдохновляющих свободных лекциях.
Скульптуры Снельсона, в которых жёсткие стойки, или «элементы сжатия» (как их мог бы назвать инженер) подвешены в воздухе на почти невидимых тросах или очень тонких проводах, что сегодня уже можно увидеть во всём мире. Замечательная скульптура «Игольчатая башня» высотой 60 футов выставлена в Музее и Саду скульптур Хиршхорна в Вашингтоне, округ Колумбия. Идея проникла и в низкое искусство. В ряде детских игрушек используются те же принципы, что и в оригинальных структурах Снельсона. Можно даже утверждать, что первые тенсегрити были созданы не людьми: паутину также можно рассматривать как тенсегрити, хотя и без жёстких частей.
Хотя геодезические купола и синергетика Фуллера принесли ему всемирную известность, большая часть математики, которую он использовал, уже хорошо зарекомендовала себя. Однако открытие его ученика Снельсона поставило действительно новые математические вопросы, которые ещё далеко не решены полностью: что такое структуры (системы) тенсегрити? Почему они устойчивы? Можно ли их классифицировать или хотя бы перечислить?
Бранко Грюнбаум, математик из Вашингтонского университета в Сиэтле, особенно ответственен за возрождение интереса математиков к таким вопросам, написав в начале 1970-х замечательный набор мимеографированных заметок под названием «Лекции по утерянной математике». В 1980 году один из нас (Коннелли) доказал гипотезу Грюмбаума, позволяющую систематически конструировать устойчивые плоские структуры тенсегрити. Но чудо и красота скульптур Снельсона, несомненно, заключаются в их трёхмерной природе, поэтому одним из мотивов нашей недавней работы было найти правильное трёхмерное обобщение. Иатематические инструменты теории групп и теории представлений в сочетании с мощными графическими и вычислительными возможностями компьютеров позволили составить полный каталог тенсегрити с определёнными заданными типами устойчивости и симметрии, в том числе такими, которые никогда раньше не наблюдались.
ЧТО ТАКОЕ ТЕНСЕГРИТИ ?
Тенсегрити отличаются чистотой и простотой, что очень естественно приводит к возможности их математического описания. Отложив в сторону физические детали конструкции, каждая тенсегрити может быть математически смоделирована как конфигурация узлов, или вершин, удовлетворяющая простым ограничениям по расстояниям. Конструкции Снельсона удерживаются вместе двумя типами конструктивных элементов (как говорят инженеры, частей), которые можно назвать тросами (кабелями) и распорками (стойками). Эти два типа элементов играют взаимодополняющие роли: тросы удерживают вершины близко друг к другу за счёт анатяжения, а распорки удерживают их на расстояиии друг от друга за счёт сжатия. При этом две вершины, соединённые кабелем, могут располагаться сколь угодно близко друг к другу (и даже находиться друг над другом, если тенсегрити упала), но они никогда не могут быть дальше друг от друга, чем длина соединяющего их кабеля. Точно так же две вершины, соединённые распоркой, никогда не могут быть ближе, чем длина распорки, но могут быть сколь угодно далеко друг от друга.
Последний пункт может поначалу показаться удивительным, потому что в большинстве настоящих тенсегрити распорки не могут быть ни длиннее, ни короче. На самом деле, для описания элемента конструкции фиксированной длины использовался термин «стержень», однако мы обнаружили, что в большинстве случаев стержни можно заменить распорками без ущерба для устойчивости (способностсь к растяжению стоек при этом сохраняется). Кроме того, концепция распорок может быть применена к другим задачам, например, таким, как упаковка сферических шаров: в любой такой упаковке центры шаров должны находиться на минимальном расстоянии друг от друга, но могут быть сколь угодно далеко друг от друга. Таким образом, тенсегрити можно рассматривать как упаковку с невидимыми распорками.
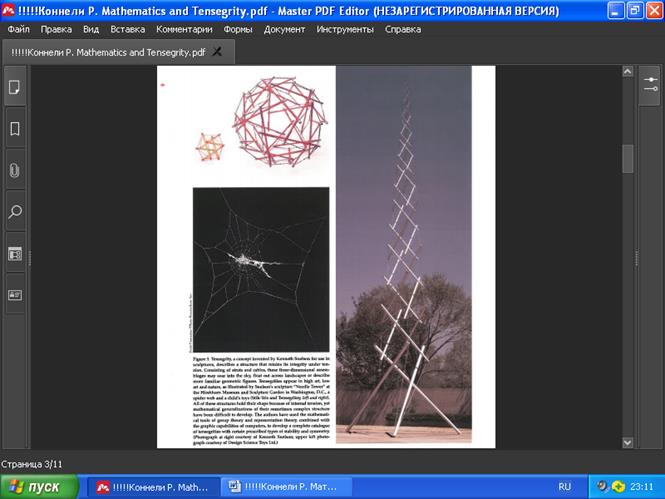
Р ИС. 1. К онцепция т енсегрити, изобрет ё нная Кеннетом Снельсоном для использования в скульптурах, описывает структур ы , котор ые восстанавлива ю т свою целостность за счёт внутренних предварительных напряжени й . Состоящие из распорок и тросов, эти трёхмерные ансамбли кажутся взмыва ющими в небо и пар ящими над ландшафтами , или могут иметь вид знакомы х геометрически х фигур. Тенсегрити широко распространены в природе от молекулярного до надорганизменного уровня (например, паутин а) и сегодня появляются как в высоком ,, так и в низком искусстве , вплоть до детски х игруш е к (Стик-Трикс и Тенсегрит и слева и справа) . Например, здесь показан а скульптур а С н ел ь сона «Игольная башня» , находящаяся в Музее Хиршхорна и в Саду скульптур в Вашингтоне, округ Колумбия. Все эти структуры сохраняют свою форму из-за внутреннего напряжения, однако математические обобщения их иногда сложной структуры было трудно разработать. Авторы использовали для этого математические аппараты теории групп и теории представлений в сочетании с графическими возможностями компьютеров для разработки полного каталога объектов с определ ё нными заданными типами устойчивости и симметрии. (Фото справа предоставлено Кеннетом Снельсоном; фото вверху слева предоставлено Design Science Toys Ltd ).
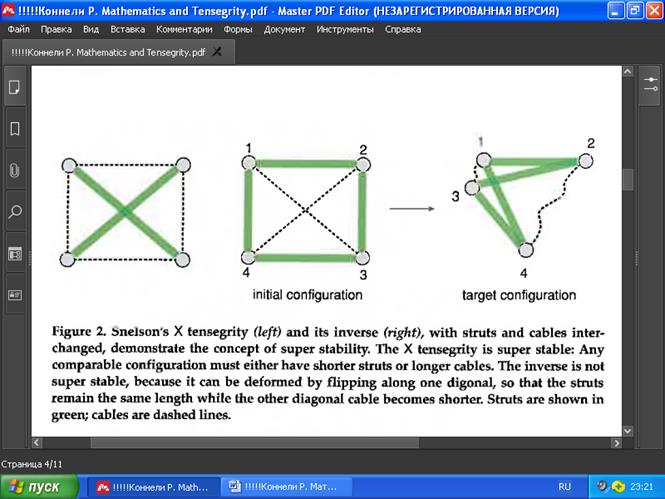
РИС. 2. Простейшая тенсегрити X-структура К.Снельсона (слева) и её инверсия при перемене мест стоек и тросов (справа) демонстрируют концепцию сверхустойчивости. Форма X-структуры очень стабильна, поскольку не может иметь более короткие стойки и более длинные тросы. Инверсия X -структуры не является устойчивой, потому что её можно деформировать, перевернув по одной диагонали при той же длине распорок, при этом другой диагональный кабель станет короче (распорки показаны зелёным цветом, тросы — пунктирными линиями).
Некоторые люди рассматривают тенсегрити как структуры, где никакие две стойки не имеют общей конечной вершины, при этом каждая вершина находится в конце стойки (то есть стойки не имеют точек касания друг с другом и как бы подвешены в пространстве на тросах). Опять же, из соображений общности мы не принимаем эти соглашения, хотя во многих упомянутых ниже примерах эти свойства имеют место.
ЧТО ТАКОЕ УСТОЙЧИВОСТЬ ?
Как и в определении самой напряжённости, существует несколько различных возможных понятий устойчивости, каждое из которых подходит лишь для определённых обстоятельств: бесконечно малая жёсткость, статическая жёсткость, жёсткость первого и второго порядка, устойчивость к предварительному напряжению и другие (определение этих понятий см. Коннелли и Уайтли, 1996). Мы выбрали очень прямое и сильное определение, название которого было предложено одним из наших студентов, Алексом Цоу. Мы можем назвать две конфигурации «сравнимыми», если они имеют одинаковое количество вершин, соединённых кабелями и распорками одинаковым образом. Цоу назвал данную тенсегрити свер х устойчивой, если любая сравнимая конфигурация вершин либо нарушает одно из ограничений по расстоянию (одна из распорок слишком короткая или один из тросов слишком длинный), либо является идентичной копией оригинала (в геометрической терминологии – конгруэнтной оригиналу).
Например, X-тенсегрити Снельсона на рис.2 является сверхустойчивой. Одним из элементарных элементов тенсегрити, который не является сверхустойчивым, является шарнир (две стойки, имеющие общую вершину): немного приоткрывая или закрывая шарнир, можно получить новую конфигурацию с той же длиной распорки, но другой формой, отличной от оригинала. Что интересно, если поменять местами тросы и распорки в X-тенсегрити, она не сможет быть сверхустойчивой даже при расположении в плоскости, хотя и является жёсткой в плоскости (в том смысле, что в неё нет непрерывного, или постепенного движения вершин, которое сохраняет ограничения длин тросов и распорок). Однако она не является жёстким в 3-мерном пространстве: подобно шарниру, её можно сгибать в новые формы, не соответствующие оригиналу.
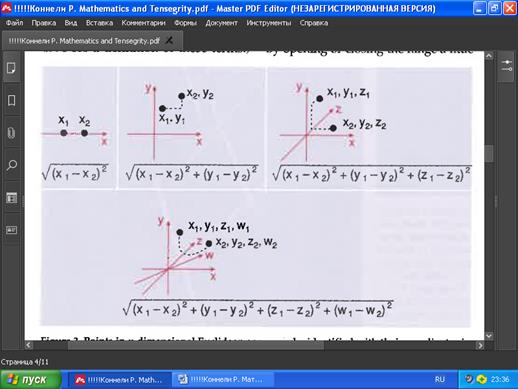
Р ИС . 3. Точки в n -мерном евклидовом пространстве можно отождествить с их координатами в декартовой системе координат , при этом к оличество координат является размерностью пространства . Расстояние в n -мерном пространстве вычисляется по аналогии с формулой Пифагора из планиметрии. Тенсегрити может быть определена в любом измерении, потому что е ё точки (узлы, вершины) и ограничения расстояни й , регулирующие положение распор о к и трос ов , могут быть указаны в терминах координат (з десь показаны примеры для 1-4-мерного пространства ) .
В отличие от просто ж ё стко й тенсегрити, сверх устойчивая тенсегрити должна исключать все возможные по структуре формы в любом количестве измерений, включая измерения 4 и выше. Математики уже привыкли к таким пространствам, так как формула Пифагора для расстояния и представление Декарта о координатах делают их такими же простыми в работе, как 2-х и 3-хмерное пространство (см. рис. 3).
ПАУТИНА И ЕЁ УСТОЙЧИВОСТЬ
Чтобы доказать, что структура тенсегити может быть устойчивой в столь сильном смысле, мы часто обращаемся к понятию, заимствованному из физики — к идее потенциальной энергии. Когда структура деформируется, она физически поглощает или отдаёт энергию. Однако математикам не нужно ограничиваться физически реалистичными энергетическими функциями, поскольку они могут изобретать удобные вымышленные энергетические функции, чтобы облегчить проверку сверхустойчивости.
Хорошей отправной точкой для понимания этих функций является самонапряжённая структура, созданная задолго до Кеннета Снельсона — паутина. Паутина отличается от обсуждавшихся до сих пор структур в двух отношениях. Во-первых, он имеет несколько «закреплённых» вершин (в пространстве или на плоскости), поэтому любая сравнимая конфигурация должна иметь вершины в точно таких же позициях. Во-вторых, в паутине есть только тросы и нет распорок (см. рис. 4).
Энергетическая функция паутины, хоть и похожа, но не идентична физической потенциальной энергии (идеальной) пружины. Как обнаружил английский Физик Роберт Гук (1635-1703), при смещении концов пружины необходимая для этого сила пропорциональна смещению из положения покоя (впоследствии он записал это эмпирическое наблюдение, известное ныне как закон Гука, в виде анаграммы «ceiinosssttun», что при расшифровке «Ut tensio, sic vis» переводится с латыни как «Какова протяжённость, такова и сила»). Хотя Гук не сформулировал свой закон в терминах энергии, он подразумевал, что энергия пружины пропорциональна квадрату расстояния, на которое она растягивается или сжимается. В паутине тенсегрити энергетическая функция одного элемента (троса или распорки) просто пропорциональна его общей длине в квадрате, как если бы элемент был пружиной с нулевой длиной покоя. Остаётся определить, каковы в структуре тенсегрити должны быть константы пропорциональности для тросов и распорок (если рассматривать их как пружины - насколько «сильны» пружины). Цель нашей задачи состоит в том, чтобы выбрать эти вымышленные «сильные» линейные элементы таким образом, чтобы структура имела единственный минимум соответствующей энергетической функции, равной сумме энергетических функций всех кабелей (при независимых внутренних силах элементов). Любая сравнимая паутина, которая не увеличивает длину кабелей, должна иметь ту же или меньшую энергию, поскольку тогда каждый кабель не может вносить больший вклад в общую сумму. Но поскольку предполагается, что данная форма структуры имеет единственыый энергетический минимум, эти две формы должны быть идентичными (конгруэнтными), а следовательно, такая паутина (которая минимизирует некоторую энергетическую функцию) сверхустойчива. Таким образом, это частное выражение принципа наименьшей работы при проектировании конструкций.
Как распознать, когда паутина имеет энергетическую функцию, которая точно минимизируется данной конфигурацией? Один из возможных ответов — равновесие напряжений — ещё одно понятие, заимствованное из инженерии. Опять же, это помогает представить тросы, которые встречаются в любой данной вершине, как пружины, каждая из которых смещена в своём направлении: как вы помните, эту силу можно сделать «сильнее» или «слабее» с помощью константы пропорциональности, которую мы назовём единичным напряжением в кабеле - таким образом, сила натяжения каждого троса равна длине, умноженной на внутреннее усилие. Если напряжения выбраны правильно, так, что «перетягивание каната» между всеми тросами, ведущими к данному услу, даёт «ничью», то напряжения в этой вершине равны и находятся в равновесии. Если это соблюдается в каждой незакреплённой вершине, то вся структура сети находится в равновесии.
Таким образом, напряжения можно задавать просто числами, которые присваиваются кабелям, поскольку они не имеют никакого отношения к размеру кабеля или даже к его физическим или механическим характеристикам. Важно только, чтобы все напряжения были положительными. Предложение: если некоторые из них равны нулю, то данная конфигурация может не иметь единственного минимума энергетической функции, и принцип наименьшей работы не будет применим. Таким образом, устойчивость состояния равновесия пока ещё неопределена, то есть равновесия напряжений недостаточно, чтобы гарантировать, что конфигурация имеет минимальную анергию. Однако для специального случая паутины без ненапряжённых кабелей этого оказыаается достаточно - причина этого в том, что функция энергии, составленная из квадратных многочленов с положительными коэффициентами, обладает свойством, называемым выпуклостью: как бы вы ни двигали {незакреплённые) вершины, начиная с критической равновесной конфигурации, энергетическая функция структуры увеличится; то есть в ыпуклая функция, как и парабола, может иметь только один минимум. Поэтому, если (напряжённая) паутина удовлетворяет условию равновесия, оно должно быть единственным. Таким образом, для паутины пригоден принцип наименьшей работы и она сверх устойчива.
Обратите внимание, что этот метод (выпуклость) не просто даёт «локальный» результат, действительный только для малых или ограниченных возмущений в паутине - он работает и для любой другой конфигурации, которую можно представить в любом многомерном евклидовом пространстве. Поэтому пауки не могут испортить свою плоскую паутину мухами даже в более высоких измерениях.
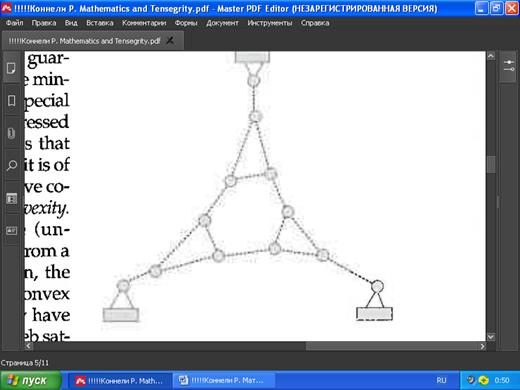
РИС. 4. Математическая паутина состоит только из тросов, без распорок. Три вершины закреплены (заштрихованные прямоугольники) и не могут двигаться относительно фона. Чтобы сеть была сверхустойчивой, идущие от закреплённых вершин три кабеля должны определять линии, проходящие только через одну точку.

Р ИС. 5. К аффинным преобразованиям относятся растяжения (а), повороты (б) и проекции (в). Все эти преобразования обладают тем свойством, что равновесное напряжение для исходной тенсегрити также служит равновесным напряжением для преобразованной тенсегрити (о братите внимание, что выступ ы и конечные размеры мо гут прив оди т ь к пере сечению-контактам распорок и тросов ) .
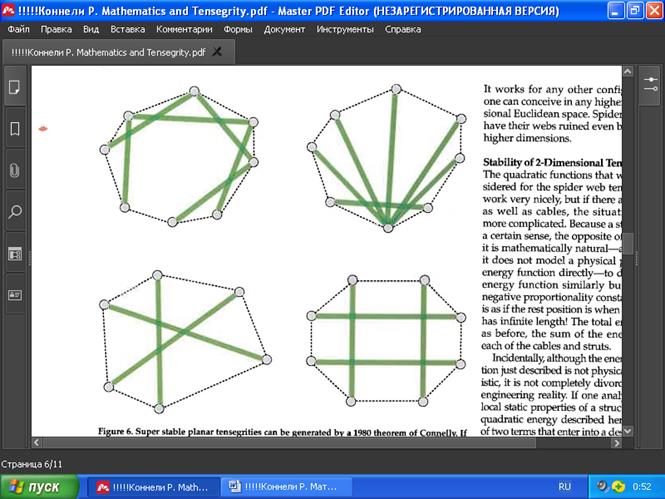
Р ИС. 6. Сверх устойчивые плоские тенсегрити могут быть получены с помощью теоремы Коннелли 1980 года : Если тросы образуют строго выпуклый многоугольник, распорки расположены по внутренней диагонали и кажд ый трос имеет положительное напряжение, кажд ая распорк а - отрицательное напряжение и соблюдается равновесие в каждой вершине, то тенсегрити сверх устойчива . Причём с табильность не всегда интуитивно очевидна. Конфигурация, вдохновленная теоремой о ж ё сткости, доказанной французским математиком Огюстеном Лулем Коши в 1813 году, показана вверху слева. Пример структуры класса, предложенного Бранко Гр ю мбаумом из Вашингтонского университета - вверху справа. Конфигурация, которая является сверхустойчивой только , если все вершины лежат на эллипсе - внизу слева.








