Изучение процессов зарядки и разрядки конденсатора. Лабораторная работа
Цель:
- изучить принцип работы платформы Лукас Нулле (LN)
- определение ёмкости конденсатора.
Оборудование:
1. Экспериментер ПАК LN
2. Набор элементов «Базовые схемы постоянного тока»
(резистор 47 кОм, конденсатор емкостью 470 мкФ )
3. Панель питания ПАК LN
4. Источник питания (220В)
5. Ключ-кнопка
6. Мультиметр
7. Секундомер
Теоретическое введение
Конденсатором называется система проводников (обкладок), разделенных диэлектриком. Обкладки заряженного конденсатора имеют равные по величине и противоположные по знаку заряды 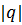 . Форма и размеры обкладок должны быть такими, чтобы электрическое поле было сосредоточено между ними. В зависимости от формы обкладок конденсатор может быть плоским, цилиндрическим, сферическим (рис. 1).
. Форма и размеры обкладок должны быть такими, чтобы электрическое поле было сосредоточено между ними. В зависимости от формы обкладок конденсатор может быть плоским, цилиндрическим, сферическим (рис. 1).
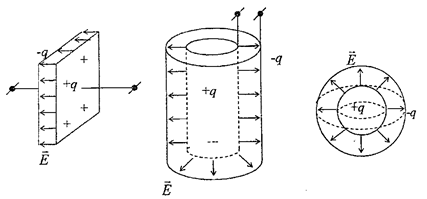
Рис. 1
Электроемкостью конденсатора C называется коэффициент пропорциональности между зарядом обкладок q и разностью потенциалов между ними 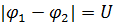 ,
,
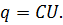 (1)
(1)
Это физическая величина, численно равная заряду, который надо сообщить обкладкам, чтобы разность потенциалов между ними увеличилась на 1 В.
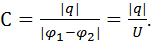 (2)
(2)
Единица измерения емкости – фарад (Ф). Емкость не зависит ни от заряда, ни от разности потенциалов (при увеличении q пропорционально увеличивается U), а определяется формой, и размерами обкладок, и свойствами диэлектрика между ними.
Электроемкость плоского конденсатора рассчитывается по формуле
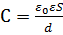 (3)
(3)
где S – площадь обкладок, d – расстояние между ними, 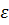 – диэлектрическая проницаемость диэлектрика, заполняющего конденсатор,
– диэлектрическая проницаемость диэлектрика, заполняющего конденсатор, 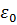 – электрическая постоянная.
– электрическая постоянная.
Конденсаторы можно соединять в батарею разными способами.

Рис. 2
При параллельном соединении (рис. 2) эквивалентная емкость батареи
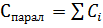 (4)
(4)
При этом разность потенциалов на всех конденсаторах одинакова, а общий заряд равен сумме зарядов конденсаторов.
При последовательном соединении конденсаторов электроемкость батареи определяется соотношением
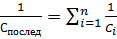 (5)
(5)
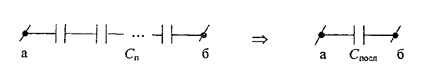
Рис. 3
Заряды всех конденсаторов при этом одинаковы, а разность потенциалов на клеммах батареи 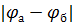 равна сумме разностей потенциалов на каждом конденсаторе.
равна сумме разностей потенциалов на каждом конденсаторе.
Описание установки

Рис. 4
На рисунке 4 изображена схема, подключенная к экспериментеру ПАК LN.
Элементы схемы:
1 – мультиметр,
2 – ключ-кнопка,
3 – ключ,
4 – сопротивление,
5 – конденсатор.
Схематичное изображение электрической цепи показано на рисунке 5.
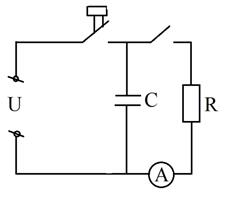
Рис. 5
Когда ключ-кнопка находится в нажатом положении, конденсатор подключается к источнику питания. Происходит зарядка конденсатора до разности потенциалов U=5 В. После окончания зарядки – отпускаем кнопку. Когда ключ замыкает цепь, обкладки заряженного конденсатора подключаются к резистору R. Под действием кулоновских сил заряд с одной обкладки конденсатора переходит на другую через резистор, при этом ток фиксируется мультиметром.
При разрядке конденсатора сила тока разрядки постепенно уменьшается, как на рисунке 6.
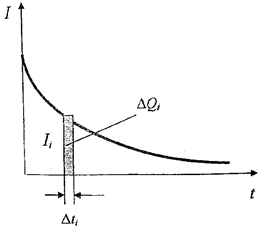
Рис. 6
По определению сила тока равна заряду, прошедшему через сечение проводника за единицу времени. Тогда заряд 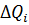 , прошедший за
, прошедший за 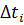 , определяется формулой
, определяется формулой
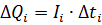 , (6)
, (6)
что графически равно площади прямоугольника, заштрихованного на рисунке 6. Весь заряд Q, который был на обкладках конденсатора до начала разрядки, равен площади криволинейной фигуры, ограниченной линией графика и осями координат.
Ход работы
1. Визуально ознакомьтесь с установкой, заполните таблицу спецификации измерительных приборов.
Таблица №1. Спецификация измерительных приборов.
| № п/п | Наименование прибора | Предел измерения | Цена деления | Приборная погрешность |
| 1. | Микроамперметр | |||
| 2. | секундомер |
Рабочее напряжение U=5.0 В , ΔU=0.1 В
2. В течение 10 секунд заряжайте конденсатор, нажимая на кнопку-ключ. Отпустите кнопку-ключ.
3. Подготовьте секундомер. Одновременно с замыканием ключа включите секундомер. Каждые 10 секунд фиксируйте значение тока с помощью микроамперметра и заносите их в таблицу №2.
Таблица №2. Зависимость тока разрядки от времени
| № п/п | t, c | I, A |
| 1. | ||
| 2. | ||
| 3. | ||
| … | ||
| n |
Обработка результатов измерений
1. По данным таблицы №2 на миллиметровой бумаге постройте график зависимости тока разрядки конденсатора от времени.
2. Найдите весь заряд Q, который был на обкладках конденсатора до начала разрядки с помощью метода подробно описанного перед ходом работы.
3. Вычислите ёмкость конденсатора по формуле (2).
Расчет погрешностей
1. Так как измерение проводилось один раз, случайной погрешностью можно пренебречь. Справедлива следующая формула:
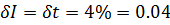
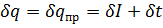 (7)
(7)
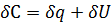 (8)
(8)
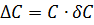 (9)
(9)
2. Запишите результат измерения емкости С в виде доверительного интервала.
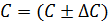 (единицы измерения) (10)
(единицы измерения) (10)
Выводы
- Сравните экспериментально полученное значение емкости конденсатора с теоретическим значением
- Сделайте выводы о характере изменения силы тока при разрядке конденсатора, дайте объяснение
- что изменится, если конденсатор заменить другим с меньшей емкостью?
- что изменится, если к имеющемуся конденсатору подключить еще один такой же конденсатор
А) последовательно
Б) параллельно








